Trong không gian tọa độ Oxyz cho hai điểm A(1; -1; 2), B(2; 0; 1)

Ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 10 trang 124 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 10 (trang 124 sgk Hình Học 12 nâng cao): Trong không gian tọa độ Oxyz cho hai điểm A(1; -1; 2), B(2; 0; 1)

a) Tìm quỹ tích các điểm M sao cho: MA²-MB²=2

b) Tìm quỹ tích các điểm N sao cho NA²+NB²=3

c) Tìm quỹ tích các điểm cách đều hai mặt phẳng (OAB) và (Oxy)

Lời giải:

a) Giả sử M(x, y, z) là điểm thỏa mãn MA²-MB²=2 (*)

Khi đó (*) <=> (x-1)²+(y+1)²+(z-2)²-(x-2)²-y²-(z-1)²=2

<=> 2x+2y-2z-1=0 (α). Vậy quỹ tích M là mặt phẳng (α).

b) Gọi N(x, y, z) là điểm thỏa mãn NA²+NB²=3 (**)

Khi đó, (**) <=> (x-1)²+(y+1)²+(z-2)²+(x-2)²+y²+(z-1)²=3

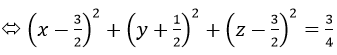
Vậy quỹ tích điểm N là mặt cầu tâm

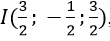
và có bán kính R = √3/2.

c) Gọi điểm P(x, y, z) là điểm cách đều hai mặt phẳng: (OAB) và (Oxy), khi đó ta có: d(P, OAB)) = d(P, (Oxy)) (***)

Mặt phẳng (OAB) có Phương trình là: -x+3y+2z=0

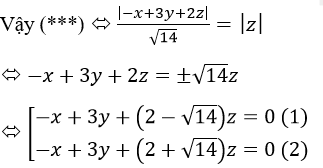
Vậy quỹ tích các điểm P thỏa mãn bài toán là hai mặt phẳng lần lượt là (1) và (2).