Cho mặt phẳng (P): mx+y+(n-2)z+m+2=0. Với mọi m, n mặt phẳng (P) đi qua điểm cố định

Ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 22 trang 128 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 22 (trang 128 sgk Hình Học 12 nâng cao): Cho mặt phẳng (P): mx+y+(n-2)z+m+2=0. Với mọi m, n mặt phẳng (P) đi qua điểm cố định:

A. (1; 2; 0)    B. (2; 1; 0)     C. (0; 1; -2)     D. (-1; -2; 0)

Lời giải:

Gọi M₀(x₀,y₀,z₀) là điểm cố định của mp(P)

Khi đó: mx₀+y₀+(n-2) z₀+m+2=0 đúng với ∀m,n

<=> m(x₀+1)+y₀+nz_0-2z₀+2=0 đúng với ∀m,n

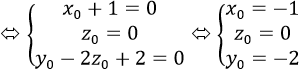
=> M₀(-1;-2;0)

Vậy chọn D