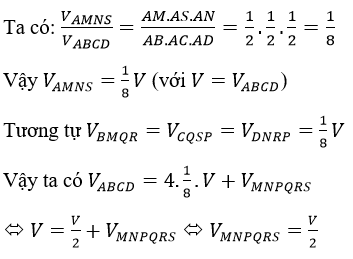Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình 8 mặt đều

Ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 4 trang 122 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 4 (trang 122 sgk Hình Học 12 nâng cao): Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình 8 mặt đều. Hãy so sánh tứ diện đều đã cho và thể tích của hình 8 mặt đều đó.

Lời giải:

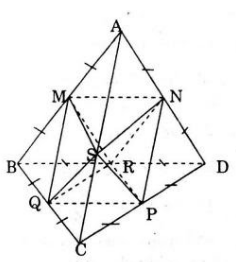
Cho tứ diện ABCD gọi M, N, P,Q, R, S lần lượt là trung điểm của 6 cạnh AB, AD, BD, BC, CD, BC của tứ diện, khi đó khối đa diện MNPQRS là một hình tám mặt.

Xét tam giác ABC có M và S lần lượt là trung điểm của AB và AC nên MS là đường trung bình của tam giác ABC

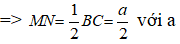
Chứng minh tương tự ta được: MN = MR = NR = NP =NS = SP = QM = QS = MS = QP = a/2 với a là cạnh tứ diện nên MNPQRS là một hình tám mặt đều.

Khi đó khối đa diện MNPQRS là một hình tám mặt.