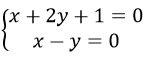Trong không gian tọa độ Oxyz, cho đường thẳng Δ có phương trình

Ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 9 trang 123 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 9 (trang 123 sgk Hình Học 12 nâng cao): Trong không gian tọa độ Oxyz, cho đường thẳng Δ có phương trình

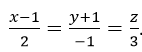
a) Viết phương trình hình chiếu của Δ trên các mặt phẳng tọa độ.

b) Chứng minh rằng mặt phẳng: x+5y+z+4=0 đi qua Δ.

c) Tính khoảng cách giữa đường thẳng Δ và các trục tọa độ.

d) Viết phương trình đường vuông góc chung của Δ và đường thẳng Δ':x=y=z

e) Viết phương trình đường thẳng song song với Oz, cắt cả ∆ và ∆’.

Lời giải:

a) Mặt phẳng chứa Δ và vuông góc với mp(Oxy) có phương trình là:

x+2y+1=0

Vậy hình chiếu vuông góc của Δ lên mp(Oxy) có phương trình là:

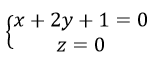
Tương tự, hình chiếu vuông góc của Δ lên mp()yz) và (Oxz) có phương trình là:

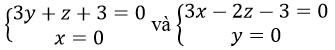
b) Δ đi qua M₀ (1; -1;0) và có vectơ pháp tuyến u→=2;-1; 3 ta thấy:

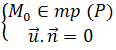
suy ra Δ nằm trên mp: x+5y+z+4=0

Cách khác: ta thấy tọa độ 2 điểm M₀ (1; -1;0) và M₁ (3; -2;3) thõa mãn phương trình mp: x+5y+z+4=0 nên Δ thuộc mặt phẳng đã cho.

c) Khoảng cách giữa Δ và trục Ox được xác định như sau:

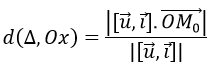
Trong đó u→=(2; -1;3) là vectơ chỉ phương của Δ

i→=(1;0;0)là vectơ chỉ phương của Ox.

M₀ (1; -1;0) ∈Δ,O(0;0;0) là gốc tọa dộ.

Ta có [uX→,i→]=(0;3;1),OM₀→=(1; -1;0)

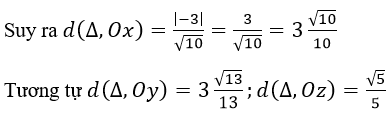
d) Đường thẳng Δ đi qua M₀ (1; -1;0) có vectơ chỉ phương u→=(2; -1;3)

Δ' đi qua M₀'(0;0;0) có vectơ chỉ phương u'→=(1;1;1)

Gọi d là đường vuông góc chung của ∆ và ∆’.

Giả sử d cắt ∆, ∆’ lần lượt tại A(1+ 2a, -1- a,3a) và B( b, b,b)

⇒ AB→(b-1- 2a, b+1+ a, b- 3a)

Do d vuông góc với ∆ và ∆’ nên ta có:

e) Đường thẳng cần tìm là giao tuyến của (α) và (β); trong đó, (α) là mặt phẳng chứa Δ và (α) song song với Oz.

(β) là mặt phẳng chứa Δ' và (β) song song với Oz.

Phương trình của (α) là: x+2y+1=0

Phương trình của (β) là: x-y=0

Suy ra Phương trình đường thẳng cần tìm là: