Cho hình trụ có bán kính R và đường cao R√2. Gọi AB và CD là hai đường kính thay đổi của hai đường tròn

Ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 7 trang 123 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 7 (trang 123 sgk Hình Học 12 nâng cao): Cho hình trụ có bán kính R và đường cao R√2. Gọi AB và CD là hai đường kính thay đổi của hai đường tròn đáy mà AB vuông góc với CD.

a) Chứng minh rằng ABCD là tứ diện đều.

b) Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với một mặt trụ cố định (tức là khoảng cách từ các đường thẳng đó tới trục của mặt trụ bán kính mặt trụ).

Lời giải:

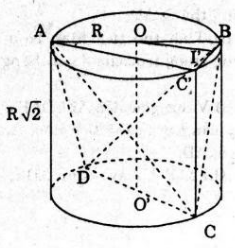
a) Vì AB ⊥ CD nên ta chứng minh được ΔDBC cân tại B, suy ra BD = BC, tương tự ta có: AC=AD=BD=BC

Trong tam giác vuông OO’C có: BC²=O'B²+O'C²

Trong tam giác vuông O’OB có: O'B²=O'O²+OB²

Vậy BC²=O'O²+OB²+O'C²

= (R√2 )²+R²+R²=4R²

BC = 2R. vậy tứ diện ABCD có 6 cạnh bằng nhau và bằng 2R nên nó là tứ diện đều. (đpcm).

b) Kẻ đường sinh CC’ của hình trụ.

Ta có mp(C’BC) // OO’

Suy ra khoảng cách giữa OO’ và BC bằng khoảng cách từ OO’ đến mp(C’BC) và bằng OI (I là trung điểm BC’)

Ta tính được OI = R√2/2 (trong tam giác vuông AC’B cân tại C’)

Tương tự, khoảng cách giữa các đường thẳng AC, AD, BC, BD luôn tiếp xúc với mặt trụ có trục là đường thẳng OO’ và có bán kính là R√2/2.