Mệnh đề toán học (Lý thuyết Toán lớp 10) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 1: Mệnh đề toán học sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Mệnh đề toán học (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Mệnh đề toán học

1. Mệnh đề toán học

• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.

Ví dụ:

+ “Hà Nội là thủ đô của Việt Nam” không phải một sự kiện toán học. Do đó khẳng định này không phải mệnh đề toán học.

+ “Số π là một số hữu tỉ” là khẳng định một sự kiện trong toán học. Do đó khẳng định này là một mệnh đề toán học.

• Mỗi mệnh đề toán học phải đúng hoặc sai, không thể vừa đúng, vừa sai.

- Khi mệnh đề toán học là đúng, ta gọi mệnh đề đó là một mệnh đề đúng.

- Khi mệnh đề toán học là sai, ta gọi mệnh đề đó là một mệnh đề sai.

Ví dụ:

+ “Tổng ba góc trong tam giác bằng 180⁰” là một mệnh đề đúng.

+ “ $\sqrt{2}$ là số hữu tỉ” là một mệnh đề sai (vì $\sqrt{2}\approx 1,\mathrm{414213562...}$ là một số vô tỉ).

2. Mệnh đề chứa biến

• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.

Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …

Ví dụ:

+ P(x): “x là một số nguyên tố” là một mệnh đề chứa biến

Với x = 3, mệnh đề P(x): “3 là một số nguyên tố” là mệnh đề đúng.

Với x = 8, mệnh đề P(x): “8 là một số nguyên tố” là mệnh đề sai.

3. Phủ định của một mệnh đề

• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là $\overline{P}$.

Mệnh đề $\overline{P}$ đúng khi P sai, và ngược lại.

Ví dụ:

+ A: “69420 là một số lẻ” là mệnh đề sai.

Mệnh đề phủ định $\overline{A}$: “69420 không phải một số lẻ”, $\overline{A}$ là mệnh đề đúng.

Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.

4. Mệnh đề kéo theo

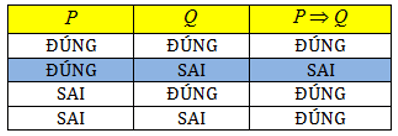
• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.

Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.

Nhận xét: Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…

Ví dụ:

+ Xét hai mệnh đề: P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi”.

+ Mệnh đề P ⇒ Q được phát biểu là: “Nếu tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi”. Mệnh đề này là mệnh đề đúng.

 

Nhận xét: Các định lí toán học thường phát biểu ở dạng mệnh đề kéo theo P ⇒ Q.

Khi đó ta nói:

P là giả thiết, Q là kết luận của định lí, hay P là điều kiện đủ để có Q, hoặc Q là điều kiện cần để có P.

Ví dụ:

Ta có định lý: Nếu một tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰ thì tứ giác đó nội tiếp được đường tròn.

Khi đó, ta nói:

+ Tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰ là điều kiện đủ để tứ giác đó nội tiếp được đường tròn.

+ Tứ giác đó nội tiếp được đường tròn là điều kiện cần để tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰.

5. Mệnh đề đảo. Mệnh đề tương đương

• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.

Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.

Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:

+ “P tương đương Q”;

+ “P là điều kiện cần và đủ để có Q”;

+ “P khi và chỉ khi Q”;

+ “P nếu và chỉ nếu Q”.

Ví dụ: Với P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi” thì P ⇒ Q: “Tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi” là mệnh đề đúng, và Q ⇒ P: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD có bốn cạnh bằng nhau” cũng là mệnh đề đúng.

Do đó P ⇔ Q, phát biểu:

+ “Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD có bốn cạnh bằng nhau”.

+ “Tứ giác ABCD là hình thoi là điều kiện cần và đủ để tứ giác ABCD có bốn cạnh bằng nhau”.

Chú ý: Trong toán học, những câu khẳng đỉnh đúng phát biểu ở dạng “P ⇔ Q” cũng được coi là một mệnh đề toán học, gọi là mệnh đề tương đương.

6. Kí hiệu ∀ và ∃

• Kí hiệu ∀ đọc là “với mọi”.

• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).

Ví dụ: Phát biểu các mệnh đề:

+ “$\forall x\in ℝ,x^2+1>0$”: Với mọi số thực x thì x² + 1 luôn lớn hơn 0.

+ “$\exists x\in \mathbb{N},2x=3$”: Tồn tại số tự nhiên x sao cho 2x bằng 3.

• Phủ định của mệnh đề “$\forall x\in X,P\left(x\right)$” là mệnh đề “$\exists x\in X,\overline{P\left(x\right)}$”.

• Phủ định của mệnh đề “$\exists x\in X,P\left(x\right)$” là mệnh đề “$\forall x\in X,\overline{P\left(x\right)}$”.

Ví dụ:

+ Phủ định của mệnh đề “$\forall x\in ℝ,x^2+1>0$” là mệnh đề “$\exists x\in ℝ,x^2+1\le 0$”.

+ Phủ định của mệnh đề “$\exists x\in \mathbb{N},2x=3$” là mệnh đề “$\forall x\in \mathbb{N},2x\ne 3$”.

Bài tập Mệnh đề toán học

Bài 1. Trong các câu sau, câu nào là mệnh đề chứa biến:

A. 1 + 1 = 3          

B. 4 + x < 3

C. 2,3 có phải một số nguyên không? 

D. π là một số hữu tỉ

Hướng dẫn giải:

Đáp án đúng là: B

“4 + x < 3” là mệnh đề có chứa biến x.

“1 + 1 = 3” và “π là một số hữu tỉ” là các mệnh đề không chứa biến.

“2,3 có phải một số nguyên không?” là một câu hỏi, không phải mệnh đề.

Bài 2. Phát biểu phủ định của mệnh đề sau và xét tính đúng sai của nó:

a) P: “15 không chia hết cho 3”

b) Q: “$\sqrt{2}>1$”

Hướng dẫn giải:

a) Mệnh đề phủ định của mệnh đề P là $\overline{P}$: “15 chia hết cho 3”.

Vì 15 = 3.5 nên 15 chia hết cho 3. Do đó $\overline{P}$ là mệnh đề đúng.

b) Mệnh đề phủ định của mệnh đề Q là $\overline{Q}$: “$\sqrt{2}\le 1$”.

Vì $\sqrt{2}\approx 1,41$ > 1 nên $\overline{Q}$  là mệnh đề sai.

Bài 3. Xét các mệnh đề P: “x là một số hữu tỉ” và Q: “x² là một số hữu tỉ”.

a) Phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của nó.

b) Phát biểu mệnh đề đảo của mệnh đề trên.

c) Chỉ ra một giá trị của x mà mệnh đề đảo sai.

Hướng dẫn giải:

a) Mệnh đề P ⇒ Q được phát biểu là: “Nếu x là một số hữu tỉ thì x² là một số hữu tỉ”.

Mệnh đề P ⇒ Q là mệnh đề đúng.

b) Mệnh đề đảo Q ⇒ P: “Nếu x² là một số hữu tỉ thì x là một số hữu tỉ”.

c) Ta thấy nếu x² = 3 thì $x=\sqrt{3}$ không phải một số hữu tỉ.

Bài 4. Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng sai của chúng:

a) P(x): “$\forall x\in ℝ,x^2>0$” b) Q(n): “$\exists n\in \mathbb{N},2n+5<2$”

Hướng dẫn giải:

a) Mệnh đề phủ định $\overline{P\left(x\right)}:"\exists x\in ℝ,x^2\le 0"$.

Do tồn tại giá trị x = 0 thoả mãn x² ≤ 0, nên $\overline{P\left(x\right)}$ là mệnh đề đúng.

b) Mệnh đề phủ định $\overline{Q\left(n\right)}:"\forall n\in \mathbb{N},2n+5\ge 2"$.

Vì n ∈ ℕ nên n ≥ 0

⇒ 2n + 5 ≥ 5 > 2.

Do đó $\overline{Q\left(n\right)}$ là mệnh đề đúng.

Học tốt Mệnh đề toán học

Các bài học để học tốt Mệnh đề toán học Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài 1: Mệnh đề toán học