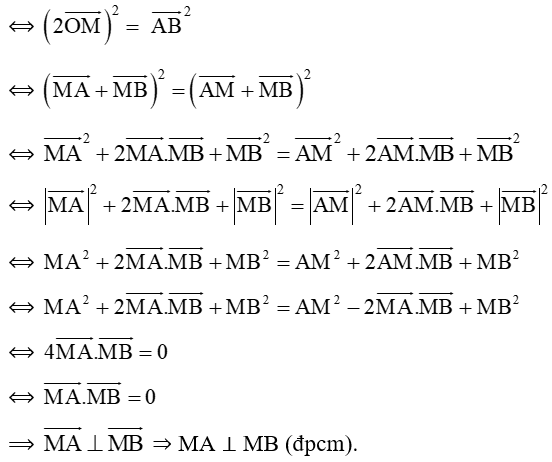Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

❮ Bài trước Bài sau ❯

Với Tổng hợp lý thuyết Toán 10 Chương 4: Hệ thức lượng trong tam giác. Vectơ sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Trắc nghiệm tổng hợp Toán 10 Chương 4 (có đáp án)

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Lý thuyết tổng hợp Toán 10 Chương 4

1. Giá trị lượng giác của một góc từ 0° đến 180°

1.1 Định nghĩa

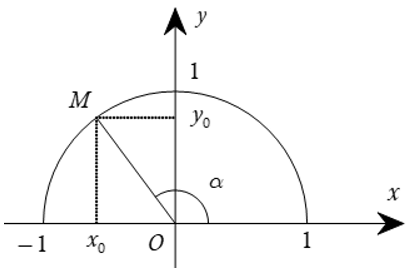
Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Với mỗi góc α (0≤α≤180°) ta xác định một điểm M (x₀, y₀) trên nửa đường tròn đơn vị sao cho góc $\hat{x O M}$ =α.Khi đó ta có định nghĩa:

+) sin của góc α, kí hiệu là sinα, được xác định bởi: sinα = y₀;

+) côsin của góc α, kí hiệu là cosα, được xác định bởi: cosα = x₀;

+) tang của góc α, kí hiệu là tanα, được xác định bởi: tanα = $\frac{y_{0}}{x_{0}}$ (x₀ ≠ 0);

+) côtang của góc α, kí hiệu là cotα, được xác định bởi: cotα = $\frac{x_{0}}{y_{0}}$ (y₀ ≠ 0).

Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.

Chú ý:

tanα = $\frac{\sin α}{\cos α}$ (α ≠ 90°);

cotα = $\frac{\cos α}{\sin α}$ (0 < α < 180°).

sin(90° - α) = cosα (0° ≤ α ≤ 90°);

cos(90° - α) = sinα (0° ≤ α ≤ 90°);

tan(90° - α) = cotα (0° ≤ α ≤ 90°);

cot(90° - α) = tanα (0° ≤ α ≤ 90°).

1.2. Tính chất

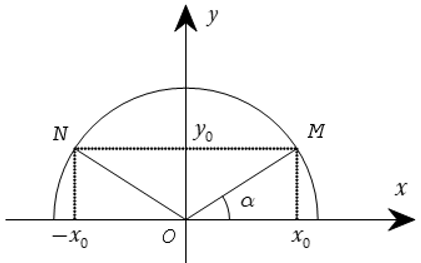
Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Trên hình bên ta có dây cung NM song song với trục Ox và nếu $\hat{x O M}$ = α thì $\hat{x O N}$ = 180^o – α. Với 0° ≤ α ≤ 180° thì:

sin(180° - α) = sinα,

cos(180° - α) = - cosα,

tan(180° - α) = - tanα (α ≠ 90°),

cot(180° - α) = - cotα (α ≠ 0°, α ≠ 180°).

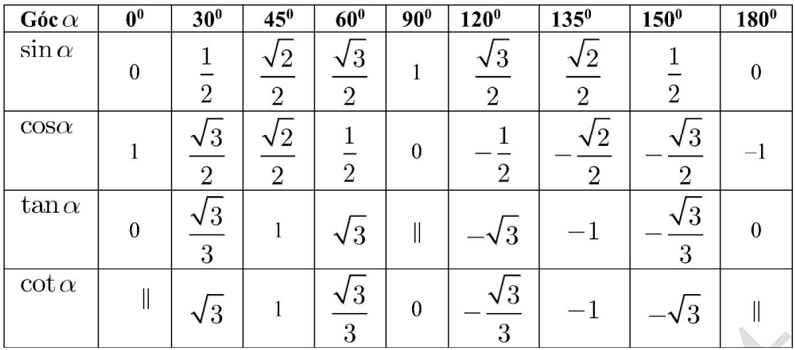
1.3. Giá trị lượng giác của các góc đặc biệt

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Chú ý: Cách sử dụng máy tính cầm tay để tính giá trị lượng giác:

- Ta có thể tìm giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng cách sử dụng các phím: sin, cos, tan trên máy tính cầm tay.

2. Định lí côsin

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:

a² = b² + c² – 2bccosA,

b² = c² + a² – 2cacosB,

c²= a² + b² – 2abcosC.

Lưu ý:

cosA = $\frac{b^{2} + c^{2} - a^{2}}{2 b c}$ ,

cosB = $\frac{c^{2} + a^{2} - b^{2}}{2 c a}$ ,

cosC = $\frac{a^{2} + b^{2} - c^{2}}{2 a b}$ .

3. Định lí sin

Cho tam giác ABC có BC = a, CA = b, AB = c và bán kính đường tròn ngoại tiếp là R. Khi đó:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

Lưu ý:

a = 2RsinA,

b = 2RsinB,

c = 2RsinC.

4. Tính diện tích tam giác

Công thức tính diện tích tam giác:

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:

S = $\frac{1}{2}$ bc.sinA = $\frac{1}{2}$ ca.sinB = $\frac{1}{2}$ ab.sinC

Công thức Heron:

Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, $p = \frac{a + b + c}{2}$ . Khi đó, diện tích S của tam giác ABC là:

$S = \sqrt{p (p - a) (p - b) (p - c)}$ .

Trong đó p là nửa chu vi tam giác ABC.

5. Vectơ

Định nghĩa: Vectơ là một đoạn thẳng có hướng.

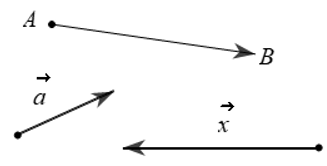
Vectơ có điểm đầu A, điểm cuối B được kí hiệu là $\vec{A B}$ và đọc là “vectơ AB”. Để vẽ được vectơ $\vec{A B}$ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Đối với vectơ $\vec{A B}$ , ta gọi:

- Đường thẳng d đi qua hai điểm A và B là giá của vectơ $\vec{A B}$ .

- Độ dài đoạn thẳng AB là độ dài của vectơ $\vec{A B}$ , kí hiệu là | $\vec{A B}$ |.

Vectơ còn được kí hiệu là $\vec{a}$ , $\vec{b}$ , $\vec{x}$ , $\vec{y}$ khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Độ dài của vectơ được kí hiệu là | $\vec{a}$ |

Ví dụ: Vectơ $\vec{A B}$ có độ dài là 5, ta có thể viết như sau: | $\vec{A B}$ | = 5.

6. Vectơ cùng phương, vectơ cùng hướng

Định nghĩa:

- Hai vectơ cùng phương: Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

- Hai vecto cùng phương có thể cùng hướng hoặc ngược hướng.

7. Hai vectơ bằng nhau

Hai vectơ $\vec{A B}$ , $\vec{C D}$ bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: $\vec{a} = \vec{b}$

Nhận xét:

- Hai vectơ $\vec{a}$ và $\vec{b}$ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu $\vec{a} = \vec{b}$ .

- Khi cho trước vectơ $\vec{a}$ và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho $\vec{O A}$ = $\vec{a}$ .

8. Vectơ-không

Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.

Bây giờ với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là $\vec{A A}$ và được gọi là vectơ – không.

Định nghĩa: Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là $\vec{0}$ .

Ta quy ước $\vec{0}$ cùng phương và cùng hướng với mọi vectơ và | $\vec{0}$ |= 0.

Nhận xét: Hai điểm A, B trùng nhau khi và chỉ khi $\vec{A B}$ = $\vec{0}$ .

9. Tổng của hai vectơ

9.1. Định nghĩa

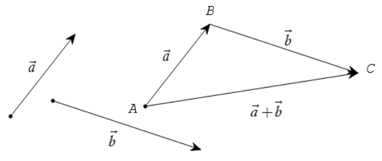
- Với ba điểm bất kì A, B, C, vectơ $\vec{A C}$ được gọi là tổng của hai vectơ $\vec{A B}$ và $\vec{B C}$ , kí hiệu là $\vec{A C} = \vec{A B} + \vec{B C}$ .

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Phép lấy tổng của hai vectơ còn được gọi là phép cộng vectơ.

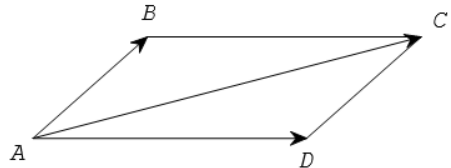
9.2. Quy tắc hình bình hành

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Nếu ABCD là hình bình hành thì $\vec{A B} + \vec{A D} = \vec{A C}$ .

9.3. Tính chất

Với ba vecto tùy ý $\vec{a}, \vec{b}, \vec{c}$ ta có:

$\vec{a} + \vec{b} = \vec{b} + \vec{a}$ (tính chất giao hoán) ;

$(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$ (tính chất kết hợp);

$\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$ (tính chất của vecto-không).

Chú ý: Tổng ba vecto $\vec{a} + \vec{b} + \vec{c}$ được xác định theo một trong hai cách sau:

$(\vec{a} + \vec{b}) + \vec{c}$ hoặc $\vec{a} + (\vec{b} + \vec{c})$ .

10. Hiệu của hai vectơ

10.1. Hai vectơ đối nhau

Định nghĩa: Vectơ có cùng độ dài và ngược hướng với vectơ $\vec{a}$ được gọi là vectơ đối của vectơ $\vec{a}$ , kí hiệu là - $\vec{a}$ . Hai vectơ $\vec{a}$ và - $\vec{a}$ được gọi là hai vectơ đối nhau.

Quy ước: Vectơ đối của vectơ $\vec{0}$ là vectơ $\vec{0}$ .

Nhận xét:

+) $\vec{a} + (- \vec{a}) = (- \vec{a}) + \vec{a} = \vec{0}$

+) Hai vecto $\vec{a}$ , $\vec{b}$ là hai vecto đối nhau khi và chỉ khi $\vec{a} + \vec{b} = \vec{0}$ .

+) Với hai điểm A, B, ta có: $\vec{A B} + \vec{B A} = \vec{0}$ .

Lưu ý: Cho hai điểm A, B. Khi đó hai vectơ $\vec{A B}$ và $\vec{B A}$ là hai vectơ đối nhau, tức là $\vec{B A} = - \vec{A B}$ .

Chú ý:

- I là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{I A} + \vec{I B} = \vec{0}$ .

- G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

10.2. Hiệu của hai vectơ

Hiệu của hai vecto $\vec{a}$ và $\vec{b}$ , kí hiệu là $\vec{a} - \vec{b}$ , là tổng của vecto $\vec{a}$ và vecto đối của vecto $\vec{b}$ , tức là $\vec{a} - \vec{b} = \vec{a} + (- \vec{b})$ .

Phép lấy hiệu của hai vecto được gọi là phép trừ hai vecto.

Nhận xét: Với ba điểm bất kì A, B, O ta có: $\vec{A B} = \vec{O B} - \vec{O A}$ .

11. Tích của vecto với một số

Cho một số k ≠ 0 và vectơ $\vec{a}$ ≠ $\vec{0}$ . Tích của một số k với vectơ $\vec{a}$ là một vectơ, kí hiệu là $k \vec{a}$ , được xác định như sau:

+ cùng hướng với $\vec{a}$ nếu k > 0, ngược hướng với $\vec{a}$ nếu k < 0;

+ có độ dài bằng |k|.| $\vec{a}$ |.

Quy ước: $0 \vec{a} = \vec{0}, k \vec{0} = \vec{0}$ .

Phép lấy tích của một số với một vecto gọi là phép nhân một số với một vecto.

Tính chất

Với hai vecto bất kì $\vec{a}$ , $\vec{b}$ và hai số thực h, k, ta có:

+) k( $\vec{a} + \vec{b}$ ) = k $\vec{a}$ + k $\vec{b}$ ; k( $\vec{a} - \vec{b}$ ) = k $\vec{a}$ - k $\vec{b}$ ;

+) (h + k) $\vec{a}$ = h $\vec{a}$ + k $\vec{a}$ ;

+) h(k $\vec{a}$ ) = (hk) $\vec{a}$ ;

+) 1 $\vec{a}$ = $\vec{a}$ ; (-1) $\vec{a}$ = - $\vec{a}$ .

Nhận xét: k $\vec{a}$ = $\vec{0}$ khi và chỉ khi k = 0 hoặc $\vec{a} = \vec{0}$ .

- Nếu I là trung điểm của đoạn thẳng AB thì $\vec{M A} + \vec{M B} = 2 \vec{M I}$ với điểm M bất kì.

- Nếu G là trọng tâm của tam giác ABC thì $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ với điểm M bất kì.

- Điều kiện cần và đủ để hai vecto $\vec{a}$ và $\vec{b}$ ( ≠ 0) cùng phương là có một số thực k để $\vec{a} = k \vec{b}$ .

- Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để $\vec{A B} = k \vec{A C}$ .

Nhận xét: Trong mặt phẳng, cho hai vecto $\vec{a}$ và $\vec{b}$ không cùng phương. Với mỗi vecto $\vec{c}$ có duy nhất cặp số (x; y) thoả mãn $\vec{c} = x \vec{a} + y \vec{b}$ .

12. Tích vô hướng của hai vecto

12.1. Tích vô hướng của hai vectơ có cùng điểm đầu

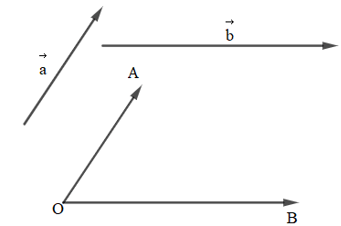
- Góc giữa hai vecto $\vec{O A}$ , $\vec{O B}$ là góc giữa hai tia OA, OB và được kí hiệu là $(\vec{O A}, \vec{O B})$

- Tích vô hướng của hai vecto $\vec{O A}$ và $\vec{O B}$ là một số thực, kí hiệu là $\vec{O A} . \vec{O B}$ , được xác định bởi công thức: $\vec{O A}$ . $\vec{O B}$ =| $\vec{O A}$ |.| $\vec{O B}$ |.cos $(\vec{O A}, \vec{O B})$ .

12.2. Tích vô hướng của hai vectơ tùy ý

Định nghĩa:

Cho hai vecto $\vec{a}$ , $\vec{b}$ khác $\vec{0}$ . Lấy một điểm O và vẽ vecto $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}$ (Hình vẽ).

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

+ Góc giữa hai vecto $\vec{a}$ , $\vec{b}$ , kí hiệu $(\vec{a}, \vec{b})$ , là góc giữa hai vecto $\vec{O A}$ , $\vec{O B}$ .

+ Tích vô hướng của hai vecto $\vec{a}$ và $\vec{b}$ , kí hiệu $\vec{a} . \vec{b}$ là tích vô hướng của hai vecto $\vec{O A}$ và $\vec{O B}$ . Như vậy, tích vô hướng của hai vecto $\vec{a}$ và $\vec{b}$ là một số thực được xác định bởi công thức: $\vec{a} . \vec{b} =$ | $\vec{a}$ |.| $\vec{b}$ |.cos $(\vec{a}, \vec{b})$ .

Quy ước: Tích vô hướng của một vecto bất kì với vecto là số 0.

Chú ý:

+) $(\vec{a}, \vec{b}) = (\vec{b}, \vec{a})$

+) Nếu $(\vec{a}, \vec{b})$ = 90° thì ta nói hai vecto $\vec{a}$ , $\vec{b}$ vuông góc với nhau, kí hiệu $\vec{a}$ ⊥ $\vec{b}$ hoặc $\vec{b}$ ⊥ $\vec{a}$ . Khi đó $\vec{a} . \vec{b} =$ | $\vec{a}$ |.| $\vec{b}$ |.cos $90 ° = 0$ .

+) Tích vô hướng của hai vecto cùng hướng bằng tích hai độ dài của chúng.

+) Tích vô hướng của hai vecto ngược hướng bằng số đối của tích hai độ dài của chúng.

12.3 Tính chất

Với hai vecto bất kì $\vec{a}$ , $\vec{b}$ và số thực k tùy ý, ta có:

+) $\vec{a} . \vec{b} = \vec{b} . \vec{a}$ (tính chất giao hoán);

+) $\vec{a} . (\vec{b} + \vec{c}) = \vec{a} . \vec{b} + \vec{a} . \vec{c}$ (tính chất phân phối);

+) $(k \vec{a}) \vec{b} = k (\vec{a} . \vec{b}) = \vec{a} . (k \vec{b})$ ;

+) ${\vec{a}}^{2}$ ≥ 0, ${\vec{a}}^{2}$ = 0 ⟺ $\vec{a} = \vec{0}$ .

Trong đó, kí hiệu $\vec{a} . \vec{a} = {\vec{a}}^{2}$ và biểu thức này được gọi là bình phương vô hướng của vecto .

Bài tập tổng hợp Toán 10 Chương 4

Bài 1: Không sử dụng máy tính cầm tay, tính giá trị các biểu thức sau:

a) A = 3 – sin²90° + 2cos²60° - 3tan²45°

b) B = a²sin90° + b²cos90° + c²cos180°

Hướng dẫn giải:

a) A = 3 – sin²90° + 2cos²60° - 3tan²45°

= 3 – 1² + 2. ${(\frac{1}{2})}^{2}$ - 3. ${(\frac{\sqrt{2}}{2})}^{2}$

= 1.

b) B = a²sin90° + b²cos90° + c²cos180°

= a².1 + b².0 + c².(-1)

= a² – c².

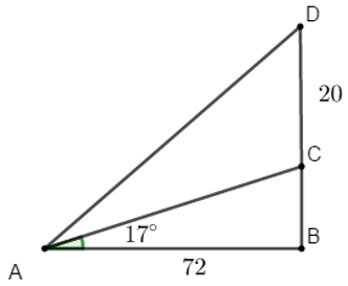
Bài 2:Một cây cột điện cao 20m được đóng trên một triền dốc thẳng nghiêng hợp với phương nằm ngang một góc 17°. Người ta nối một dây cáp từ đỉnh cột điện đến cuối dốc. Tính chiều dài của dây cáp biết rằng đoạn đường từ đáy cọc đến cuối dốc bằng 72 m (làm tròn đến chữ số thập phân thứ 2).

Hướng dẫn giải:

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Bài toán được mô phỏng lại như hình vẽ vớiA, B lần lượt là điểm cuối dốc, chân của triền dốc; C, D lần lượt là chân và đỉnh của cây cột điện.

Suy ra chiều dài của dây cáp là đoạn AD.

Theo bài ra ta có: CD = 20m, AB = 72m, $\hat{C A B}$ = 17°, $\hat{A B D}$ = 90°.

$\hat{A C B}$ = 180° - $\hat{C A B}$ - $\hat{A B D}$ = 180° - 17° - 90° = 73° (tổng ba góc một tam giác bằng 180°).

$\hat{A C D}$ = 180° - $\hat{A C B}$ = 180° - 73° = 107°

Tam giác ABC vuông tại B ⇒ AC = $\frac{A B}{\cos \hat{C A B}} = \frac{72}{\cos 17 °}$ ≈ 75,3 (m)

Áp dụng định lí cosin trong tam giác ACD, ta có:

AD² = AC² + CD² – 2AC.CD. $\cos \hat{A C D}$

= (75,3)² + 20² – 2.75,3.20.cos107° ≈ 6950,7

AD = 83,4m

Vậy chiều dài của dây cáp là 83,4m.

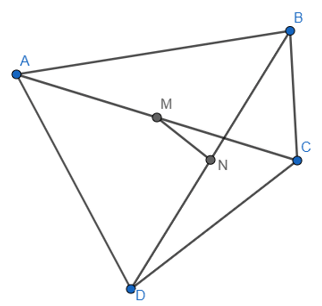
Bài 3: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: $\vec{A B} + \vec{C D} = 2 \vec{M N}$ .

Hướng dẫn giải:

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Ta có:

$\vec{M N} = \vec{M A} + \vec{A B} + \vec{B N}$

$\vec{M N} = \vec{M C} + \vec{C D} + \vec{D N}$

Vì M, N lần lượt là trung điểm của hai đường chéo AC và BD

Suy ra:

$\vec{M A} + \vec{M C} = \vec{0}$

$\vec{B N} + \vec{D N} = \vec{0}$

⇒ $2 \vec{M N} = \vec{M A} + \vec{A B} + \vec{B C} + \vec{M C} + \vec{C D} + \vec{D N}$

$= (\vec{M A} + \vec{M C}) + \vec{A B} + \vec{C D} + (\vec{B N} + \vec{D N})$

= $\vec{0} + \vec{A B} + \vec{C D} + \vec{0}$

= $\vec{A B} + \vec{C D}$ (đpcm).

Bài 4: Cho tam giác ABC vuông cân tại A. Có đường cao AH, G là trọng tâm của tam giác ABC. Tính độ dài vecto $\vec{G A} + \vec{G B} + \vec{G C}$ .

Hướng dẫn giải:

Vì G là trọng tâm tam giác ABC nên ta áp dụng quy tắc trọng tâm có:

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

⇒ | $\vec{G A} + \vec{G B} + \vec{G C}$ | = | $\vec{0}$ | = 0

Vậy độ dài vecto $\vec{G A} + \vec{G B} + \vec{G C}$ là 0.

Bài 5: Cho tứ giác ABCD. Gọi M, N lần lượt thuộc các đoạn thẳng AB, CD sao cho MB = 2MA và NC = 2ND. Chứng minh rằng: $\vec{M N} = \frac{2}{3} \vec{A D} + \frac{1}{3} \vec{B C}$ .

Hướng dẫn giải:

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Áp dụng quy tắc cộng vecto, ta có:

$\vec{M N} = \vec{M A} + \vec{A D} + \vec{D N}$ (1)

$\vec{M N} = \vec{M B} + \vec{B C} + \vec{C N}$ (2)

Nhân hai vế của phương trình (1) với 2 ta có:

$2 \vec{M N} = 2 \vec{M A} + 2 \vec{A D} + 2 \vec{D N}$ (3)

Cộng hai vế của (2) và (3) ta có:

$3 \vec{M N} = \vec{M B} + \vec{B C} + \vec{C N} + 2 \vec{M A} + 2 \vec{A D} + 2 \vec{D N}$

⟺ $3 \vec{M N} = (2 \vec{M A} + \vec{M B}) + 2 \vec{A D} + \vec{B C} + (2 \vec{D N} + \vec{C N})$

Vì M, N lần lượt thuộc các đoạn thẳng AB, CD (M, N lần lượt nằm giữa đoạn thẳng AB và CD).

⇒ $\vec{M A}, \vec{M B}$ và $\vec{D N}, \vec{C N}$ là hai cặp vecto ngược hướng.

Mà MB = 2MA và NC = 2ND nên ta có:

$2 \vec{M A} + \vec{M B} = \vec{0}$

$2 \vec{D N} + \vec{C N} = \vec{0}$

Suy ra:

$3 \vec{M N} = 2 \vec{A D} + \vec{B C}$

⇒ $\vec{M N} = \frac{2}{3} \vec{A D} + \frac{1}{3} \vec{B C}$ (đpcm).

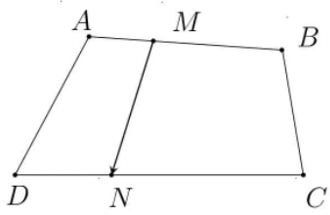
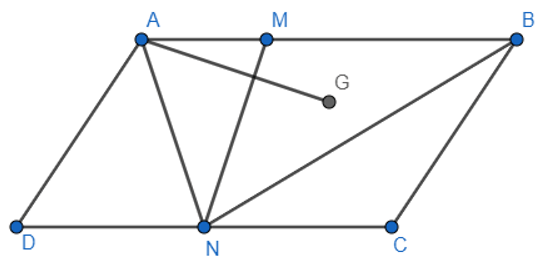
Bài 6: Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vecto $\vec{A N}, \vec{M N}, \vec{A G}$ qua các vecto $\vec{A B}$ và $\vec{A C}$ .

Hướng dẫn giải:

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

+ Vì ABCD là hình bình hành nên $\vec{B A} = \vec{C D}$

Ta lại có: CD = 2CN nên N là trung điểm của CD.

Mà $\vec{C D}$ và $\vec{C N}$ là hai vecto cùng hướng.

⇒ $\vec{C D} = 2 \vec{C N}$ .

⇔ $\vec{C N} = \frac{1}{2} \vec{C D} \Leftrightarrow \vec{C N} = \frac{1}{2} \vec{B A} \Leftrightarrow \vec{C N} = - \frac{1}{2} \vec{A B}$

Suy ra :

$\vec{A N} = \vec{A C} + \vec{C N} = \vec{A C} - \frac{1}{2} \vec{A B}$

+ Ta có: AB = 3AM ⇒ AM = $\frac{1}{3}$ AB

Mà $\vec{A M}$ và $\vec{A B}$ là hai vecto cùng hướng.

⇒ $\vec{A M} = \frac{1}{3} \vec{A B}$

⇒ $\vec{M A} = - \frac{1}{3} \vec{A B}$

⇒ $\vec{M N} = \vec{M A} + \vec{A N} = - \frac{1}{3} \vec{A B} + (\vec{A C} - \frac{1}{2} \vec{A B}) = - \frac{5}{6} \vec{A B} + \vec{A C}$

Vì G là trọng tâm tam giác MNB nên:

$3 \vec{A G} = \vec{A M} + \vec{A N} + \vec{A B} = \frac{1}{3} \vec{A B} + \vec{A C} - \frac{1}{2} \vec{A B} + \vec{A B} = \frac{5}{6} \vec{A B} + \vec{A C}$

⇒ $\vec{A G} = \frac{5}{18} \vec{A B} + \frac{1}{3} \vec{A C}$

Vậy:

$\vec{A N} = \vec{A C} - \frac{1}{2} \vec{A B}$

$\vec{M N} = - \frac{5}{6} \vec{A B} + \vec{A C}$

$\vec{A G} = \frac{5}{18} \vec{A B} + \frac{1}{3} \vec{A C}$

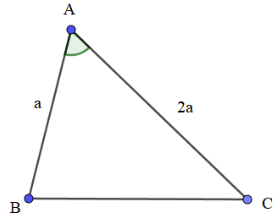
Bài 7: Cho tam giác ABC, biết AB = a, AC = 2a, $\hat{A}$ = 60°. Sử dụng các kiến thức về vecto, tính độ dài cạnh BC.

Hướng dẫn giải:

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều

Áp dụng quy tắc hiệu hai vecto ta có:

$\vec{B C} = \vec{A C} - \vec{A B}$

⟹ ${\vec{B C}}^{2} = {(\vec{A C} - \vec{A B})}^{2} = {\vec{A C}}^{2} - 2 \vec{A C} . \vec{A B} + {\vec{A B}}^{2}$

Ta có:

${\vec{A C}}^{2} = | \vec{A C} |^{2}$ = AC² = (2a)² = 4a²

${\vec{A B}}^{2} = | \vec{A B} |^{2}$ = AB² = a²

$\vec{A C} . \vec{A B}$ = | $\vec{A C}$ |.| $\vec{A B}$ |.cos $(\vec{A C}, \vec{A B})$ = AC.AB.cos $\hat{B A C}$

= 2a.a.cos60° = 2.a.a. $\frac{1}{2}$ = a²

⟹ ${\vec{B C}}^{2}$ = 4a² – 2a² + a² = 3a²

⟹ BC² = $| \vec{B C} |^{2}$ = ${\vec{B C}}^{2}$ = 3a²

⟹ BC = $\sqrt{3 a^{2}}$ = $a \sqrt{3}$ .

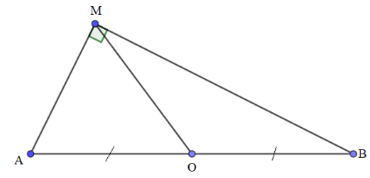
Bài 8: Cho đoạn thẳng AB có trung điểm O, điểm M tùy ý khác O, A, B và không thuộc AB, biết 4OM² = AB². Sử dụng các kiến thức về vecto, chứng minh MA ⊥ MB.

Hướng dẫn giải:

Tổng hợp lý thuyết Toán 10 Chương 4 Cánh diều