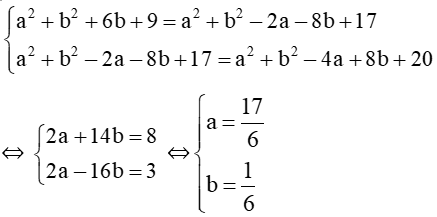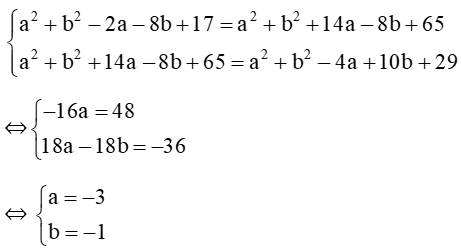Phương trình đường tròn (Lý thuyết Toán lớp 10) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 5: Phương trình đường tròn sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Phương trình đường tròn (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Phương trình đường tròn

I. Phương trình đường tròn

1. Phương trình đường tròn

Nhận xét: Với hai điểm I(a; b) và M(x; y) trong mặt phẳng tọa độ Oxy, ta có:

IM = $\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}$.

* Phương trình chính tắc của đường tròn:

Phương trình đường tròn tâm I(a ; b) bán kính R là (x – a)² + (y – b)² = R².

* Phương trình tổng quát của đường tròn

– Ta có thể viết phương trình (x – a)² + (y – b)² = R² của đường tròn tâm I(a ; b) bán kính R về phương trình có dạng x² + y² – 2ax – 2by + c = 0. Dạng đó thường được gọi là phương trình tổng quát của đường tròn.

– Phương trình có dạng x² + y² – 2ax – 2by + c = 0 là phương trình đường tròn khi và chỉ khi a² + b² > c. Lúc này đường tròn có tâm I(a ; b) bán kính R = $\sqrt{a^2+b^2-c}$.

Ví dụ:

a) Viết phương trình chính tắc của đường tròn tâm I(1 ; 2) và bán kính R= 3;

b) Phương trình x² + y² – 6x + 4y + 5 = 0 có phải là phương trình tổng quát của đường tròn không? Nếu có, hãy tìm tâm và bán kính của đường tròn đó.

Hướng dẫn giải

a) Phương trình chính tắc của đường tròn tâm I(1 ; 2) và bán kính R= 3 là (x – 1)² + (y – 2)² = 3² ⇔ (x – 1)² + (y – 2)² = 9

Vậy phương trình chính tắc của đường tròn tâm I(1 ; 2) và bán kính R= 3 là (x – 1)² + (y – 2)² = 9.

b) Phương trình x² + y² – 6x + 4y + 5 = 0 có dạng x² + y² – 2ax – 2by + c = 0 với a = 3, b = –2, c = 5.

Ta có a² + b² = 3² + (–2)² = 13 > 5 nên a² + b² > c.

Do đó, phương trình x² + y² – 6x + 4y + 5 = 0 là phương trình tổng quát của một đường tròn tâm là I(3 ; –2) và bán kính R = $\sqrt{a^2+b^2-c}$ = $\sqrt{3^2+{\left(-2\right)}^2-5}$ = $\sqrt{8}$.

Vậy phương trình x² + y² – 6x + 4y + 5 = 0 là phương trình tổng quát của một đường tròn tâm là I(3 ; –2) và bán kính R = $\sqrt{8}$.

2. Phương trình đường tròn đi qua ba điểm không thẳng hàng

Có duy nhất một đường tròn đi qua ba điểm không thẳng hàng cho trước nên ta có thể lập được phương trình đường tròn đó khi biết tọa độ của ba điểm nói trên .

Ví dụ: Lập phương trình đường tròn đi qua ba điểm A(0 ; –3), B(1 ; 4), C(2 ; –4).

Hướng dẫn giải

Giả sử tâm của đường tròn là I(a ; b).

Ta có IA = IB = IC ⇔ IA² = IB² = IC².

IA = $\sqrt{{\left(0-a\right)}^2+{\left(-3-b\right)}^2}$ ⇒ IA² = (0 – a)² + (–3 – b)² = a² + b² + 6b + 9.

IB = $\sqrt{{\left(1-a\right)}^2+{\left(4-b\right)}^2}$ ⇒ IB² = (1 – a)² + (4 – b)² = a² + b² – 2a – 8b + 17.

IC = $\sqrt{{\left(2-a\right)}^2+{\left(-4-b\right)}^2}$ ⇒ IC² = (2 – a)² + (–4 – b)² = a² + b² – 4a + 8b + 20.

Vì IA² = IB², IB² = IC² nên:

Suy ra tâm I của đường tròn có tọa độ là $\left(\frac{17}{6};\frac{1}{6}\right)$, bán kính đường tròn

R = IA = $\sqrt{{\left(0-a\right)}^2+{\left(-3-b\right)}^2}$ = $\sqrt{{\left(0-\frac{17}{6}\right)}^2+{\left(-3-\frac{1}{6}\right)}^2}$= $\frac{5\sqrt{26}}{6}$.

Khi đó phương trình đường tròn là ${\left(x-\frac{17}{6}\right)}^2+{\left(y-\frac{1}{6}\right)}^2=\frac{650}{36}$.

Vậy phương trình đường tròn là ${\left(x-\frac{17}{6}\right)}^2+{\left(y-\frac{1}{6}\right)}^2=\frac{650}{36}$.

II. Phương trình tiếp tuyến của đường tròn

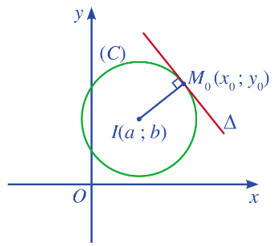
Cho đường tròn (C) tâm I(a ; b) và điểm M₀(x₀ ; y₀) nằm trên đường tròn đó. Gọi ∆ là tiếp tuyến của đường tròn (C) tại điểm M₀(x₀ ; y₀). Khi đó, ta có:

– Đường thẳng ∆ đi qua điểm M₀(x₀ ; y₀) và có vec tơ pháp tuyến $\overrightarrow{I{M}_0}$ = (x₀ – a ; y₀ – b).

– Phương trình tiếp tuyến ∆ là (x₀ – a)(x – x₀) + (y₀ – b)(y – y₀) = 0.

Ví dụ: Lập phương trình tiếp tuyến của đường tròn (C) : x² + y² – 2x + 4y – 20 = 0 tại điểm M(4; 2).

Hướng dẫn giải

Phương trình của đường tròn (C) : x² + y² – 2x + 4y – 20 = 0 có dạng x² + y² – 2ax – 2by + c = 0, với a = 1, b = –2.

Do đó tâm của đường tròn (C) là I(1 ; –2).

Phương trình tiếp tuyến của (C) tại M(4; 2) có dạng:

(4 – 1)(x – 4) + (2 + 2)(y – 2) = 0 ⇔ 3x + 4y – 20 = 0.

Vậy phương trình tiếp tuyến của (C) tại M(4; 2) là 3x + 4y – 20 = 0.

Bài tập Phương trình đường tròn

Bài 1: Phương trình nào sau đây là phương trình đường tròn. Hãy tìm tâm và bán kính của đường tròn đó.

a) x² + y² – x – 7y = 0;

b) x² + y² – 6x + 8y + 100 = 0;

Hướng dẫn giải

a) Phương trình x² + y² – x – 7y = 0 có dạng x² + y² – 2ax – 2by + c = 0, với a = $\frac{1}{2}$, b = $\frac{7}{2}$, c = 0.

Ta có a² + b² = ${\left(\frac{1}{2}\right)}^2+{\left(\frac{7}{2}\right)}^2$ = 12,5 > 0 nên a² + b² > c.

Do đó, phương trình x² + y² – x – 7y = 0 là phương trình tổng quát của một đường tròn tâm là $I\left(\frac{1}{2};\frac{7}{2}\right)$ và bán kính R = $\sqrt{a^2+b^2-c}$ = $\sqrt{{\left(\frac{1}{2}\right)}^2+{\left(\frac{7}{2}\right)}^2-0}$ = $\sqrt{12,5}$.

Vậy phương trình x² + y² – x – 7y = 0 là phương trình tổng quát của một đường tròn tâm là $I\left(\frac{1}{2};\frac{7}{2}\right)$ và bán kính R = $\sqrt{12,5}$.

b) Phương trình x² + y² – 6x + 8y + 100 = 0 có dạng x² + y² – 2ax – 2by + c = 0, với a = 3, b = –4, c = 100.

Ta có a² + b² = 3² + (–4)² = 25 < 100 nên a² + b² < c.

Do đó, phương trình x² + y² – 6x + 8y + 100 = 0 không là phương trình tổng quát của đường tròn.

Vậy phương trình x² + y² – 6x + 8y + 100 = 0 không là phương trình tổng quát của đường tròn.

Bài 2: Lập phương trình đường tròn trong mỗi trường hợp sau:

a) Đường tròn tâm I(–2 ; 3) và bán kính bằng 1.

b) Đường tròn tâm I(0 ; –3) và đi qua điểm A(4; 8).

c) Đường tròn đi qua ba điểm A(1 ; 4) , B(–7 ; 4), C(2 ; –5).

Hướng dẫn giải

a) Phương trình đường tròn tâm I(–2 ; 3) và bán kính bằng 1 có dạng (x + 2)² + (y – 3)² = 1².

Vậy đường tròn tâm I(–2 ; 3) và bán kính bằng 1 có phương trình là (x + 2)² + (y – 3)² = 1.

b) Đường tròn tâm I(0 ; –3) và đi qua điểm A(4; 8) nên bán kính đường tròn này là R = IA = $\sqrt{{\left(4-0\right)}^2+{\left(8+3\right)}^2}$ = $\sqrt{137}$.

Do đó phương trình đường tròn tâm I(0 ; –3) bán kính R = $\sqrt{137}$ là: (x – 0)² + (y + 3)² = 137 ⇔ x² + (y + 3)² = 137.

Vậy phương trình đường tròn tâm I(0 ; –3) và đi qua điểm A(4; 8) là x² + (y + 3)² = 137.

c) Giả sử tâm của đường tròn là I(a ; b). A(1 ; 4) , B(–7 ; 4), C(2 ; –5).

Ta có IA = IB = IC ⇔ IA² = IB² = IC².

IA = $\sqrt{{\left(1-a\right)}^2+{\left(4-b\right)}^2}$ ⇒ IA² = (1 – a)² + (4 – b)² = a² + b² –2a – 8b + 17.

IB = $\sqrt{{\left(-7-a\right)}^2+{\left(4-b\right)}^2}$ ⇒ IB² = (–7 – a)² + (4 – b)² = a² + b² + 14a – 8b + 65.

IC = $\sqrt{{\left(2-a\right)}^2+{\left(-5-b\right)}^2}$ ⇒ IC² = (2 – a)² + (–5 – b)² = a² + b² – 4a + 10b + 29.

Vì IA² = IB², IB² = IC² nên:

Suy ra tâm I của đường tròn có tọa độ là (–3 ; –1), bán kính đường tròn

R = IA = $\sqrt{{\left(1-a\right)}^2+{\left(4-b\right)}^2}$ = $\sqrt{{\left(1+3\right)}^2+{\left(4+1\right)}^2}$ = $\sqrt{41}$.

Khi đó phương trình đường tròn là (x + 3)² + (y + 1)² = 41.

Vậy phương trình đường tròn đi qua ba điểm A(1 ; 4) , B(–7 ; 4), C(2 ; –5) là (x + 3)² + (y + 1)² = 41.

Bài 3: Lập phương trình tiếp tuyến của đường tròn (C): (x – 2)² + (y – 1)² = 5 tại điểm C(2 ; $\sqrt{5}$ + 1).

Hướng dẫn giải

Đường tròn (C) có tâm I(2 ; 1) và bán kính R = $\sqrt{5}$.

Phương trình tiếp tuyến của (C) tại C(2 ; $\sqrt{5}$ + 1) có dạng:

(2 – 2)(x – 2) + ($\sqrt{5}$ + 1 – 1)(y – $\sqrt{5}$ – 1) = 0 ⇔ $\sqrt{5}$y – 5$\sqrt{5}$ – $\sqrt{5}$ = 0.

Vậy phương trình tiếp tuyến của (C) tại C(2 ; $\sqrt{5}$ + 1) là $\sqrt{5}$y – 5$\sqrt{5}$ – $\sqrt{5}$ = 0.

Học tốt Phương trình đường tròn

Các bài học để học tốt Phương trình đường tròn Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài 5: Phương trình đường tròn