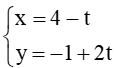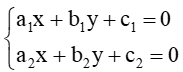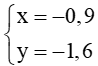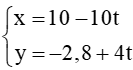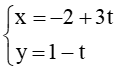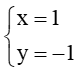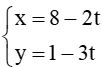Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Lý thuyết Toán lớp 10) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

I. Vị trí tương đối của hai đường thẳng

Trong mặt phẳng tọa độ, cho hai đường thẳng ∆₁ và ∆₂ lần lượt có vectơ chỉ phương là $\overrightarrow{u_1}$, $\overrightarrow{u_2}$. Khi đó

a) ∆₁ cắt ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ không cùng phương.

b) ∆₁ song song với ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.

c) ∆₁ trùng với ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ cùng phương và có một điểm thuộc cả hai đường thẳng đó.

Chú ý:

+ ∆₁ vuông góc với ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ vuông góc với nhau.

+ Khi xét vị trí tương đối của hai đường thẳng, có thể dựa vào cặp vec tơ pháp tuyến của hai đường thẳng đó.

Ví dụ: Xét vị trí tương đối của mỗi cặp đường thẳng sau:

a) ∆₁: 3x + 6y – 7 = 0 và ∆₂: x + 2y + 5 = 0;

b) ∆₃: –3x – 2y + 4 = 0 và ∆₄:

Hướng dẫn giải

a) Đường thẳng ∆₁ có vectơ pháp tuyến $\overrightarrow{n_1}$ = (3 ; 6). Đường thẳng ∆₂ có vectơ pháp tuyến $\overrightarrow{n_2}$ = (1; 2).

Ta thấy $\overrightarrow{n_1}$ = 3$\overrightarrow{n_2}$ nên $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ cùng phương.

Suy ra ∆₁ và ∆₂ song song hoặc trùng nhau.

Lấy điểm A(–5 ; 0) thuộc ∆₂. Thay tọa độ của điểm A vào phương trình của ∆₁ ta có:

3.(–5) + 6.0 – 7 = 0 ⇔ –22 = 0 (vô lý)

Suy ra A ∉∆₁.

Suy ra ∆₁ và ∆₂ song song.

Vậy ∆₁ và ∆₂ song song.

b) Đường thẳng ∆₃ có vectơ pháp tuyến $\overrightarrow{n_3}$ = (–3 ; –2) nên có vectơ chỉ phương là $\overrightarrow{u_3}$ = (2 ; –3).

Đường thẳng ∆₄ có vec tơ chỉ phương $\overrightarrow{u_4}$ = (–1 ; 2).

Ta thấy $\frac{2}{-1}\ne \frac{-3}{2}$ nên $\overrightarrow{u_3}$ và $\overrightarrow{u_4}$ không cùng phương.

Suy ra ∆₃ và ∆₄ cắt nhau.

Vậy ∆₃ và ∆₄ cắt nhau.

Nhận xét: Cho hai đường thẳng ∆₁ và ∆₂ có phương trình lần lượt là:

a₁x + b₁y + c₁ = 0 và a₂x + b₂y + c₂ = 0.

Xét hệ (I)

a) ∆₁ cắt ∆₂ khi và chỉ khi hệ (I) có nghiệm duy nhất.

b) ∆₁ song song với ∆₂ khi và chỉ khi hệ (I) vô nghiệm.

c) ∆₁ trùng với ∆₂ khi và chỉ khi hệ (I) có vô số nghiệm.

Ví dụ: Xét vị trí tương đối của các cặp đường thẳng sau:

d₁: –4x + y – 2 = 0 và d₂: 2x + 2y + 5 = 0;

Hướng dẫn giải

Tọa độ giao điểm của đường thẳng d₁ và đường thẳng d₂ là nghiệm của hệ phương trình

Hệ 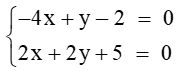có nghiệm duy nhất là

Suy ra d₁ và d₂ cắt nhau tại điểm có tọa độ (–0,9 ; –1,6).

Vậy d₁ và d₂ cắt nhau tại điểm có tọa độ (–0,9 ; –1,6).

II. Góc giữa hai đường thẳng

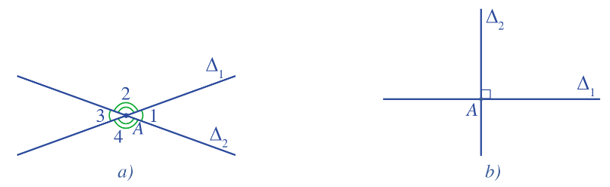
– Hai đường thẳng ∆₁ và ∆₂ cắt nhau tạo thành bốn góc.

+ Nếu hai đường thẳng ∆₁ và ∆₂ không vuông góc với nhau thì góc nhọn trong bốn góc tạo thành được gọi là góc giữa hai đường thẳng ∆₁ và ∆₂.

+ Nếu hai đường thẳng ∆₁ và ∆₂ vuông góc với nhau thì ta nói góc giữa hai đường thẳng ∆₁ và ∆₂ bằng 90^o.

- Góc giữa hai đường thẳng ∆₁ và ∆₂ được kí hiệu $\left(\widehat{{∆}_1,{∆}_2}\right)$ và (∆₁, ∆₂).

Quy ước: Khi ∆₁ song song hoặc trùng với ∆₂, ta nói góc giữa hai đường thẳng ∆₁ và ∆₂ bằng 0°.

Nhận xét: Góc giữa hai đường thẳng luôn bé hơn hoặc bằng 90°, tức là (∆₁, ∆₂) ≤ 90°.

– Trong mặt phẳng tọa độ, cho hai đường thẳng ∆₁ và ∆₂ có vectơ chỉ phương lần lượt là $\overrightarrow{u_1}$ = (a₁; b₁) , $\overrightarrow{u_2}$ = (a₂; b₂) . Ta có:

cos(∆₁, ∆₂) = $\frac{|\overrightarrow{u_1}.\overrightarrow{u_2}|}{\left|\overrightarrow{u_1}\right|.\left|\overrightarrow{u_2}\right|}=\frac{|a_1{a}_2+b_1{b}_2|}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}$.

Nhận xét:

+ ∆₁⊥∆₂⇔ a₁a₂ + b₁b₂ = 0.

+ Cho hai đường thẳng ∆₁và∆₂ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}$, $\overrightarrow{n_2}$. Ta cũng có:

cos(∆₁, ∆₂) = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{|\overrightarrow{n_1}.\overrightarrow{n_2}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}$.

Ví dụ: Tính số đo góc giữa hai đường thẳng ∆₁và∆₂ trong mỗi trường hợp sau:

a) ∆₁: x + 2y – 5 = 0 và ∆₂: 2x + 3y – 4 = 0;

b) ∆₃: 3x – 2y + 1 = 0 và ∆₄: .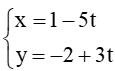

Hướng dẫn giải

a) Đường thẳng ∆₁: x + 2y – 5 = 0 có vectơ pháp tuyến là $\overrightarrow{n_1}$ = (1 ; 2); Đường thẳng ∆₂: 2x + 3y – 4 = 0 có vec tơ pháp tuyến là $\overrightarrow{n_2}$ = (2 ; 3).

Do đó:

cos(∆₁, ∆₂) = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{|\overrightarrow{n_1}.\overrightarrow{n_2}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{|1.2+2.3|}{\sqrt{1^2+2^2}.\sqrt{2^2+3^2}}=\frac{8}{\sqrt{65}}$

⇒ (∆₁, ∆₂) ≈ 7°8’.

Vậy góc giữa hai đường thẳng ∆₁và∆₂ khoảng 7°8’.

b) Đường thẳng ∆₃: 3x – 2y + 1 = 0 có vectơ pháp tuyến là $\overrightarrow{n_3}$ = (3 ; –2) nên có vectơ chỉ phương là $\overrightarrow{u_3}$ = (2 ; 3); Đường thẳng ∆₄ có vec tơ chỉ phương là $\overrightarrow{u_4}$ = (–5 ; 3).

Do đó cos(∆₃, ∆₄) = $\frac{|2.\left(-5\right)+3.3|}{\sqrt{2^2+3^2}.\sqrt{{\left(-5\right)}^2+3^2}}=\frac{1}{\sqrt{442}}$.

⇒ (∆₃, ∆₄) ≈ 87°16’.

III. Khoảng cách từ một điểm đến một đường thẳng

Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ có phương trình ax + by + c = 0 (a² + b² > 0) và điểm M(x₀ ; y₀). Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức sau:

d(M, ∆) = $\frac{|a{x}_0+b{y}_0+c|}{\sqrt{a^2+b^2}}$.

Chú ý: Nếu M ∈ ∆ thì d(M, ∆) = 0.

Ví dụ: Tìm khoảng cách từ điểm M(3; 4) đến đường thẳng ∆: 2x + 6y – 3 = 0.

Hướng dẫn giải

Khoảng cách từ M đến đường thẳng ∆ là d(M, ∆) = $\frac{|2.3+6.4-3|}{\sqrt{2^2+6^2}}=\frac{27}{\sqrt{40}}$.

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là $\frac{27}{\sqrt{40}}$.

Bài tập Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 1: Xét vị trí tương đối của các cặp đường thẳng sau:

a) ∆₁: x – y – 2 = 0 và ∆₂: x + 2y + 1 = 0;

b) ∆₃: –2x – 5y + 6 = 0 và ∆₄:

c) ∆₅: 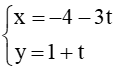và ∆₆:

Hướng dẫn giải

a) Tọa độ giao điểm của đường thẳng ∆₁ và đường thẳng ∆₂ là nghiệm của hệ phương trình

Hệ 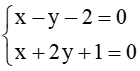có nghiệm duy nhất là

Suy ra ∆₁ và ∆₂ cắt nhau tại điểm có tọa độ (1 ; –1).

Vậy ∆₁ và ∆₂ cắt nhau tại điểm có tọa độ (1 ; –1).

b) Đường thẳng ∆₃: –2x – 5y + 6 = 0 có vectơ pháp tuyến là $\overrightarrow{n_3}$ = (–2 ; –5) nên có vectơ chỉ phương là $\overrightarrow{u_3}$ = (5 ; –2).

Đường thẳng ∆₄ có vectơ chỉ phương là $\overrightarrow{u_4}$ = (–10; 4).

Ta thấy $\overrightarrow{u_4}$ = –2$\overrightarrow{u_3}$ nên $\overrightarrow{u_4}$ và $\overrightarrow{u_3}$ cùng phương.

Khi đó ∆₃ và ∆₄ song song hoặc trùng nhau.

Lấy điểm A(3; 0) thuộc ∆₃, thay tọa độ của A vào phương trình của ∆₄ ta được:

(thỏa mãn).

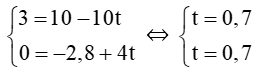
Suy ra A ∈∆₄

Suy ra ∆₃ và ∆₄ trùng nhau.

Vậy ∆₃ và ∆₄ trùng nhau.

c) Đường thẳng ∆₅ có vectơ chỉ phương là $\overrightarrow{u_5}$= (–3 ; 1); đường thẳng ∆₆ có vectơ chỉ phương là $\overrightarrow{u_6}$ = (3 ; –1).

Ta thấy $\overrightarrow{u_5}$ = –1$\overrightarrow{u_6}$ nên $\overrightarrow{u_5}$ và $\overrightarrow{u_6}$ cùng phương

Suy ra ∆₅ và ∆₆ song song hoặc trùng nhau.

Lấy điểm B(–4 ; 1) ∈∆₅. Thay tọa độ của B vào phương trình của ∆₆ ta được:

(vô lý).

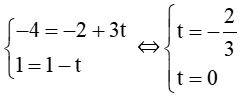
⇒ B ∉∆₆.

Suy ra ∆₅ và ∆₆ song song.

Vậy ∆₅ và ∆₆ song song.

Bài 2: Tìm góc giữa các cặp đường thẳng sau:

a) ∆₁ : x + y – 10 = 0 và ∆₂ : 2x + 99 = 0.

b) d₁: 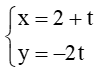và d₂: x – 2y + 3 = 0.

Hướng dẫn giải

a) ∆₁ : x + y – 10 = 0 có vectơ pháp tuyến là $\overrightarrow{n_1}$ = (1 ; 1); Đường thẳng ∆₂ : 2x + 99 = 0 có vectơ pháp tuyến là $\overrightarrow{n_2}$ = (2 ; 0);

cos(∆₁, ∆₂) = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{|\overrightarrow{n_1}.\overrightarrow{n_2}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{|1.2+1.0|}{\sqrt{1^2+1^2}.\sqrt{2^2+0^2}}=\frac{1}{\sqrt{2}}$.

⇒ (∆₁, ∆₂) = 45°.

Vậy góc giữa ∆₁ và ∆₂ bằng 45°.

b) Đường thẳng d₁: 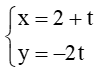có vectơ chỉ phương là $\overrightarrow{u_1}$ = (1 ; –2); đường thẳng d₂: x – 2y + 3 = 0 có vectơ pháp tuyến là $\overrightarrow{n_2}$ = (1; –2) nên có vectơ chỉ phương là $\overrightarrow{u_2}$ = (2; 1).

Khi đó cos(d₁, d₂) = $\frac{|1.2+\left(-2\right).1|}{\sqrt{1^2+{\left(-2\right)}^2}.\sqrt{2^2+1^2}}=\frac{0}{5}=0$.

⇒ (d₁, d₂) = 90°.

Vậy góc giữa d₁ và d₂ bằng 90°.

Bài 3: Tính khoảng cách từ điểm A đến đường thẳng d trong mỗi trường hợp sau:

a) A(3 ; 5) và ∆: 4x + 3y + 1 = 0;

b) A(6 ; –2) và ∆:

Hướng dẫn giải

a) Khoảng cách từ A(3 ; 5) đến đường thẳng ∆ là d(M, ∆) = $\frac{|4.3+3.5+1|}{\sqrt{4^2+3^2}}=\frac{28}{5}$.

Vậy khoảng cách từ điểm A đến đường thẳng ∆ là $\frac{28}{5}$.

b) Thay tọa độ điểm A(6 ; –2) vào phương trình tham số của ∆ ta có:

(thỏa mãn).

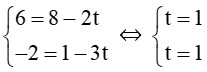
Do đó A ∈ ∆.

Suy ra khoảng cách từ A đến đường thẳng ∆ bằng 0.

Vậy khoảng cách từ A đến đường thẳng ∆ bằng 0.

Học tốt Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Các bài học để học tốt Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng