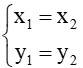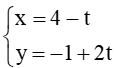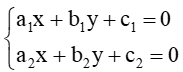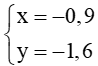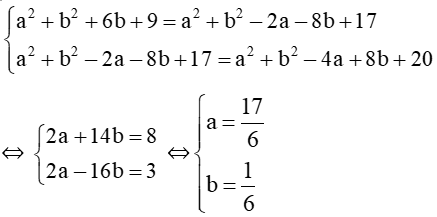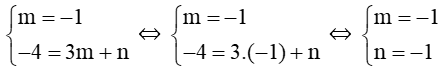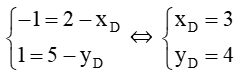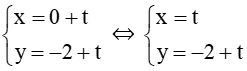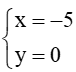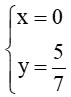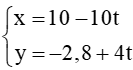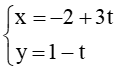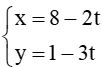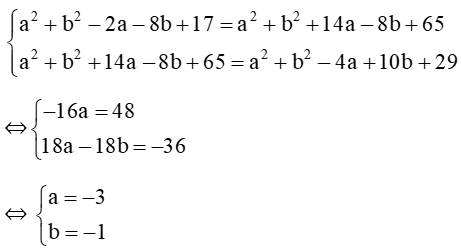Tổng hợp lý thuyết Toán 10 Chương 7 Cánh diều

---

Với Tổng hợp lý thuyết Toán 10 Chương 7: Phương pháp tọa độ trong mặt phẳng sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Tổng hợp lý thuyết Toán 10 Chương 7 Cánh diều

Lý thuyết tổng hợp Toán 10 Chương 7

1. Tọa độ của một điểm

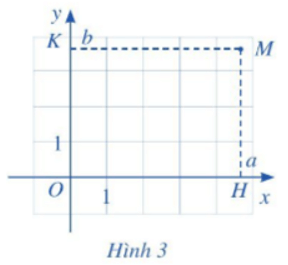
Để xác định tọa độ của một điểm M tùy ý trong mặt phẳng tọa độ Oxy, ta làm như sau (Hình 3):

+ Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

+ Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.

Cặp số (a; b) là tọa độ của điểm M trong mặt phẳng tọa độ Oxy. Ta kí hiệu là M(a ; b).

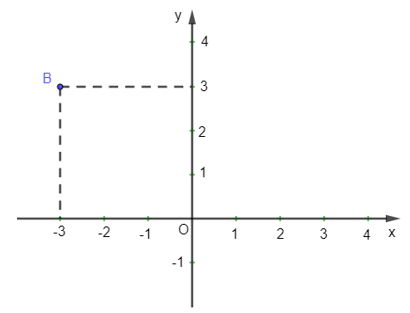
Ví dụ: Xác định tọa độ của điểm B trong hình vẽ sau:

Hướng dẫn giải

+ Từ B kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm ứng với số –3. Số –3 là hoành độ của điểm B.

+ Từ B kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm ứng với số 3. Số 3 là tung độ của điểm M.

Khi đó, cặp số (–3; 3) là tọa độ của điểm B.

Vậy điểm B có tọa độ là B(–3; 3).

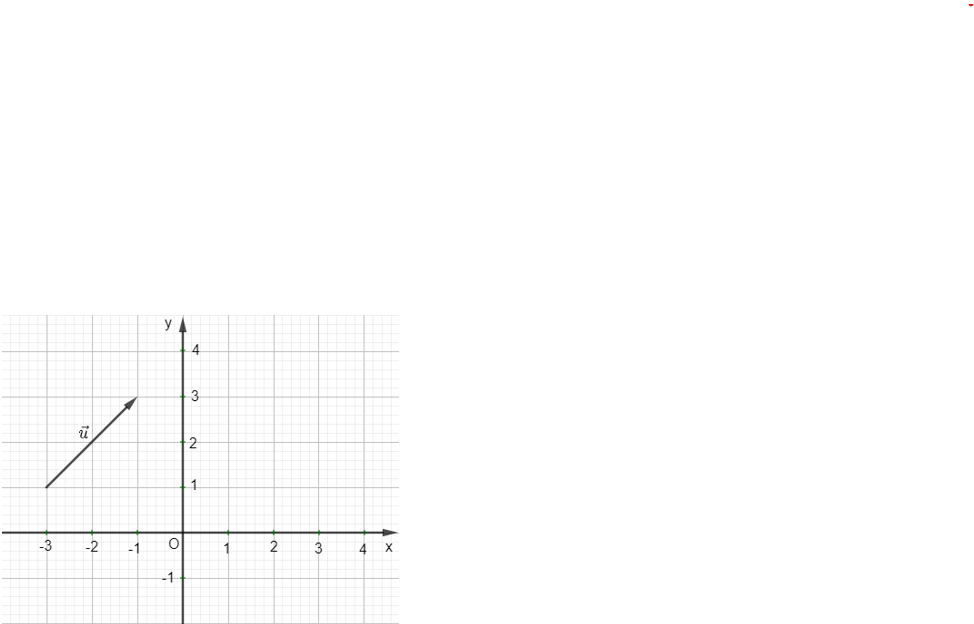
2. Tọa độ của một vectơ

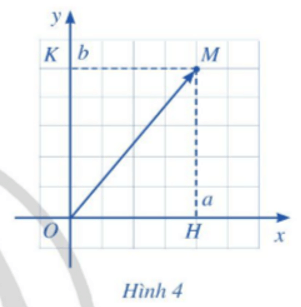
Tọa độ của điểm M được gọi là tọa độ của vectơ $\overrightarrow{OM}$.

Nếu $\overrightarrow{OM}$ có tọa độ (a; b) thì ta viết $\overrightarrow{OM}$ = (a; b) hay $\overrightarrow{OM}$ (a; b), trong đó a gọi là hoành độ của vectơ $\overrightarrow{OM}$ và b gọi là tung độ của vectơ $\overrightarrow{OM}$ (Hình 4).

Chú ý: Trong mặt phẳng tọa độ Oxy, ta có:

+ $\overrightarrow{OM}$ = (a; b) ⇔ M(a ; b).

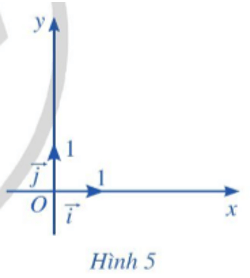
+ Vectơ $\overrightarrow{i}$ có điểm gốc là O và có tọa độ (1; 0) gọi là vectơ đơn vị trên trục Ox.

Vectơ $\overrightarrow{j}$ có điểm gốc là O và có tọa độ (0; 1) gọi là vectơ đơn vị trên trục Oy (Hình 4).

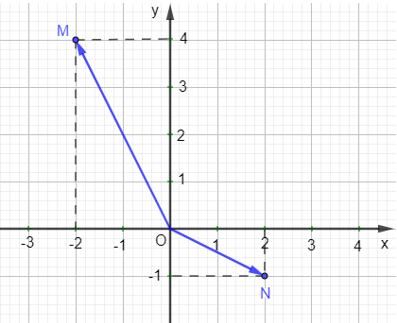
Ví dụ: Tìm tọa độ của vec tơ $\overrightarrow{OM}$, $\overrightarrow{ON}$ trong hình sau:

Hướng dẫn giải

Ta thấy điểm M có tọa độ là (–2 ; 4)

Suy ra $\overrightarrow{OM}$ = (–2 ; 4).

Điểm N có tọa độ là (2 ; –1)

Suy ra $\overrightarrow{ON}$ = (2 ; –1).

Vậy $\overrightarrow{OM}$ = (–2 ; 4) và $\overrightarrow{ON}$ = (2 ; –1).

Nhận xét:

– Với mỗi vectơ $\overrightarrow{u}$, ta xác định được duy nhất một điểm A sao cho $\overrightarrow{OA}$ = $\overrightarrow{u}$.

– Với mỗi vectơ $\overrightarrow{u}$ trong mặt phẳng tọa độ Oxy, tọa độ của vectơ $\overrightarrow{u}$ là tọa độ của điểm A, trong đó A là điểm sao cho $\overrightarrow{OA}$ = $\overrightarrow{u}$.

– Nếu $\overrightarrow{u}$ có tọa độ (a; b) thì ta viết $\overrightarrow{u}$ = (a; b) hay $\overrightarrow{u}$(a; b), trong đó a gọi là hoành độ của vectơ $\overrightarrow{u}$ và b gọi là tung độ của vectơ $\overrightarrow{u}$.

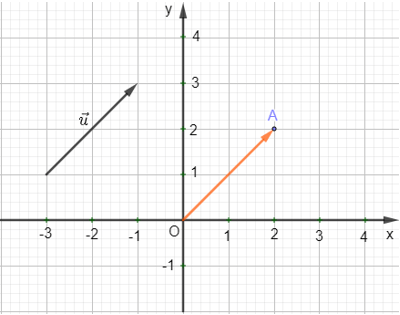
Ví dụ: Tìm tọa độ của vec tơ $\overrightarrow{u}$ trong hình vẽ sau:

Hướng dẫn giải

Ta xác định vec tơ $\overrightarrow{u}$ = $\overrightarrow{OA}$ như hình sau:

Ta thấy điểm A(2 ; 2) nên $\overrightarrow{OA}$ = (2 ; 2).

Suy ra $\overrightarrow{u}$ = (2 ; 2).

Vậy $\overrightarrow{u}$ = (2 ; 2).

Định lí: Trong mặt phẳng tọa độ Oxy, nếu $\overrightarrow{u}$ = (a ; b) thì $\overrightarrow{u}$ = a$\overrightarrow{i}$ + b$\overrightarrow{j}$. Ngược lại, nếu $\overrightarrow{u}$ = a$\overrightarrow{i}$ + b$\overrightarrow{j}$ thì $\overrightarrow{u}$ = (a ; b).

Chú ý: Với $\overrightarrow{a}$ = (x₁ ; y₁) và $\overrightarrow{b}$ = (x₂ ; y₂), ta có $\overrightarrow{a}$ = $\overrightarrow{b}$ ⇔

Như vậy, mỗi vectơ hoàn toàn được xác định khi biết tọa độ của nó.

Ví dụ: Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 3) và vectơ $\overrightarrow{u}$ = (1; – 3).

a) Biểu diễn vectơ $\overrightarrow{u}$ qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

b) Biểu diễn vectơ $\overrightarrow{OM}$ qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

Hướng dẫn giải

a) Vì vectơ $\overrightarrow{u}$ = (1; – 3) nên $\overrightarrow{u}$ = 1$\overrightarrow{i}$ + (– 3)$\overrightarrow{j}$ = $\overrightarrow{i}$ – 3$\overrightarrow{j}$

Vậy $\overrightarrow{u}$ = $\overrightarrow{i}$ – 3$\overrightarrow{j}$.

b) Vì điểm M có tọa độ là (2 ; 3) nên $\overrightarrow{OM}$ = (2 ; 3).

Do đó: $\overrightarrow{OM}$ = 2$\overrightarrow{i}$ + 3$\overrightarrow{j}$.

Vậy $\overrightarrow{OM}$ = 2$\overrightarrow{i}$ + 3$\overrightarrow{j}$.

3. Liên hệ giữa tọa độ của điểm và tọa độ của vec tơ

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(x_A; y_A) và B(x_B; y_B).

Ta có $\overrightarrow{AB}$ = (x_B – x_A ; y_B – y_A).

Ví dụ: Cho hai điểm A(2; –4) và B(1; 5). Hãy tìm tọa độ của vectơ $\overrightarrow{AB}$.

Hướng dẫn giải

Ta có $\overrightarrow{AB}$ = (1 – 2; 5 – (–4)) = (–1 ; 9).

Vậy $\overrightarrow{AB}$ = (–1 ; 9).

4. Biểu thức tọa độ của phép cộng hai vec tơ, phép trừ hai vec tơ, phép nhân một số với một vec tơ

Nếu $\overrightarrow{u}$ = (x₁ ; y₁) và $\overrightarrow{v}$ = (x₂ ; y₂) thì

$\overrightarrow{u}$ + $\overrightarrow{v}$ = ( x₁ + x₂ ; y₁ + y₂);

$\overrightarrow{u}$ – $\overrightarrow{v}$ = ( x₁ – x₂ ; y₁ – y₂);

k$\overrightarrow{u}$ = (kx₁; ky₁) với k ∈ℝ.

Ví dụ: Cho hai vec tơ $\overrightarrow{u}$ = (–5 ; 1) và $\overrightarrow{v}$ = (2 ; –3). Tìm tọa độ của mỗi vec tơ sau:

a) $\overrightarrow{u}$ + $\overrightarrow{v}$;

b) $\overrightarrow{u}$ – $\overrightarrow{v}$;

c) –2$\overrightarrow{v}$.

Hướng dẫn giải

a) Ta có: $\overrightarrow{u}$ + $\overrightarrow{v}$ = (–5 + 2 ; 1 + (–3)) = (–3 ; –2).

Vậy $\overrightarrow{u}$ + $\overrightarrow{v}$ = (–3 ; –2).

b) Ta có $\overrightarrow{u}$ – $\overrightarrow{v}$ = (–5 – 2 ; 1 – (–3)) = (–7 ; 4).

Vậy $\overrightarrow{u}$ – $\overrightarrow{v}$ = (–7 ; 4).

c) Ta có –2$\overrightarrow{v}$ = (–2.2 ; –2.(–3)) = (–4 ; 6).

Vậy –2$\overrightarrow{v}$ = (–4 ; 6).

Nhận xét: Hai vec tơ $\overrightarrow{u}$ = (x₁ ; y₁), $\overrightarrow{v}$ = (x₂ ; y₂) ($\overrightarrow{v}$ ≠ $\overrightarrow{0}$) cùng phương khi và chỉ khi có một số thực k sao cho x₁ = kx₂ và y₁ = ky₂.

Ví dụ: Hai vec tơ $\overrightarrow{u}$ = (–1 ; 2) và $\overrightarrow{v}$ = (4 ; –8) có cùng phương hay không?

Hướng dẫn giải

Ta thấy 4 = –4.(–1) và –8 = –4.2

Do đó hai vectơ $\overrightarrow{u}$ = (–1 ; 2) và $\overrightarrow{v}$ = (4 ; –8) cùng phương với nhau.

Vậy hai vectơ $\overrightarrow{u}$ = (–1 ; 2) và $\overrightarrow{v}$ = (4 ; –8) cùng phương.

5. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác

– Cho hai điểm A(x_A; y_A) và B(x_B; y_B). Nếu M(x_M; y_M) là trung điểm của đoạn thẳng AB thì

$x_M=\frac{x_A+x_B}{2}$ ; $y_M=\frac{y_A+y_B}{2}$.

– Cho tam giác ABC có A(x_A ; y_A), B(x_B ; y_B), C(x_C ; y_C). Nếu G(x_G ; y_G) là trọng tâm của tam giác ABC thì

$x_G=\frac{x_A+x_B+x_C}{3}$; $y_G=\frac{y_A+y_B+y_C}{3}$.

Ví dụ: Cho tam giác ABC có A(0 ; 3), B(–1 ; –4), C(4 ; –2). Hãy tìm tọa độ trung điểm I của cạnh BC và trọng tâm G của tam giác ABC.

Hướng dẫn giải

Gọi tọa độ trung điểm I của cạnh BC và trọng tâm G của tam giác ABC lần lượt là (x_I ; y_I) và (x_G ; y_G).

Khi đó, vì I là trung điểm của BC nên ta có:

$x_I=\frac{x_B+x_C}{2}=\frac{-1+4}{2}=\frac{3}{2}$; $y_I=\frac{y_B+y_C}{2}=\frac{(-4)+(-2)}{2}=-3$.

Suy ra $I\left(\frac{3}{2};-3\right)$.

Vì G là trọng tâm của tam giác ABC nên ta có:

$x_G=\frac{x_A+x_B+x_C}{3}=\frac{0+\left(-1\right)+4}{3}=1$; $y_G=\frac{y_A+y_B+y_C}{3}=\frac{3+\left(-4\right)+\left(-2\right)}{3}=-1$.

Suy ra G(1 ; –1).

Vậy $I\left(\frac{3}{2};-3\right)$ và G(1 ; –1).

6. Biểu thức tọa độ của tích vô hướng

Nếu $\overrightarrow{u}$ = (x₁; y₁) và $\overrightarrow{v}$ = (x₂; y₂) thì $\overrightarrow{u}$.$\overrightarrow{v}$ = x₁x₂ + y₁y₂.

Nhận xét:

a) Nếu $\overrightarrow{a}$ = (x; y) thì |$\overrightarrow{a}$| = $\sqrt{\overrightarrow{a}.\overrightarrow{a}}=\sqrt{x^2+y^2}$.

b) Nếu A(x₁; y₁) và B(x₂; y₂) thì AB = |$\overrightarrow{AB}$| = $\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}$.

c) Với hai vectơ $\overrightarrow{u}$ = (x₁; y₁) và $\overrightarrow{v}$ = (x₂; y₂) đều khác $\overrightarrow{0}$, ta có:

+ $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau khi và chỉ khi x₁x₂ + y₁y₂ = 0.

+ cos($\overrightarrow{u}$, $\overrightarrow{v}$) = $\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\frac{x_1{x}_2+y_1{y}_2}{\sqrt{x_1^2+y_1^2}.\sqrt{x_2^2+y_x^2}}$.

Ví dụ: Cho hai vec tơ $\overrightarrow{u}$ = (3 ; –5) và $\overrightarrow{v}$ = (5 ; 3).

a) Tính |$\overrightarrow{u}$|;

b) Tính $\overrightarrow{u}.\overrightarrow{v}$;

c) Tính góc giữa hai vec tơ $\overrightarrow{u}$ và $\overrightarrow{v}$

Hướng dẫn giải

a) Ta có $\left|\overrightarrow{u}\right|$ = $\sqrt{3^2+{\left(-5\right)}^2}$ = $\sqrt{34}$.

Vậy $\left|\overrightarrow{u}\right|$ = $\sqrt{34}$.

b) Ta có $\overrightarrow{u}.\overrightarrow{v}$ = 3.5 + (–5).3 = 0.

Vậy $\overrightarrow{u}.\overrightarrow{v}$ = 0.

c) Ta có cos($\overrightarrow{u}$, $\overrightarrow{v}$) = $\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}$ = $\frac{3.5+\left(-5\right).3}{\sqrt{3^2+{\left(-5\right)}^2}.\sqrt{5^2+3^2}}=\frac{0}{34}=0$.

Suy ra ($\overrightarrow{u}$, $\overrightarrow{v}$) = 90^o.

Vậy $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau.

7. Phương trình tham số của đường thẳng

a. Vectơ chỉ phương của đường thẳng

Vectơ $\overrightarrow{u}$ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu $\overrightarrow{u}$ ≠ $\overrightarrow{0}$ và giá của $\overrightarrow{u}$ song song hoặc trùng với ∆.

Nhận xét:

– Nếu $\overrightarrow{u}$ là một vectơ chỉ phương của ∆ thì k$\overrightarrow{u}$ (k ≠ 0) cũng là một vectơ chỉ phương của ∆.

– Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ chỉ phương của đường thẳng đó.

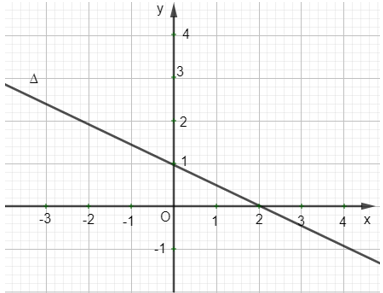
Ví dụ: Đường thẳng ∆ đi qua điểm (2 ; 0) và (0 ; –1) có vectơ chỉ phương $\overrightarrow{u}$ như hình vẽ sau:

b. Phương trình tham số của đường thẳng

Hệ 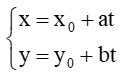(a² + b² > 0 và t là tham số) được gọi là phương trình tham số của đường thẳng ∆ đi qua M₀(x₀ ; y₀₎ và nhận $\overrightarrow{u}$ = (a ; b) làm vectơ chỉ phương.

Nhận xét: Cho đường thẳng ∆ có phương trình tham số là: 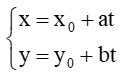(a² + b² > 0 và t là tham số).

+ Với mỗi giá trị cụ thể của t, ta xác định được một điểm trên đường thẳng ∆. Ngược lại, với mỗi điểm trên đường thẳng ∆, ta xác định được một giá trị cụ thể của t.

+ Vectơ $\overrightarrow{u}$ = (a ; b) là một vectơ chỉ phương của ∆.

Ví dụ:

a) Viết phương trình tham số của đường thẳng ∆ đi qua điểm A(1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (–1 ; 3).

b) Cho đường thẳng ∆ có phương trình tham số là 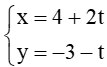. Chỉ ra tọa độ một vectơ chỉ phương của ∆ và một điểm thuộc đường thẳng ∆.

Hướng dẫn giải

a) Phương trình đường thẳng ∆ đi qua điểm A(1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (–1 ; 3) nên có phương trình tham số là .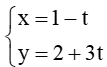

Vậy phương trình tham số của đường thẳng ∆ là .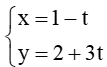

b) Đường thẳng ∆ có phương trình tham số là .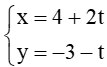

Khi đó ∆ có một vec tơ chỉ phương là (2 ; –1) và điểm (4 ; –3) thuộc ∆.

Vậy ∆ có một vec tơ chỉ phương là (2 ; –1) và điểm (4 ; –3) thuộc ∆.

8. Phương trình tổng quát của đường thẳng

a. Vectơ pháp tuyến của đường thẳng

Vectơ $\overrightarrow{n}$ được gọi là vec tơ pháp tuyến của đường thẳng ∆ nếu $\overrightarrow{n}$ ≠ $\overrightarrow{0}$ và giá của vectơ $\overrightarrow{n}$ vuông góc với ∆.

Nhận xét:

– Nếu $\overrightarrow{n}$ là một vectơ pháp tuyến của ∆ thì k$\overrightarrow{n}$ (k ≠ 0) cũng là một vectơ pháp tuyến của ∆.

– Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của đường thẳng đó.

– Nếu một đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u}$ = (a ; b) thì vectơ $\overrightarrow{n}$ = (–b ; a) là một vectơ pháp tuyến của ∆.

b. Phương trình tổng quát của đường thẳng

Phương trình ax + by + c = 0 (a và b không đồng thời bằng 0) được gọi là phương trình tổng quát của đường thẳng.

Nhận xét:

– Đường thẳng ∆ đi qua điểm M_0­ (x₀ ; y₀) và nhận $\overrightarrow{n}$ = (a ; b) làm vectơ pháp tuyến có phương trình là: a(x – x₀) + b(y – y₀) = 0 ⇔ ax + by + (–ax₀ – by₀) = 0.

– Mỗi phương trình ax + by + c = 0 (a và b không đồng thời bằng 0) đều xác định một đường thẳng ∆ trong mặt phẳng tọa độ nhận một vec tơ pháp tuyến là $\overrightarrow{n}$ = (a ; b).

Ví dụ: Viết phương trình tổng quát của đường thẳng d đi qua điểm A(1; –2) và có vectơ pháp tuyến $\overrightarrow{n}$ = (–2 ; –3).

Hướng dẫn giải

Theo giả thiết, phương trình của đường thẳng d là : –2(x – 1) + (–3).(y + 2) = 0.

Từ đó, ta nhận được phương trình tổng quát của đường thẳng d là –2x – 3y – 4 = 0.

Vậy phương trình tổng quát của d là –2x – 3y – 4 = 0.

c. Những dạng đặc biệt của phương trình tổng quát

Cho đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0).

a) Nếu b = 0 và a ≠ 0 thì phương trình đường thẳng ∆ trở thành ax + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Oy và cắt trục Ox tại điểm $\left(-\frac{c}{a};0\right)$.

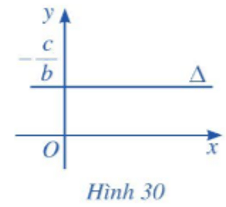
b) Nếu b ≠ 0 và a = 0 thì phương trình đường thẳng ∆ trở thành by + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Ox và cắt trục Oy tại điểm $\left(0;-\frac{c}{b}\right)$ (Hình 30).

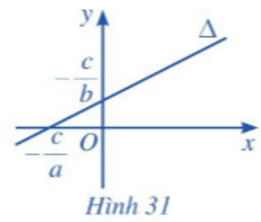
c) Nếu b ≠ 0 và a ≠ 0 thì phương trình đường thẳng ∆ có thể viết thành

y = $-\frac{a}{b}$x – $\frac{c}{b}$.

Khi đó, đường thẳng ∆ là đồ thị hàm số bậc nhất y = $-\frac{a}{b}$x – $\frac{c}{b}$ với hệ số góc là k = $-\frac{a}{b}$ (Hình 31).

Nhận xét:

– Đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0) là đồ thị của hàm số bậc nhất khi và chỉ khi a ≠ 0 và b ≠ 0.

– Phương trình trục hoành là y = 0, phương trình trục tung là x = 0.

Ví dụ:

a) Cho phương trình đường thẳng ∆ là 2x + 4 = 0. Khi đó đường thẳng ∆ song song với trục Oy và cắt trục Ox tại điểm (–2 ; 0)

b) Cho phương trình đường thẳng ∆ là 3x – 9 = 0. Khi đó đường thẳng ∆ song song với trục Ox và cắt trục Oy tại điểm (0 ; 3)

c) Cho phương trình đường thẳng ∆ là x + 2y – 2 = 0. Khi đó, đường thẳng ∆ là đồ thị của hàm số bậc nhất y = $-\frac{1}{2}$x + 1 với hệ số góc k = $-\frac{1}{2}$.

9. Lập phương trình đường thẳng

a. Lập phương trình đường thẳng đi qua một điểm và biết vectơ pháp tuyến

Phương trình đường thẳng ∆ đi qua điểm M₀(x₀ ; y₀) và nhận $\overrightarrow{n}$ = (a ; b) ($\overrightarrow{n}$ ≠ $\overrightarrow{0}$) làm vectơ pháp tuyến là a(x – x₀) + b(y – y₀) = 0.

Ví dụ: Lập phương trình của đường thẳng ∆ đi qua điểm M(2; –2) và có vectơ pháp tuyến $\overrightarrow{n}$ = (2 ; 3).

Hướng dẫn giải

Theo giả thiết, phương trình của đường thẳng ∆ là: 2(x – 2) + 3.(y + 2) = 0.

Từ đó, ta nhận được phương trình của đường thẳng ∆ là 2x + 3y + 2 = 0.

Vậy phương trình của ∆ là 2x + 3y + 2 = 0.

b. Lập phương trình đường thẳng đi qua một điểm và biết vec tơ chỉ phương

Phương trình tham số của đường thẳng ∆ đi qua điểm M₀(x₀ ; y₀) và nhận $\overrightarrow{u}$ = (a ; b) ($\overrightarrow{u}$ ≠ $\overrightarrow{0}$) làm vec tơ chỉ phương là 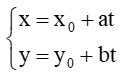(t là tham số).

Nếu a ≠ 0 và b ≠ 0 thì ta còn có thể viết phương trình của đường thẳng ∆ ở dạng: $\frac{x-x_0}{a}=\frac{y-y_0}{b}$.

Ví dụ: Viết phương trình tham số của đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (1 ; –3).

Hướng dẫn giải

Cách 1: Phương trình tham số của đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương $\over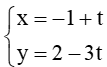rightarrow{u}$ = (1 ; –3) là .

Vậy phương trình tham số của đường thẳng ∆ là .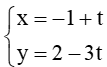

Cách 2: Phương trình đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (1 ; –3) nên có phương trình là $\frac{x+1}{1}=\frac{y-2}{-3}$ ⇔ –3x – y – 1= 0.

Vậy phương trình của đường thẳng ∆ là –3x – y – 1= 0.

c. Lập phương trình đi qua hai điểm

Đường thẳng ∆ đi qua hai điểm A(x₀ ; y₀), B(x₁ ; y₁) nên nhận vectơ $\overrightarrow{AB}$ = (x₁ – x₀ ; y₁ – y₀) làm vectơ chỉ phương. Do đó, phương trình tham số của đường thẳng ∆ là:

(t là tham số).

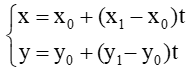
Nếu x₁ – x₀ ≠ 0 và y₁ – y₀ ≠ 0 thì ta còn có thể viết phương trình của đường thẳng ∆ ở dạng: $\frac{x-x_0}{x_1-x_0}=\frac{y-y_0}{y_1-y_0}$.

Ví dụ: Lập phương trình ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3).

Hướng dẫn giải

Phương trình ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3) là

$\frac{x-2}{-1-2}=\frac{y-2}{3-2}$ ⇔ $\frac{x-2}{-3}=\frac{y-2}{1}$ ⇔ x + 3y – 8 = 0.

Vậy phương trình đường thẳng ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3) là x + 3y – 8 = 0.

10. Vị trí tương đối của hai đường thẳng

Trong mặt phẳng tọa độ, cho hai đường thẳng ∆₁ và ∆₂ lần lượt có vectơ chỉ phương là $\overrightarrow{u_1}$, $\overrightarrow{u_2}$. Khi đó

a) ∆₁ cắt ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ không cùng phương.

b) ∆₁ song song với ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.

c) ∆₁ trùng với ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ cùng phương và có một điểm thuộc cả hai đường thẳng đó.

Chú ý:

+ ∆₁ vuông góc với ∆₂ khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ vuông góc với nhau.

+ Khi xét vị trí tương đối của hai đường thẳng, có thể dựa vào cặp vec tơ pháp tuyến của hai đường thẳng đó.

Ví dụ: Xét vị trí tương đối của mỗi cặp đường thẳng sau:

a) ∆₁: 3x + 6y – 7 = 0 và ∆₂: x + 2y + 5 = 0;

b) ∆₃: –3x – 2y + 4 = 0 và ∆₄:

Hướng dẫn giải

a) Đường thẳng ∆₁ có vectơ pháp tuyến $\overrightarrow{n_1}$ = (3 ; 6). Đường thẳng ∆₂ có vectơ pháp tuyến $\overrightarrow{n_2}$ = (1; 2).

Ta thấy $\overrightarrow{n_1}$ = 3$\overrightarrow{n_2}$ nên $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ cùng phương.

Suy ra ∆₁ và ∆₂ song song hoặc trùng nhau.

Lấy điểm A(–5 ; 0) thuộc ∆₂. Thay tọa độ của điểm A vào phương trình của ∆₁ ta có:

3.(–5) + 6.0 – 7 = 0 ⇔ –22 = 0 (vô lý)

Suy ra A ∉∆₁.

Suy ra ∆₁ và ∆₂ song song.

Vậy ∆₁ và ∆₂ song song.

b) Đường thẳng ∆₃ có vectơ pháp tuyến $\overrightarrow{n_3}$ = (–3 ; –2) nên có vectơ chỉ phương là $\overrightarrow{u_3}$ = (2 ; –3).

Đường thẳng ∆₄ có vec tơ chỉ phương $\overrightarrow{u_4}$ = (–1 ; 2).

Ta thấy $\frac{2}{-1}\ne \frac{-3}{2}$ nên $\overrightarrow{u_3}$ và $\overrightarrow{u_4}$ không cùng phương.

Suy ra ∆₃ và ∆₄ cắt nhau.

Vậy ∆₃ và ∆₄ cắt nhau.

Nhận xét: Cho hai đường thẳng ∆₁ và ∆₂ có phương trình lần lượt là:

a₁x + b₁y + c₁ = 0 và a₂x + b₂y + c₂ = 0.

Xét hệ (I)

a) ∆₁ cắt ∆₂ khi và chỉ khi hệ (I) có nghiệm duy nhất.

b) ∆₁ song song với ∆₂ khi và chỉ khi hệ (I) vô nghiệm.

c) ∆₁ trùng với ∆₂ khi và chỉ khi hệ (I) có vô số nghiệm.

Ví dụ: Xét vị trí tương đối của các cặp đường thẳng sau:

d₁: –4x + y – 2 = 0 và d₂: 2x + 2y + 5 = 0;

Hướng dẫn giải

Tọa độ giao điểm của đường thẳng d₁ và đường thẳng d₂ là nghiệm của hệ phương trình

Hệ 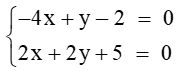có nghiệm duy nhất là

Suy ra d₁ và d₂ cắt nhau tại điểm có tọa độ (–0,9 ; –1,6).

Vậy d₁ và d₂ cắt nhau tại điểm có tọa độ (–0,9 ; –1,6).

11. Góc giữa hai đường thẳng

– Hai đường thẳng ∆₁ và ∆₂ cắt nhau tạo thành bốn góc.

+ Nếu hai đường thẳng ∆₁ và ∆₂ không vuông góc với nhau thì góc nhọn trong bốn góc tạo thành được gọi là góc giữa hai đường thẳng ∆₁ và ∆₂.

+ Nếu hai đường thẳng ∆₁ và ∆₂ vuông góc với nhau thì ta nói góc giữa hai đường thẳng ∆₁ và ∆₂ bằng 90^o.

- Góc giữa hai đường thẳng ∆₁ và ∆₂ được kí hiệu $\left(\widehat{{∆}_1,{∆}_2}\right)$ và (∆₁, ∆₂).

Quy ước: Khi ∆₁ song song hoặc trùng với ∆₂, ta nói góc giữa hai đường thẳng ∆₁ và ∆₂ bằng 0°.

Nhận xét: Góc giữa hai đường thẳng luôn bé hơn hoặc bằng 90°, tức là (∆₁, ∆₂) ≤ 90°.

– Trong mặt phẳng tọa độ, cho hai đường thẳng ∆₁ và ∆₂ có vectơ chỉ phương lần lượt là $\overrightarrow{u_1}$ = (a₁; b₁) , $\overrightarrow{u_2}$ = (a₂; b₂) . Ta có:

cos(∆₁, ∆₂) = $\frac{|\overrightarrow{u_1}.\overrightarrow{u_2}|}{\left|\overrightarrow{u_1}\right|.\left|\overrightarrow{u_2}\right|}=\frac{|a_1{a}_2+b_1{b}_2|}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}$.

Nhận xét:

+ ∆₁⊥∆₂⇔ a₁a₂ + b₁b₂ = 0.

+ Cho hai đường thẳng ∆₁và∆₂ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}$, $\overrightarrow{n_2}$. Ta cũng có:

cos(∆₁, ∆₂) = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{|\overrightarrow{n_1}.\overrightarrow{n_2}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}$.

Ví dụ: Tính số đo góc giữa hai đường thẳng ∆₁và∆₂ trong mỗi trường hợp sau:

a) ∆₁: x + 2y – 5 = 0 và ∆₂: 2x + 3y – 4 = 0;

b) ∆₃: 3x – 2y + 1 = 0 và ∆₄: .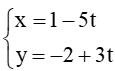

Hướng dẫn giải

a) Đường thẳng ∆₁: x + 2y – 5 = 0 có vectơ pháp tuyến là $\overrightarrow{n_1}$ = (1 ; 2); Đường thẳng ∆₂: 2x + 3y – 4 = 0 có vec tơ pháp tuyến là $\overrightarrow{n_2}$ = (2 ; 3).

Do đó:

cos(∆₁, ∆₂) = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{|\overrightarrow{n_1}.\overrightarrow{n_2}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{|1.2+2.3|}{\sqrt{1^2+2^2}.\sqrt{2^2+3^2}}=\frac{8}{\sqrt{65}}$

⇒ (∆₁, ∆₂) ≈ 7°8’.

Vậy góc giữa hai đường thẳng ∆₁và∆₂ khoảng 7°8’.

b) Đường thẳng ∆₃: 3x – 2y + 1 = 0 có vectơ pháp tuyến là $\overrightarrow{n_3}$ = (3 ; –2) nên có vectơ chỉ phương là $\overrightarrow{u_3}$ = (2 ; 3); Đường thẳng ∆₄ có vec tơ chỉ phương là $\overrightarrow{u_4}$ = (–5 ; 3).

Do đó cos(∆₃, ∆₄) = $\frac{|2.\left(-5\right)+3.3|}{\sqrt{2^2+3^2}.\sqrt{{\left(-5\right)}^2+3^2}}=\frac{1}{\sqrt{442}}$.

⇒ (∆₃, ∆₄) ≈ 87°16’.

12. Khoảng cách từ một điểm đến một đường thẳng

Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ có phương trình ax + by + c = 0 (a² + b² > 0) và điểm M(x₀ ; y₀). Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức sau:

d(M, ∆) = $\frac{|a{x}_0+b{y}_0+c|}{\sqrt{a^2+b^2}}$.

Chú ý: Nếu M ∈ ∆ thì d(M, ∆) = 0.

Ví dụ: Tìm khoảng cách từ điểm M(3; 4) đến đường thẳng ∆: 2x + 6y – 3 = 0.

Hướng dẫn giải

Khoảng cách từ M đến đường thẳng ∆ là d(M, ∆) = $\frac{|2.3+6.4-3|}{\sqrt{2^2+6^2}}=\frac{27}{\sqrt{40}}$.

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là $\frac{27}{\sqrt{40}}$.

13. Phương trình đường tròn

a. Phương trình đường tròn

Nhận xét: Với hai điểm I(a; b) và M(x; y) trong mặt phẳng tọa độ Oxy, ta có:

IM = $\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}$.

* Phương trình chính tắc của đường tròn:

Phương trình đường tròn tâm I(a ; b) bán kính R là (x – a)² + (y – b)² = R².

* Phương trình tổng quát của đường tròn

– Ta có thể viết phương trình (x – a)² + (y – b)² = R² của đường tròn tâm I(a ; b) bán kính R về phương trình có dạng x² + y² – 2ax – 2by + c = 0. Dạng đó thường được gọi là phương trình tổng quát của đường tròn.

– Phương trình có dạng x² + y² – 2ax – 2by + c = 0 là phương trình đường tròn khi và chỉ khi a² + b² > c. Lúc này đường tròn có tâm I(a ; b) bán kính R = $\sqrt{a^2+b^2-c}$.

Ví dụ:

a) Viết phương trình chính tắc của đường tròn tâm I(1 ; 2) và bán kính R= 3;

b) Phương trình x² + y² – 6x + 4y + 5 = 0 có phải là phương trình tổng quát của đường tròn không? Nếu có, hãy tìm tâm và bán kính của đường tròn đó.

Hướng dẫn giải

a) Phương trình chính tắc của đường tròn tâm I(1 ; 2) và bán kính R= 3 là (x – 1)² + (y – 2)² = 3² ⇔ (x – 1)² + (y – 2)² = 9

Vậy phương trình chính tắc của đường tròn tâm I(1 ; 2) và bán kính R= 3 là (x – 1)² + (y – 2)² = 9.

b) Phương trình x² + y² – 6x + 4y + 5 = 0 có dạng x² + y² – 2ax – 2by + c = 0 với a = 3, b = –2, c = 5.

Ta có a² + b² = 3² + (–2)² = 13 > 5 nên a² + b² > c.

Do đó, phương trình x² + y² – 6x + 4y + 5 = 0 là phương trình tổng quát của một đường tròn tâm là I(3 ; –2) và bán kính R = $\sqrt{a^2+b^2-c}$ = $\sqrt{3^2+{\left(-2\right)}^2-5}$ = $\sqrt{8}$.

Vậy phương trình x² + y² – 6x + 4y + 5 = 0 là phương trình tổng quát của một đường tròn tâm là I(3 ; –2) và bán kính R = $\sqrt{8}$.

b. Phương trình đường tròn đi qua ba điểm không thẳng hàng

Có duy nhất một đường tròn đi qua ba điểm không thẳng hàng cho trước nên ta có thể lập được phương trình đường tròn đó khi biết tọa độ của ba điểm nói trên .

Ví dụ: Lập phương trình đường tròn đi qua ba điểm A(0 ; –3), B(1 ; 4), C(2 ; –4).

Hướng dẫn giải

Giả sử tâm của đường tròn là I(a ; b).

Ta có IA = IB = IC ⇔ IA² = IB² = IC².

IA = $\sqrt{{\left(0-a\right)}^2+{\left(-3-b\right)}^2}$ ⇒ IA² = (0 – a)² + (–3 – b)² = a² + b² + 6b + 9.

IB = $\sqrt{{\left(1-a\right)}^2+{\left(4-b\right)}^2}$ ⇒ IB² = (1 – a)² + (4 – b)² = a² + b² – 2a – 8b + 17.

IC = $\sqrt{{\left(2-a\right)}^2+{\left(-4-b\right)}^2}$ ⇒ IC² = (2 – a)² + (–4 – b)² = a² + b² – 4a + 8b + 20.

Vì IA² = IB², IB² = IC² nên:

Suy ra tâm I của đường tròn có tọa độ là $\left(\frac{17}{6};\frac{1}{6}\right)$, bán kính đường tròn

R = IA = $\sqrt{{\left(0-a\right)}^2+{\left(-3-b\right)}^2}$ = $\sqrt{{\left(0-\frac{17}{6}\right)}^2+{\left(-3-\frac{1}{6}\right)}^2}$= $\frac{5\sqrt{26}}{6}$.

Khi đó phương trình đường tròn là ${\left(x-\frac{17}{6}\right)}^2+{\left(y-\frac{1}{6}\right)}^2=\frac{650}{36}$.

Vậy phương trình đường tròn là ${\left(x-\frac{17}{6}\right)}^2+{\left(y-\frac{1}{6}\right)}^2=\frac{650}{36}$.

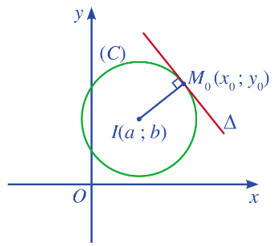
14. Phương trình tiếp tuyến của đường tròn

Cho đường tròn (C) tâm I(a ; b) và điểm M₀(x₀ ; y₀) nằm trên đường tròn đó. Gọi ∆ là tiếp tuyến của đường tròn (C) tại điểm M₀(x₀ ; y₀). Khi đó, ta có:

– Đường thẳng ∆ đi qua điểm M₀(x₀ ; y₀) và có vec tơ pháp tuyến $\overrightarrow{I{M}_0}$ = (x₀ – a ; y₀ – b).

– Phương trình tiếp tuyến ∆ là (x₀ – a)(x – x₀) + (y₀ – b)(y – y₀) = 0.

Ví dụ: Lập phương trình tiếp tuyến của đường tròn (C) : x² + y² – 2x + 4y – 20 = 0 tại điểm M(4; 2).

Hướng dẫn giải

Phương trình của đường tròn (C) : x² + y² – 2x + 4y – 20 = 0 có dạng x² + y² – 2ax – 2by + c = 0, với a = 1, b = –2.

Do đó tâm của đường tròn (C) là I(1 ; –2).

Phương trình tiếp tuyến của (C) tại M(4; 2) có dạng:

(4 – 1)(x – 4) + (2 + 2)(y – 2) = 0 ⇔ 3x + 4y – 20 = 0.

Vậy phương trình tiếp tuyến của (C) tại M(4; 2) là 3x + 4y – 20 = 0.

15. Đường elip

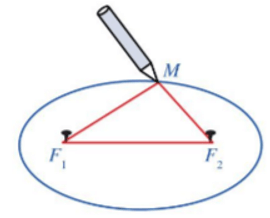
a. Định nghĩa đường elip

Cho hai điểm F₁, F₂ cố định có khoảng cách F₁F₂ = 2c (c > 0)

Đường elip (còn gọi là elip) là tập hợp các điểm M trong mặt phẳng sao cho MF₁ + MF₂ = 2a, trong đó a là số cho trước lớn hơn c.

Hai điểm F₁ và F₂ được gọi là hai tiêu điểm của elip.

b. Phương trình chính tắc của elip

Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF₁ + MF₂ = 2a, ở đó F₁F₂ = 2c (với a > c > 0).

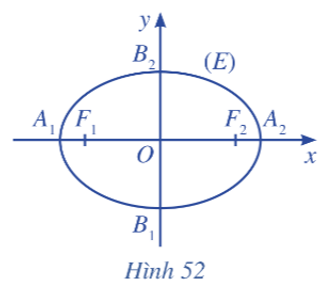
Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của F₁F₂, trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 52). Khi đó, F₁(–c ; 0) và F₂(c ; 0) là hai tiêu điểm của elip (E).

Khi chọn hệ trục tọa độ như trên, phương trình đường elip có thể viết dưới dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, trong đó a > b > 0.

Đây gọi là phương trình chính tắc của elip.

Chú ý: Đối với elip (E) có phương trình chính tắc như đã nêu ở trên, ta có:

+ c² = a² – b², ở đó 2c = F₁F₂.

+ Nếu điểm M(x ; y) thuộc elip (E) thì –a ≤ x ≤ a.

Ví dụ:

a) Phương trình $\frac{x^2}{3^2}+\frac{y^2}{5^2}=1$ có phải là phương trình chính tắc của elip không?

b) Lập phương trình chính tắc của elip (E) có tiêu điểm F₁(–3 ; 0) và đi qua điểm A(0 ; 2).

Hướng dẫn giải

a) Phương trình chính tắc của elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, trong đó a > b > 0.

Mà phương trình $\frac{x^2}{3^2}+\frac{y^2}{5^2}=1$ có a = 3, b = 5 nên a < b.

Suy ra phương trình $\frac{x^2}{3^2}+\frac{y^2}{5^2}=1$ không phải là phương trình chính tắc của elip.

Vậy phương trình $\frac{x^2}{3^2}+\frac{y^2}{5^2}=1$ không phải là phương trình chính tắc của elip.

b) Elip (E) có phương trình chính tắc là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Do F₁(–3; 0) là một tiêu điểm của (E) nên c = 3.

Điểm A(0; 2) ∈ (E) nên ta có: $\frac{0^2}{a^2}+\frac{2^2}{b^2}=1$ ⇔ b² = 2² = 4

Suy ra a² = b² + c² = 4 + 3² = 13

Do đó phương trình elip (E) là $\frac{x^2}{13}+\frac{y^2}{4}=1$.

Vậy phương trình chính tắc của elip (E) có tiêu điểm F₁(–3 ; 0) và đi qua điểm A(0 ; 2) là $\frac{x^2}{13}+\frac{y^2}{4}=1$.

16. Đường hypebol

a. Định nghĩa đường hypebol

Cho hai điểm F₁ và F₂ cố định có khoảng cách F₁F₂ = 2c (c > 0).

Đường hypebol (còn gọi là hypebol) là tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a, trong đó a là số nguyên dương cho trước nhỏ hơn c.

Hai điểm F₁ và F₂ được gọi là hai tiêu điểm của hypebol.

b. Phương trình chính tắc của đường hypebol

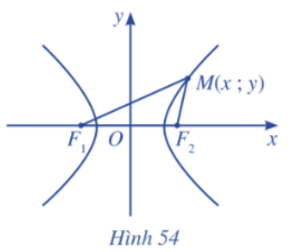
Chọn hệ trục tọa độ tương tự elip, ta chọn Ox là đường thẳng F₁F₂, trục Oy là đường trung trực của đoạn thẳng F₁F₂ = 2c (c > 0), gốc tọa độ O là trung điểm của đoạn thẳng F₁F₂ (Hình 54).

Khi chọn hệ trục tọa độ như trên, phương trình đường hypebol có thể viết dưới dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó a > 0, b > 0.

Đây gọi là phương trình chính tắc của hypebol.

Chú ý: Đối với hypebol (H) có phương trình chính tắc như đã nêu ở trên, ta có:

+ c² = a² + b², ở đó 2c = F₁F₂ và điều kiện a > b là không bắt buộc.

+ Nếu điểm M(x ; y) thuộc hypebol (H) thì x ≤ –a hoặc x ≥ a.

Ví dụ:

a) Phương trình $\frac{x^2}{3^2}-\frac{y^2}{5^2}=1$ có phải là phương trình chính tắc của hypebol không?

b) Lập phương trình chính tắc của hypebol (H) có tiêu điểm F₁(–5 ; 0) và đi qua điểm A(–4 ; 0).

Hướng dẫn giải

a) Phương trình chính tắc của hypebol có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, trong đó a > 0, b > 0.

Mà phương trình $\frac{x^2}{3^2}-\frac{y^2}{5^2}=1$ có a = 3, b = 5 nên $\frac{x^2}{3^2}-\frac{y^2}{5^2}=1$ là phương trình chính tắc của một hypebol.

Vậy phương trình $\frac{x^2}{3^2}-\frac{y^2}{5^2}=1$ là phương trình chính tắc của một hypebol.

b) Hypebol (H) có phương trình chính tắc là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

Do F₁(–5 ; 0) là một tiêu điểm của (H) nên c = 5.

Điểm A(–4 ; 0) ∈ (H) nên ta có: $\frac{{\left(-4\right)}^2}{a^2}-\frac{0^2}{b^2}=1$ ⇔ a² = 16

Suy ra c² = a² + b² ⇔ 5² = 16 + b² ⇔ b² = 9

Do đó phương trình hypebol (H) là $\frac{x^2}{16}-\frac{y^2}{9}=1$.

Vậy phương trình chính tắc của hypebol (H) có tiêu điểm F₁(–5 ; 0) và đi qua điểm A(–4 ; 0) là $\frac{x^2}{16}-\frac{y^2}{9}=1$.

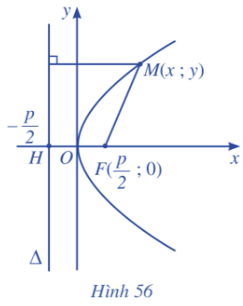
17. Đường parabol

a. Định nghĩa đường parabol

Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F.

Đường parabol (còn gọi là parabol) là tập hợp các điểm M trong mặt phẳng cách đều F và ∆.

Điểm F được gọi là tiêu điểm của parabol. Đường thẳng ∆ được gọi là đường chuẩn của parabol.

b. Phương trình chính tắc của parabol

Cho parabol (P) với tiêu điểm F và đường chuẩn ∆.

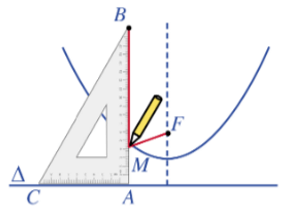
Kẻ FH vuông góc với ∆ (H ∈ ∆). Đặt FH = p > 0.

Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm của đoạn thẳng FH và F nằm trên tia Ox (Hình 56)

Khi chọn hệ trục tọa độ như trên, phương trình đường parabol có thể viết dưới dạng y² = 2px (p > 0).

Đây gọi là phương trình chính tắc của parabol.

Chú ý: Đối với parabol (P) có phương trình chính tắc y² = 2px (p > 0), ta có:

+ Tiêu điểm là $F\left(\frac{p}{2};0\right)$ và phương trình đường chuẩn là: x + $\frac{p}{2}$ = 0.

+ Nếu điểm M(x ; y) thuộc parabol (P) thì x ≥ 0.

Ví dụ:

a) Phương trình y² = –2x có phải là phương trình chính tắc của parabol không?

b) Viết phương trình chính tắc của parabol (P) biết (P) có tiêu điểm là F(4 ; 0).

Hướng dẫn giải

a) Phương trình chính tắc của parabol có dạng y² = 2px (p > 0).

Mặt khác phương trình y² = –2x có dạng y² = 2px với p = –1 < 0.

Suy ra phương trình y² = –2x không phải là phương trình của parabol.

b) Vì (P) có tiêu điểm là F(4 ; 0) nên $\frac{p}{2}$ = 4 ⇒ p = 8.

Do đó phương trình chính tắc của parabol (P) là y² = 2.8.x = 16x.

Vậy phương trình chính tắc của parabol (P) là y² = 16x.

18. Một số ứng dụng thực tiễn của ba đường conic

Ba đường conic có nhiều ứng dụng thực tiễn. Ta nêu ra một vài ứng dụng của ba đường conic

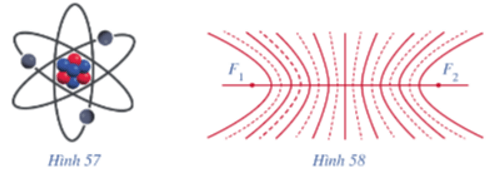
1. Năm 1911, nhà vật lí học người Anh là Emest Rutherford (1871 – 1937) đã đề xuất mô hình hành tinh nguyên tử, trong đó hạt nhân nhỏ bé nằm tại tâm của nguyên tử, còn các electron bay quanh hạt nhân trên các quỹ đạo hình elip như các hành tinh bay quanh Mặt Trời (Hình 57).

2. Trong vật lí, hiện tượng hai sóng gặp nhau tạo nên các gợn sóng ổn định gọi là hiện tượng giao thoa của hai sóng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa (Hình 58).

3. Với gương parabol, tia sáng phát ra từ tiêu điểm (tia tới) chiếu đến một điểm của parabol sẽ bị hắt lại (tia phản xạ) theo một tia song song (hoặc trùng) với trục của parabol (Hình 59).

Tính chất trên có nhiều ứng dụng, chẳng hạn:

– Đèn pha: Bề mặt của đèn phan là một mặt tròn xoay sinh bởi một cung parabol quay quanh trục của nó, bóng đèn được đặt ở vị trí tiêu điểm của parabol đó (Hình 60). Các tia sáng phát ra từ bóng đèn khi chiếu đến bề mặt của đèn pha sẽ bị hắt lại theo các tia sáng song song, cho phép chúng ta quan sát được các vật ở xa.

– Chảo vệ tinhcungx có dạng như đèn pha. Điểm thu và phát tín hiệu của máy được đặt ở vị trí tiêu điểm của parabol (Hình 61).

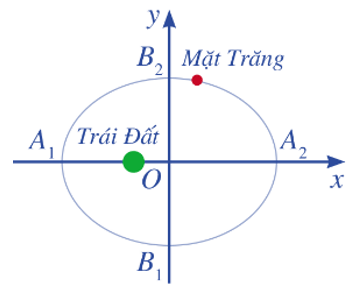
Ví dụ:Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip với tâm Trái Đất là một tiêu điểm. Elip đó có A₁A₂ = 768 800 km và B₁B₂ = 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.

Hướng dẫn giải

Ta có A₁A₂ = 768 800 và B₁B₂ = 767 640 ⇒ 2a = 768 800 và 2b = 767 640

⇒ a = 384 400 và b = 383 820.

Suy ra c² = a² – b² ⇒ c = $\sqrt{a^2-b^2}$ = $\sqrt{{384400}^2-{383820}^2}$ ≈ 21 108.

Vì vậy, khoảng cách lớn nhất từ tâm Trái Đất đến Mặt trăng là:

a + c ≈ 384 400 + 21 108 = 405 508 (km)

Khoảng cách nhỏ nhất từ tâm Trái Đất đến Mặt trăng là:

a – c ≈ 384 400 – 21 108 = 363 292 (km)

Vậy khoảng cách lớn nhất từ tâm Trái Đất đến Mặt trăng khoảng 405 508 km, và khoảng cách nhỏ nhất từ tâm Trái Đất đến Mặt trăng khoảng 363 292 km.

Bài tập tổng hợp Toán 10 Chương 7

Bài 1: Tìm tọa độ của các vec tơ sau:

a) $\overrightarrow{a}$ = 2$\overrightarrow{i}$ + $\overrightarrow{j}$;

b) $\overrightarrow{b}$ = –$\overrightarrow{j}$;

c) $\overrightarrow{c}$ = $\sqrt{2}$$\overrightarrow{i}$ – 1,5$\overrightarrow{j}$.

Hướng dẫn giải

a) Ta có $\overrightarrow{a}$ = 2$\overrightarrow{i}$ + $\overrightarrow{j}$ = 2$\overrightarrow{i}$ + 1$\overrightarrow{j}$

Suy ra $\overrightarrow{a}$ = (2 ; 1).

Vậy $\overrightarrow{a}$ = (2 ; 1).

b) Ta có $\overrightarrow{b}$ = –$\overrightarrow{j}$ = 0$\overrightarrow{i}$ + (–1)$\overrightarrow{j}$

Suy ra $\overrightarrow{b}$ = (0 ; –1).

Vậy $\overrightarrow{b}$ = (0 ; –1).

c) Ta có $\overrightarrow{c}$ = $\sqrt{2}\overrightarrow{i}$ – 1,5$\overrightarrow{j}$ = $\sqrt{2}\overrightarrow{i}$ + (– 1,5)$\overrightarrow{j}$.

Suy ra $\overrightarrow{c}$ = ($\sqrt{2}$; – 1,5).

Vậy $\overrightarrow{c}$ = ($\sqrt{2}$; – 1,5).

Bài 2: Tìm số thực m và n sao cho hai vec tơ $\overrightarrow{a}$ = (m; –4) và $\overrightarrow{b}$ = (–1; 3m + n) bằng nhau.

Hướng dẫn giải

Ta có $\overrightarrow{a}$ = $\overrightarrow{b}$ ⇔

Vậy để $\overrightarrow{a}$ = $\overrightarrow{b}$ thì m = –1 và n = –1.

Bài 3: Cho 3 điểm A(0; 2), B(–1; 3), C(2; 5). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

Hướng dẫn giải

Giả sử điểm D có tọa độ là (x_D ; y_D)

Ta có $\overrightarrow{AB}$ = (–1 – 0 ; 3 – 2) = (–1 ; 1)

$\overrightarrow{DC}$ = (2 – x_D ; 5 – y_D).

Để ABCD là hình bình hành thì $\overrightarrow{AB}$ = $\overrightarrow{DC}$.

$\overrightarrow{AB}$ = $\overrightarrow{DC}$ ⇔

Suy ra điểm D có tọa độ là (3 ; 4).

Vậy để ABCD là hình bình hành thì D(3 ; 4).

Bài 4: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(–2; –3), C(0; 4).

a) Tính $\overrightarrow{AB}$.$\overrightarrow{AC}$

b) Giải tam giác ABC.

Hướng dẫn giải

a) Ta có $\overrightarrow{AB}$ = (–2 – 1 ; –3 – 2) = (–3 ; –5)

$\overrightarrow{AC}$ = (0 – 1 ; 4 – 2) = (–1 ; 2)

Khi đó $\overrightarrow{AB}$.$\overrightarrow{AC}$ = –3.(–1) + (–5). 2 = –7.

Vậy $\overrightarrow{AB}$.$\overrightarrow{AC}$ = –7.

b) Ta có $\overrightarrow{AB}$ = (–3; –5) ⇒ AB = |$\overrightarrow{AB}$| = $\sqrt{{\left(-3\right)}^2+{\left(-5\right)}^2}=\sqrt{34}$.

$\overrightarrow{AC}$ = (–1; 2) ⇒ AC = |$\overrightarrow{AC}$| = $\sqrt{{\left(-1\right)}^2+2^2}=\sqrt{5}$.

$\overrightarrow{BC}$ = (0 – (–2) ; 4 – (–3)) = (2; 7) ⇒ BC = |$\overrightarrow{BC}$| = $\sqrt{2^2+7^2}=\sqrt{53}$.

cos($\overrightarrow{AB}$.$\overrightarrow{AC}$) = $\frac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=\frac{-3.\left(-1\right)+\left(-5\right).2}{\sqrt{34}.\sqrt{5}}=\frac{-7}{\sqrt{170}}$

Suy ra ($\overrightarrow{AB}$.$\overrightarrow{AC}$) ≈ 122^o28’

⇒ $\widehat{BAC}$ ≈ 122^o28’.

Ta có $\overrightarrow{BA}$ = (1 – (–2) ; 2 – (–3)) = (3; 5).

cos($\overrightarrow{BA}$, $\overrightarrow{BC}$) = $\frac{\overrightarrow{BA}.\overrightarrow{BC}}{\left|\overrightarrow{BA}\right|.\left|\overrightarrow{BC}\right|}=\frac{3.2+5.7}{\sqrt{34}.\sqrt{53}}=\frac{41}{\sqrt{1802}}$

Suy ra ($\overrightarrow{BA}$, $\overrightarrow{BC}$) ≈ 15°1’

⇒ $\widehat{ABC}$ ≈15°1’.

Mặt khác $\widehat{ACB}$ = 180^o – ($\widehat{BAC}$+$\widehat{ABC}$) = 42^o31’.

Vậy tam giác ABC có AB = $\sqrt{34}$; AC = $\sqrt{5}$; BC = $\sqrt{53}$; $\widehat{BAC}$ ≈ 122^o28’; $\widehat{ABC}$ ≈15^o1’; $\widehat{ACB}$ = 42^o31’.

Bài 5: $\overrightarrow{u}$ = (2 ; –2) và $\overrightarrow{v}$ = (3 ; 5)

a) Tìm tọa độ của vectơ $\overrightarrow{m}$ = $\overrightarrow{u}$ + $\overrightarrow{v}$.

b) Tìm tọa độ của vectơ $\overrightarrow{n}$ = –3$\overrightarrow{u}$ – $\overrightarrow{v}$.

Hướng dẫn giải

a) Ta có $\overrightarrow{m}$ = $\overrightarrow{u}$ + $\overrightarrow{v}$ = (2 + 3; –2 + 5) = (5 ; 3).

Vậy $\overrightarrow{m}$ = $\overrightarrow{u}$ + $\overrightarrow{v}$ = (5; 3).

b) Ta có $\overrightarrow{n}$ = –3$\overrightarrow{u}$ – $\overrightarrow{v}$ = (–3.2 – 3; –3.(–2) – 5) = (–9; 1).

Vậy $\overrightarrow{n}$ = –3$\overrightarrow{u}$ – $\overrightarrow{v}$ = (–9; 1).

Bài 6: Trong mặt phẳng tọa độ Oxy cho ba điểm A(0; 4), B(–1; 3), C(–5; 2).

a) Tìm tọa độ trung điểm I của đọan thẳng AB.

b) Chứng minh ba điểm A, B, C không thẳng hàng.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

Hướng dẫn giải

a) Gọi tọa độ trung điểm I của đoạn thẳng AB là (x_I; y_I).

Khi đó, vì I là trung điểm của AB nên ta có:

$x_I=\frac{x_A+x_B}{2}=\frac{0+\left(-1\right)}{2}=\frac{-1}{2}$; $y_I=\frac{y_A+y_B}{2}=\frac{4+3}{2}=\frac{7}{2}$.

Suy ra $I\left(\frac{-1}{2};\frac{7}{2}\right)$.

Vậy $I\left(\frac{-1}{2};\frac{7}{2}\right)$.

b) Để chứng minh ba điểm A, B, C không thẳng hàng ta chứng minh $\overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương.

Ta có $\overrightarrow{AB}$ = (–1 – 0 ; 3 – 4) = (–1 ; –1)

$\overrightarrow{AC}$ = (–5 – 0 ; 2 – 4) = (–5 ; –2)

Ta thấy $\frac{-1}{-5}\ne \frac{-1}{-2}$ nên $\overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương

Suy ra ba điểm A, B, C không thẳng hàng.

Vậy ba điểm A, B, C không thẳng hàng.

c) Gọi tọa độ trọng tâm G của tam giác ABC lần lượt là (x_G ; y_G).

Vì G là trọng tâm của tam giác ABC nên ta có:

$x_G=\frac{x_A+x_B+x_C}{3}=\frac{0+\left(-1\right)+\left(-5\right)}{3}=-2$; $y_G=\frac{y_A+y_B+y_C}{3}=\frac{4+3+2}{3}=3$.

Suy ra G(–2 ; 3).

Vậy G(–2 ; 3).

Bài 7: Viết phương trình đường thẳng d biết:

a) Đường thẳng d đi qua điểm M(4; 3) và có vectơ pháp tuyến là $\overrightarrow{n}$ = (3; –4).

b) Đường thẳng d đi qua điểm M(0 ; –2) và có vectơ chỉ phương là $\overrightarrow{u}$ = (1; 1).

c) Đường thẳng d đi qua hai điểm A(–1 ; 3) và B(2 ; –6).

Hướng dẫn giải

a) Phương trình đường thẳng d đi qua điểm M(4; 3) và có vectơ pháp tuyến là $\overrightarrow{n}$ = (3; –4) là: 3(x – 4) – 4.(y – 3) = 0 ⇔ 3x – 4y = 0.

Vậy phương trình của ∆ là 3x – 4y = 0.

b) Phương trình tham số của đường thẳng d đi qua điểm M(0 ; –2) và có vectơ chỉ phương là $\overrightarrow{u}$ = (1; 1) là

Vậy phương trình tham số của đường thẳng d đi qua điểm M(0 ; –2) và có vectơ chỉ phương là $\over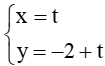rightarrow{u}$ = (1; 1) là .

c) Phương trình d đi qua hai điểm A(–1 ; 3) và B(2 ; –6) là

$\frac{x+1}{2+1}=\frac{y-3}{-6-3}\iff \frac{x+1}{3}=\frac{y-3}{-9}$⇔ 3x + y = 0.

Vậy phương trình đường thẳng ∆ đi qua hai điểm A(–1 ; 3) và B(2 ; –6) là 3x + y = 0.

Bài 8: Cho đường thẳng ∆ có phương trình tổng quát là –x + 7y – 5 = 0.

a) Lập phương trình tham số của đường thẳng ∆.

b) Tìm tọa độ giao điểm của đường thẳng ∆ lần lượt với các trục Ox, Oy.

Hướng dẫn giải

a) Đường thẳng ∆ có phương trình tổng quát là –x + 7y – 5 = 0 nên có vectơ pháp tuyến $\overrightarrow{n}$ = (–1 ; 7).

Suy ra đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u}$ = (7 ; 1).

Ta thấy điểm A(–5 ; 0) thuộc ∆.

Khi đó, phương trình tham số của đường thẳng ∆ đi qua điểm A(–5 ; 0) có vectơ chỉ phương $\over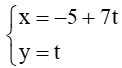rightarrow{u}$ = (7 ; 1) là: .

Vậy phương trình tham số của đường thẳng ∆ là .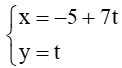

b) Tọa độ giao điểm của ∆ với trục Ox là nghiệm của hệ:

Giải hệ 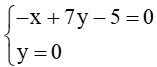ta được

Suy ra tọa độ giao điểm của ∆ với trục Ox là (–5 ; 0).

Tọa độ giao điểm của ∆ với trục Oy là nghiệm của hệ:

Giải hệ 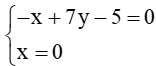ta được

Suy ra tọa độ giao điểm của ∆ với trục Oy là $\left(0;\frac{5}{7}\right)$

Vậy tọa độ giao điểm của ∆ với trục Ox, Oy lần lượt là (–5 ; 0) và $\left(0;\frac{5}{7}\right)$.

Bài 9: Cho tam giác ABC có A(0; 4), B(–3; 2), C(1; 6).

a) Lập phương trình của đường thẳng BC.

b) Lập phương trình đường trung trực của đoạn thẳng AB.

c) Lập phương trình đường trung tuyến AM của tam giác ABC.

Hướng dẫn giải

a) Phương trình đường thẳng BC đi qua hai điểm B(–3; 2), C(1; 6) là

$\frac{x+3}{1+3}=\frac{y-2}{6-2}$ ⇔ $\frac{x+3}{4}=\frac{y-2}{4}$ ⇔ x – y + 5 = 0.

Vậy phương trình đường thẳng BC là x – y + 5 = 0.

b) Gọi I(x_I ; y_I) là trung điểm của AB.

Khi đó $x_I=\frac{x_A+x_B}{2}=\frac{0+\left(-3\right)}{2}=\frac{-3}{2}$; $y_I=\frac{y_A+y_B}{2}=\frac{4+2}{2}=3$.

Suy ra $I\left(\frac{-3}{2};3\right)$.

Đường trung trực của AB đi qua điểm I và nhận vec tơ $\overrightarrow{AB}$ = (–3 ; –2) làm vectơ pháp tuyến.

Khi đó đường trung trực của AB có phương trình là:

–3(x – $\frac{-3}{2}$) – 2(y – 3) = 0 ⇔ –3x – 2y + $\frac{21}{2}$ = 0.

Vậy phương trình đường trung trực của AB là –3x – 2y + $\frac{21}{2}$ = 0.

c) Gọi M(x_M ; y_M) là trung điểm của đoạn thẳng BC.

Khi đó $x_M=\frac{x_B+x_C}{2}=\frac{-3+1}{2}=-1$; $y_M=\frac{y_B+y_C}{2}=\frac{2+6}{2}=4$.

Suy ra M(–1 ; 4).

Đường trung tuyến AM đi qua hai điểm A và có vectơ chỉ phương $\overrightarrow{AM}$ = (–1 ; 0) có phương trình là:

Vậy đường trung tuyến AM có phương trình là .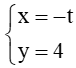

Bài 10: Xét vị trí tương đối của các cặp đường thẳng sau:

a) ∆₁: x – y – 2 = 0 và ∆₂: x + 2y + 1 = 0;

b) ∆₃: –2x – 5y + 6 = 0 và ∆₄:

c) ∆₅: 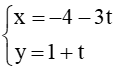và ∆₆:

Hướng dẫn giải

a) Tọa độ giao điểm của đường thẳng ∆₁ và đường thẳng ∆₂ là nghiệm của hệ phương trình

Hệ 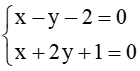có nghiệm duy nhất là

Suy ra ∆₁ và ∆₂ cắt nhau tại điểm có tọa độ (1 ; –1).

Vậy ∆₁ và ∆₂ cắt nhau tại điểm có tọa độ (1 ; –1).

b) Đường thẳng ∆₃: –2x – 5y + 6 = 0 có vectơ pháp tuyến là $\overrightarrow{n_3}$ = (–2 ; –5) nên có vectơ chỉ phương là $\overrightarrow{u_3}$ = (5 ; –2).

Đường thẳng ∆₄ có vectơ chỉ phương là $\overrightarrow{u_4}$ = (–10; 4).

Ta thấy $\overrightarrow{u_4}$ = –2$\overrightarrow{u_3}$ nên $\overrightarrow{u_4}$ và $\overrightarrow{u_3}$ cùng phương.

Khi đó ∆₃ và ∆₄ song song hoặc trùng nhau.

Lấy điểm A(3; 0) thuộc ∆₃, thay tọa độ của A vào phương trình của ∆₄ ta được:

(thỏa mãn).

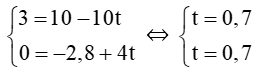
Suy ra A ∈∆₄

Suy ra ∆₃ và ∆₄ trùng nhau.

Vậy ∆₃ và ∆₄ trùng nhau.

c) Đường thẳng ∆₅ có vectơ chỉ phương là $\overrightarrow{u_5}$= (–3 ; 1); đường thẳng ∆₆ có vectơ chỉ phương là $\overrightarrow{u_6}$ = (3 ; –1).

Ta thấy $\overrightarrow{u_5}$ = –1$\overrightarrow{u_6}$ nên $\overrightarrow{u_5}$ và $\overrightarrow{u_6}$ cùng phương

Suy ra ∆₅ và ∆₆ song song hoặc trùng nhau.

Lấy điểm B(–4 ; 1) ∈∆₅. Thay tọa độ của B vào phương trình của ∆₆ ta được:

(vô lý).

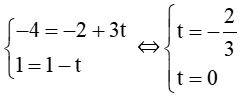
⇒ B ∉∆₆.

Suy ra ∆₅ và ∆₆ song song.

Vậy ∆₅ và ∆₆ song song.

Bài 11: Tìm góc giữa các cặp đường thẳng sau:

a) ∆₁ : x + y – 10 = 0 và ∆₂ : 2x + 99 = 0.

b) d₁: 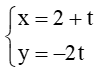và d₂: x – 2y + 3 = 0.

Hướng dẫn giải

a) ∆₁ : x + y – 10 = 0 có vectơ pháp tuyến là $\overrightarrow{n_1}$ = (1 ; 1); Đường thẳng ∆₂ : 2x + 99 = 0 có vectơ pháp tuyến là $\overrightarrow{n_2}$ = (2 ; 0);

cos(∆₁, ∆₂) = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{|\overrightarrow{n_1}.\overrightarrow{n_2}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{|1.2+1.0|}{\sqrt{1^2+1^2}.\sqrt{2^2+0^2}}=\frac{1}{\sqrt{2}}$.

⇒ (∆₁, ∆₂) = 45°.

Vậy góc giữa ∆₁ và ∆₂ bằng 45°.

b) Đường thẳng d₁: 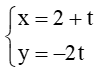có vectơ chỉ phương là $\overrightarrow{u_1}$ = (1 ; –2); đường thẳng d₂: x – 2y + 3 = 0 có vectơ pháp tuyến là $\overrightarrow{n_2}$ = (1; –2) nên có vectơ chỉ phương là $\overrightarrow{u_2}$ = (2; 1).

Khi đó cos(d₁, d₂) = $\frac{|1.2+\left(-2\right).1|}{\sqrt{1^2+{\left(-2\right)}^2}.\sqrt{2^2+1^2}}=\frac{0}{5}=0$.

⇒ (d₁, d₂) = 90°.

Vậy góc giữa d₁ và d₂ bằng 90°.

Bài 12: Tính khoảng cách từ điểm A đến đường thẳng d trong mỗi trường hợp sau:

a) A(3 ; 5) và ∆: 4x + 3y + 1 = 0;

b) A(6 ; –2) và ∆:

Hướng dẫn giải

a) Khoảng cách từ A(3 ; 5) đến đường thẳng ∆ là d(M, ∆) = $\frac{|4.3+3.5+1|}{\sqrt{4^2+3^2}}=\frac{28}{5}$.

Vậy khoảng cách từ điểm A đến đường thẳng ∆ là $\frac{28}{5}$.

b) Thay tọa độ điểm A(6 ; –2) vào phương trình tham số của ∆ ta có:

(thỏa mãn).

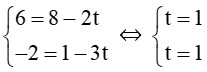
Do đó A ∈ ∆.

Suy ra khoảng cách từ A đến đường thẳng ∆ bằng 0.

Vậy khoảng cách từ A đến đường thẳng ∆ bằng 0.

Bài 13: Phương trình nào sau đây là phương trình đường tròn. Hãy tìm tâm và bán kính của đường tròn đó.

a) x² + y² – x – 7y = 0;

b) x² + y² – 6x + 8y + 100 = 0;

Hướng dẫn giải

a) Phương trình x² + y² – x – 7y = 0 có dạng x² + y² – 2ax – 2by + c = 0, với a = $\frac{1}{2}$, b = $\frac{7}{2}$, c = 0.

Ta có a² + b² = ${\left(\frac{1}{2}\right)}^2+{\left(\frac{7}{2}\right)}^2$ = 12,5 > 0 nên a² + b² > c.

Do đó, phương trình x² + y² – x – 7y = 0 là phương trình tổng quát của một đường tròn tâm là $I\left(\frac{1}{2};\frac{7}{2}\right)$ và bán kính R = $\sqrt{a^2+b^2-c}$ = $\sqrt{{\left(\frac{1}{2}\right)}^2+{\left(\frac{7}{2}\right)}^2-0}$ = $\sqrt{12,5}$.

Vậy phương trình x² + y² – x – 7y = 0 là phương trình tổng quát của một đường tròn tâm là $I\left(\frac{1}{2};\frac{7}{2}\right)$ và bán kính R = $\sqrt{12,5}$.

b) Phương trình x² + y² – 6x + 8y + 100 = 0 có dạng x² + y² – 2ax – 2by + c = 0, với a = 3, b = –4, c = 100.

Ta có a² + b² = 3² + (–4)² = 25 < 100 nên a² + b² < c.

Do đó, phương trình x² + y² – 6x + 8y + 100 = 0 không là phương trình tổng quát của đường tròn.

Vậy phương trình x² + y² – 6x + 8y + 100 = 0 không là phương trình tổng quát của đường tròn.

Bài 14: Lập phương trình đường tròn trong mỗi trường hợp sau:

a) Đường tròn tâm I(–2 ; 3) và bán kính bằng 1.

b) Đường tròn tâm I(0 ; –3) và đi qua điểm A(4; 8).

c) Đường tròn đi qua ba điểm A(1 ; 4) , B(–7 ; 4), C(2 ; –5).

Hướng dẫn giải

a) Phương trình đường tròn tâm I(–2 ; 3) và bán kính bằng 1 có dạng (x + 2)² + (y – 3)² = 1².

Vậy đường tròn tâm I(–2 ; 3) và bán kính bằng 1 có phương trình là (x + 2)² + (y – 3)² = 1.

b) Đường tròn tâm I(0 ; –3) và đi qua điểm A(4; 8) nên bán kính đường tròn này là R = IA = $\sqrt{{\left(4-0\right)}^2+{\left(8+3\right)}^2}$ = $\sqrt{137}$.

Do đó phương trình đường tròn tâm I(0 ; –3) bán kính R = $\sqrt{137}$ là: (x – 0)² + (y + 3)² = 137 ⇔ x² + (y + 3)² = 137.

Vậy phương trình đường tròn tâm I(0 ; –3) và đi qua điểm A(4; 8) là x² + (y + 3)² = 137.

c) Giả sử tâm của đường tròn là I(a ; b). A(1 ; 4) , B(–7 ; 4), C(2 ; –5).

Ta có IA = IB = IC ⇔ IA² = IB² = IC².

IA = $\sqrt{{\left(1-a\right)}^2+{\left(4-b\right)}^2}$ ⇒ IA² = (1 – a)² + (4 – b)² = a² + b² –2a – 8b + 17.

IB = $\sqrt{{\left(-7-a\right)}^2+{\left(4-b\right)}^2}$ ⇒ IB² = (–7 – a)² + (4 – b)² = a² + b² + 14a – 8b + 65.

IC = $\sqrt{{\left(2-a\right)}^2+{\left(-5-b\right)}^2}$ ⇒ IC² = (2 – a)² + (–5 – b)² = a² + b² – 4a + 10b + 29.

Vì IA² = IB², IB² = IC² nên:

Suy ra tâm I của đường tròn có tọa độ là (–3 ; –1), bán kính đường tròn

R = IA = $\sqrt{{\left(1-a\right)}^2+{\left(4-b\right)}^2}$ = $\sqrt{{\left(1+3\right)}^2+{\left(4+1\right)}^2}$ = $\sqrt{41}$.

Khi đó phương trình đường tròn là (x + 3)² + (y + 1)² = 41.

Vậy phương trình đường tròn đi qua ba điểm A(1 ; 4) , B(–7 ; 4), C(2 ; –5) là (x + 3)² + (y + 1)² = 41.

Bài 15: Lập phương trình tiếp tuyến của đường tròn (C): (x – 2)² + (y – 1)² = 5 tại điểm C(2 ; $\sqrt{5}$ + 1).

Hướng dẫn giải

Đường tròn (C) có tâm I(2 ; 1) và bán kính R = $\sqrt{5}$.

Phương trình tiếp tuyến của (C) tại C(2 ; $\sqrt{5}$ + 1) có dạng:

(2 – 2)(x – 2) + ($\sqrt{5}$ + 1 – 1)(y – $\sqrt{5}$ – 1) = 0 ⇔ $\sqrt{5}$y – 5$\sqrt{5}$ – $\sqrt{5}$ = 0.

Vậy phương trình tiếp tuyến của (C) tại C(2 ; $\sqrt{5}$ + 1) là $\sqrt{5}$y – 5$\sqrt{5}$ – $\sqrt{5}$ = 0.

Bài 16: Viết phương trình chính tắc của elip (E) biết một tiêu điểm là (12 ; 0) và điểm (13 ; 0) nằm trên elip.

Hướng dẫn giải

a) Elip (E) có phương trình chính tắc là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Do (12 ; 0) là một tiêu điểm của (E) nên c = 12.

Điểm (13 ; 0) ∈ (E) nên ta có: $\frac{{13}^2}{a^2}+\frac{0^2}{b^2}=1$ ⇔ a² = 13² = 169.

Suy ra a² = b² + c² ⇔ 169 = b² + 12² ⇔ b² = 25.

Do đó phương trình elip (E) là $\frac{x^2}{169}+\frac{y^2}{25}=1$.

Vậy phương trình chính tắc của elip (E) có một tiêu điểm là (12 ; 0) và điểm (13 ; 0) nằm trên elip là $\frac{x^2}{169}+\frac{y^2}{25}=1$.

Bài 17: Cho hypebol (H) có phương trình $\frac{x^2}{16}-\frac{y^2}{20}=1$. Tìm tiêu điểm và tiêu cự của hypebol (H).

Hướng dẫn giải

Từ phương trình của hypebol (H): $\frac{x^2}{16}-\frac{y^2}{20}=1$ta có a² = 16, b² = 20,

Mặt khác c² = a² + b² ⇒ $c=\sqrt{a^2+b^2}=\sqrt{16+20}=\sqrt{36}=6$.

Do đó hypebol (H) có hai tiêu điểm F₁ (–6 ; 0), F₂ (6 ; 0) và có tiêu cự F₁F₂ = 2c = 2.6 = 12.

Vậy hypebol (H) có hai tiêu điểm F₁ (–6 ; 0), F₂ (6 ; 0) và có tiêu cự F₁F₂ = 2c = 2.6 = 12.

Bài 18 : Cho parabol (P): y² = 7x. Tìm tiêu điểm F, đường chuẩn ∆ của (P).

Hướng dẫn giải

Ta có 2p = 7 nên p = $\frac{7}{2}$ ⇒ $\frac{p}{2}=\frac{7}{4}$.

Khi đó parabol có tiêu điểm F($\frac{7}{4}$ ; 0) và đường chuẩn ∆: $x+\frac{7}{4}=0$.

Vậy parabol có tiêu điểm F($\frac{7}{4}$ ; 0) và đường chuẩn ∆: $x+\frac{7}{4}=0$.

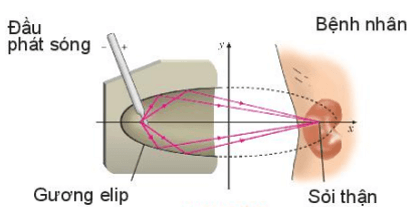
Bài 19: Gương elip trong một máy tán sỏi thận ứng với elip có phương trình chính tắc là $\frac{x^2}{441}+\frac{y^2}{81}=1$ (đơn vị cm)

Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.

Hướng dẫn giải

Từ phương trình của elip $\frac{x^2}{441}+\frac{y^2}{81}=1$ ta có a² = 441, b² = 81.

Khi đó $c=\sqrt{a^2-b^2}=\sqrt{441-81}=\sqrt{360}$ (cm).

Tiêu cự của elip bằng 2c = 2.$\sqrt{360}$ ≈ 38(cm)

Khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán chính là tiêu cự của elip bằng 38 cm.

Vậy khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán chính là 38 cm.

Học tốt Toán 10 Chương 7

Các bài học để học tốt Chương 7 Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài tập cuối chương 7