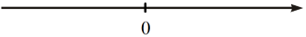Tổng hợp lý thuyết Toán 10 Chương 1 Cánh diều

---

Với tổng hợp lý thuyết Toán lớp 10 Chương 1: Mệnh đề toán học. Tập hợp hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Tổng hợp lý thuyết Toán 10 Chương 1 Cánh diều

Lý thuyết tổng hợp Toán 10 Chương 1

1. Mệnh đề toán học

1.1. Mệnh đề, mệnh đề chứa biến

• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học. Mỗi mệnh đề toán học phải đúng hoặc sai, không thể vừa đúng, vừa sai.

− Khi mệnh đề toán học là đúng, ta gọi mệnh đề đó là một mệnh đề đúng.

− Khi mệnh đề toán học là sai, ta gọi mệnh đề đó là một mệnh đề sai.

• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng/sai. Với mỗi giá trị cụ thể của biến số, ta có thể khẳng định tính đúng/sai của mệnh đề.

Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …

1.2. Mệnh đề phủ định

• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là $\overline{P}$.

Mệnh đề $\overline{P}$ đúng khi P sai, và ngược lại.

Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.

1.3. Mệnh đề kéo theo

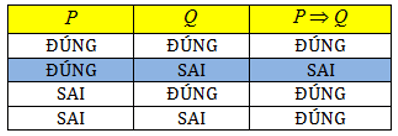
• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.

Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.

Nhận xét: Các định lí toán học thường phát biểu ở dạng mệnh đề kéo theo P ⇒ Q.

Khi đó ta nói:

− P là giả thiết, Q là kết luận của định lí, hoặc

− P là điều kiện đủ để có Q, hoặc Q là điều kiện cần để có P.

1.4. Mệnh đề đảo. Mệnh đề tương đương

• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.

Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.

Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:

+ “P tương đương Q”;

+ “P là điều kiện cần và đủ để có Q”;

+ “P khi và chỉ khi Q”;

+ “P nếu và chỉ nếu Q”.

1.5. Kí hiệu ∀ và ∃

• Kí hiệu ∀ đọc là “với mọi”.

• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).

• Phủ định của mệnh đề “$\forall x\in X,P\left(x\right)$” là mệnh đề “$\exists x\in X,\overline{P\left(x\right)}$”.

• Phủ định của mệnh đề “$\exists x\in X,P\left(x\right)$” là mệnh đề “$\forall x\in X,\overline{P\left(x\right)}$”.

2. Tập hợp và các phép toán trên tập hợp

2.1. Tập hợp

• Tập hợp (còn gọi là tập) là một khái niệm cơ bản trong toán học.

Để chỉ x là một phần tử của tập hợp A, ta viết x ∈ A (đọc là x thuộc A)

Để chỉ x không phải một phần tử của tập hợp A, ta viết x ∉ A (đọc là x không thuộc A)

• Biểu diễn tập hợp bằng một trong 2 cách:

+ Liệt kê các phần tử của tập hợp.

+ Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

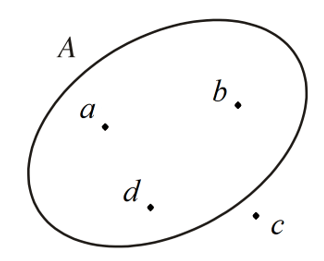
• Minh hoạ tập hợp bằng biểu đồ Ven. Mỗi phần tử thuộc tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp được biểu diễn bởi một chấm bên ngoài vòng kín.

Ở hình dưới, các phần tử thuộc tập hợp A là a, b, d; phần tử không thuộc tập hợp A là c.

• Một tập hợp có thể không có phần tử nào, có một phần tử, có nhiều phần tử, có vô số phần tử. Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng, kí hiệu là $\varnothing$.

Chú ý: Khi C là tập hợp rỗng, ta viết C = $\varnothing$, không được viết $C=\text{{}\varnothing \text{}}$.

2.2. Tập hợp con và tập hợp bằng nhau

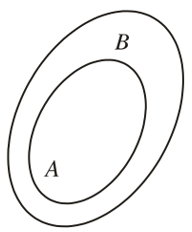
• Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập con của B, kí hiệu là A ⊂ B. Ta còn đọc là A chứa trong B.

Quy ước: Tập hợp rỗng $\varnothing$ là tập con của mọi tập hợp.

Chú ý: + A ⊂ B ⇔ (∀x, x ∈ A ⇒ x ∈ B).

+ Khi A ⊂ B, ta cũng viết B ⊃ A, đọc là B chứa A.

+ Nếu A không phải tập con của B, ta viết A ⊄ B.

Tính chất:  

+ A ⊂ A với mọi tập hợp A.

+ Nếu A ⊂ B và B ⊂ C thì A ⊂ C.

• Khi A ⊂ B và B ⊂ A thì ta nói hai tập hợp A và B bằng nhau, viết là A = B.

2.3. Giao của hai tập hợp

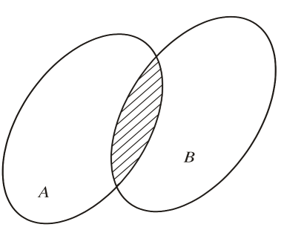
• Tập hợp gồm tất cả các phần tử vừa thuộc A vừa thuộc B được gọi là giao của A và B, kí hiệu A ∩ B.

Vậy A ∩ B = {x | x ∈ A và x ∈ B}.

Tập hợp A ∩ B được minh hoạ bởi phần gạch chéo trong hình dưới.

2.4. Hợp của hai tập hợp:

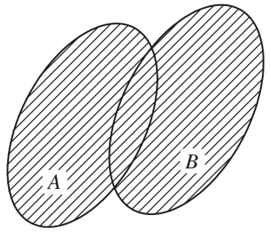
• Tập hợp gồm tất cả các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B, kí hiệu A ∪ B.

Vậy A ∪ B = {x | x ∈ A và x ∈ B}.

Tập hợp A ∩ B được minh hoạ bởi phần gạch chéo trong hình dưới.

2.5. Phần bù và hiệu của hai tập hợp:

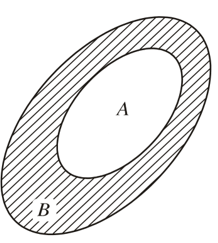
• Cho A ⊂ B. Tập hợp những phần tử của B mà không phải phần tử của A được gọi là phần bù của A trong B, kí hiệu C_BA.

Vậy, khi A ⊂ B ta có C_BA = {x | x ∉ A và x ∈ B}.

Tập hợp C_BA được mô tả bằng phần gạch chéo trong hình dưới.

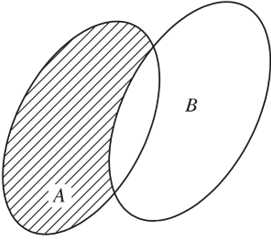
• Tập hợp gồm các phần tử thuộc A nhưng không thuộc B được gọi là hiệu của A và B, kí hiệu A \ B.

Vậy A \ B = {x | x ∈ A và x ∉ B}.

Tập hợp A \ B được minh hoạ bởi phần gạch chéo trong hình dưới.

2.6. Các tập hợp số:

• Các tập hợp ℕ, ℤ, ℚ, ℝ lần lượt là tập hợp số tự nhiên, tập hợp số nguyên, tập hợp số hữu tỉ, tập hợp số thực.

Ta có quan hệ sau: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.

• Một số tập con thường dùng của tập số thực:

Tập hợp	Tên gọi và kí hiệu	Biểu diễn trên trục số
ℝ	Tập hợp số thực (−∞; +∞)
{x ∈ ℝ | a ≤ x ≤ b}	Đoạn [a; b]
{x ∈ ℝ | a < x < b}	Khoảng (a; b)
{x ∈ ℝ | x > a}	Khoảng (a; +∞)
{x ∈ ℝ | x < b}	Khoảng (­−∞; b)
{x ∈ ℝ | a ≤ x < b}	Nửa khoảng [a; b)
{x ∈ ℝ | a < x ≤ b}	Nửa khoảng (a; b]
{x ∈ ℝ | x ≥ a}	Nửa khoảng [a; +∞)
{x ∈ ℝ | x ≤ b}	Nửa khoảng (−∞; b]

 

Kí hiệu −∞ đọc là âm vô cực, kí hiệu +∞ đọc là dương vô cực. a và b là các đầu mút của các đoạn, khoảng, nửa khoảng.

Bài tập tổng hợp Toán 10 Chương 1

Bài 1. Phát biểu phủ định của mệnh đề sau và xét tính đúng sai của nó:

a) P: “15 không chia hết cho 3”

b) Q: “$\sqrt{2}>1$”

Hướng dẫn giải:

a) Mệnh đề phủ định của mệnh đề P là $\overline{P}$: “15 chia hết cho 3”.

Vì 15 = 3.5 nên 15 chia hết cho 3. Do đó $\overline{P}$ là mệnh đề đúng.

b) Mệnh đề phủ định của mệnh đề Q là $\overline{Q}$: “$\sqrt{2}\le 1$”.

Vì $\sqrt{2}\approx 1,41$ > 1 nên $\overline{Q}$ là mệnh đề sai.

Bài 2. Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng/sai của mệnh đề phủ định đó:

a) A: “Phương trình x² + 4x + 5 = 0 có nghiệm”.

b) B: “Số 2048 chia hết cho 3”

c) C: “ ${\left(\sqrt{3}+\sqrt{12}\right)}^2$ là một số hữu tỉ”

d) D: “x = 5 là một nghiệm của phương trình x³ − 4x + 1 = 0”

Hướng dẫn giải:

a) Mệnh đề phủ định của mệnh đề A là $\overline{A}$: “Phương trình x² + 4x + 5 = 0 vô nghiệm”.

Xét: $\Delta \text{'}=2^2-5=-1<0$. Do đó phương trình vô nghiệm.

Mệnh đề $\overline{A}$ là mệnh đề đúng.

b) Mệnh đề phủ định của mệnh đề B là $\overline{B}$: “Số 2048 không chia hết cho 3”.

Do 2 + 0 + 4 + 8 = 14 không chia hết cho 3, nên 2048 không chia hết cho 3

Do đó mệnh đề $\overline{B}$ là mệnh đề đúng.

c) Mệnh đề phủ định của mệnh đề C là $\overline{C}$: “${\left(\sqrt{3}+\sqrt{12}\right)}^2$ không phải số hữu tỉ” hoặc “${\left(\sqrt{3}+\sqrt{12}\right)}^2$ là một số vô tỉ”.

Xét: ${\left(\sqrt{3}+\sqrt{12}\right)}^2=3+2\sqrt{36}+12=21$ là số hữu tỉ.

Mệnh đề $\overline{C}$ là mệnh đề sai.

d) Mệnh đề phủ định của mệnh đề D là $\overline{D}$: “x = 5 không phải là nghiệm của phương trình x³ – 4x + 1 = 0”.

Thay x = 5 vào biểu thức, ta có: 5³ – 4.5 + 1 = 106 ≠ 0.

Do đó mệnh đề $\overline{D}$ là mệnh đề đúng.

Bài 3. Phát biểu các mệnh đề sau, sử dụng khái niệm điều kiện cần và điều kiện đủ:

a) Các số tự nhiên có tận cùng bằng 0 đều chia hết cho 5.

b) Hai tam giác bằng nhau có diện tích bằng nhau.

Hướng dẫn giải

a) Một số tự nhiên có tận cùng bằng 0 là điều kiện đủ để số đó chia hết cho 5.

Một số tự nhiên chia hết cho 5 là điều kiện cần để số đó có tận cùng bằng 0.

b) Điều kiện đủ để hai tam giác có diện tích bằng nhau là hai tam giác đó bằng nhau.

Điều kiện cần để hai tam giác bằng nhau là hai tam giác đó có diện tích bằng nhau.

Bài 4. Xét các mệnh đề P: “x là một số hữu tỉ” và Q: “x² là một số hữu tỉ”.

a) Phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của nó.

b) Phát biểu mệnh đề đảo của mệnh đề trên.

c) Chỉ ra một giá trị của x mà mệnh đề đảo sai.

Hướng dẫn giải:

a) Mệnh đề P ⇒ Q được phát biểu là: “Nếu x là một số hữu tỉ thì x² là một số hữu tỉ”.

Mệnh đề P ⇒ Q là mệnh đề đúng.

b) Mệnh đề đảo Q ⇒ P: “Nếu x² là một số hữu tỉ thì x là một số hữu tỉ”.

c) Ta thấy nếu x² = 3 thì $x=\sqrt{3}$ không phải một số hữu tỉ.

Bài 5. Xét các mệnh đề P: “x² = 1” và Q: “x = 1”.

a) Phát biểu mệnh đề P ⇒ Q và mệnh đề đảo của nó.

b) Xét tính đúng sai của các mệnh đề trên.

Hướng dẫn giải:

a) Mệnh đề P ⇒ Q: “Nếu x² = 1 thì x = 1”.

Mệnh đề đảo Q ⇒ P: “Nếu x = 1 thì x² = 1”.

b) Ta thấy: x² = 1 thì x = 1 hoặc x = −1.

Vậy P ⇒ Q là mệnh đề sai, Q ⇒ P là mệnh đề đúng.

Bài 6. Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng sai của chúng:

a) P(x): “∃x ∈ ℚ: x² = 2”

b) Q(n): “∀n ∈ ℕ, n < 2n”

Hướng dẫn giải:

a) Mệnh đề phủ định $\overline{P\left(x\right)}$: “∀x ∈ ℚ: x² ≠ 2”.

Ta có: x² = 2 ⇔ $\left[\begin{array}{l}x=\sqrt{2}\\ x=-\sqrt{2}\end{array}\right.$, mà $\sqrt{2},-\sqrt{2}$ là các số vô tỉ nên không tồn tại số hữu tỉ nào có bình phương bằng 2, nên $\overline{P\left(x\right)}$ là mệnh đề đúng.

b) Mệnh đề phủ định $\overline{Q\left(n\right)}$: “∃n ∈ ℕ, n ≥ 2n”

Chọn n = 0 thì 2n = 0, khi đó n ≥ 2n. $\overline{Q\left(n\right)}$ là mệnh đề đúng.

Bài 7. Liệt kê các phần tử của tập hợp A các tự nhiên có bình phương nhỏ hơn 90 và tập hợp B các ước số tự nhiên của 30. Xác định các tập hợp A ∩ B, A ∪ B, A \ B, B \ A.

Hướng dẫn giải:

Tập hợp A là tập các số tự nhiên có bình phương nhỏ hơn 90 nên A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9};                          

Tập hợp B là tập các ước số tự nhiên của 30 nên B = {1; 2; 3; 5; 6; 10; 15; 30}.

Khi đó:

A ∩ B = {0; 1; 2; 3; 5; 6}

A ∪ B = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 15; 30}

A \ B = {0; 4; 7; 8; 9}

B \ A = {10; 15; 30}

Bài 8. Biết P là tập hợp các số tự nhiên lớn hơn 15 và là ước số của 60. Biểu diễn tập hợp P bằng hai cách và tìm tất cả các tập hợp con của nó.

Hướng dẫn giải

Theo cách nêu tính chất đặc trưng, ta có: P = {x ∈ ℕ: x >15 và 60 ⋮ x}.

Ta có: 60 = 2².3.5

Suy ra tập các ước số tự nhiên của 60 là Ư(60) = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60}.

Trong đó các ước số tự nhiên lớn hơn 15 là: 20; 30; 60.

Do đó theo cách liệt kê: P = {20; 30; 60}

Các tập hợp con của P là:

$\varnothing$, {20}, {30}, {60}, {20; 30}, {20; 60}, {30; 60}, {20; 30; 60}.

Bài 9. Xác định mỗi tập hợp số sau và biểu diễn nó trên trục số:

a) A = [−3; 3) ∪ (−1; 4);                                         

b) B = (−1; 3) ∩ [0; 5]

c) C = ℝ \ (5; +∞);                                                  

d) D = (−2; 2] ∩ [1; 3)

Hướng dẫn giải

a) Ta có: [−3; 3) = {x ∈ $ℝ$| − 3 ≤ x < 3} và (−1; 4) = {x ∈ $ℝ$| − 1 < x < 4}

⇒ A = [−3; 3) ∪ (−1; 4) = {x ∈ $ℝ$| − 3 ≤ x < 4}

⇒ A = [−3; 4) và được biểu diễn là:

b) Ta có: (−1; 3) = {x ∈ $ℝ$| − 1 < x < 3} và [0; 5] = {x ∈ $ℝ$| − 1 ≤ x ≤ 4}

⇒ B = (−1; 3) ∩ [0; 5] = {x ∈ $ℝ$| − 1 < x < 3}

⇒B = [0; 3) và được biểu diễn là:

c) Tập hợp C biểu diễn những phần tử thuộc tập số thực $ℝ$ nhưng không thuộc tập (5; +∞) nên C = (−∞; 5] và được biểu diễn là:

d) Ta có: D = (−2; 2] = {x ∈ $ℝ$| − 2 < x ≤ 2}và [1; 3) = {x ∈ $ℝ$| 1 ≤ x < 3}

⇒ D = (−2; 2] ∩ [1; 3) = {x ∈ $ℝ$| 1 ≤ x ≤ 2}

⇒ D = [1; 2] và được biểu diễn là:

Bài 10. Tìm các tập hợp sau:

a) A = (−3; 5] ∩ ℤ

b) B = (−3; 5] ∩ ℕ

c) C = C_ℝℚ

d) D = C_ℕ2ℕ (với kí hiệu 2ℕ là tập hợp các số tự nhiên chẵn)

Hướng dẫn giải:

a) A là tập hợp các số nguyên lớn hơn −3 và nhỏ hơn hoặc bằng 5 và

⇒ A = {−2, −1, 0, 1, 2, 3, 4, 5}.

b) B là tập hợp các số tự nhiên lớn hơn −3 và nhỏ hơn hoặc bằng 5

⇒ B = {0, 1, 2, 3, 4, 5}.

c) C là tập hợp các số thực nhưng không phải số hữu tỉ

⇒ C là tập hợp các số vô tỉ.

 d) D là tập hợp các số tự nhiên không phải số chẵn

⇒ D = {1; 3; 5; 7; 9; …}

Bài 11. Xác định tập hợp A \ B, trong đó:

a) A = ℝ;      B = (−∞; 3)

b) A = [1; 5];                   B = (−3; 3) ∪ (2; 4)

c) A = (−5; 0) ∪ (3; 5);              B = (−1; 4) ∩ (2; 6)

Hướng dẫn giải:

a) Ta có: A \ B = ℝ \ (−∞; 3) = [3; +∞)

b) Ta có: A = [1; 5]

B = (−3; 3) ∪ (2; 4) = (−3; 4)

⇒ A \ B = [1; 5] \ (−3; 4) = [4; 5]

c) Ta có: A = (−5; 0) ∪ (3; 5)

B = (−1; 4) ∩ (2; 6) = (2; 4)

⇒ A \ B = (−5; 0) ∪ (3; 5) \ (2; 4) = (−5; 0) ∪ [4; 5)

Bài 12. Những quan hệ trong các quan hệ sau là đúng:

a) A ⊂ (A ∪ B)

b) A ⊂ (A ∩ B)

c) (A ∩ B) ⊂ (A ∪ B)

Hướng dẫn giải:

a) Chọn phần tử x ∈ A. Có 2 trường hợp xảy ra:

+ Nếu x ∈ B thì x ∈ (A ∪ B).

+ Nếu x ∉ B thì ta vẫn có x ∈ (A ∪ B).

Suy ra: ∀x ∈ A thì x ∈ (A ∪ B).

Vậy A ⊂ (A ∪ B) là quan hệ đúng.

b) Chọn phần tử x ∈ A sao cho x ∉ B. Như vậy, x ∉ (A ∩ B)

Vậy A ⊄ (A ∩ B). Khẳng định ban đầu là sai.

c) Với mọi phần tử x ∈ (A ∩ B) thì x ∈ A, suy ra x ∈ (A ∪ B).

Vậy (A ∩ B) ⊂ (A ∪ B) là quan hệ đúng.

Bài 13. Gọi M là tập nghiệm của phương trình x² – 2x – 3 = 0 và N là tập nghiệm của phương trình (x + 1)(2x – 4) = 0.

Tìm các tập hợp M ∩ N, M ∪ N, M \ N.

Hướng dẫn giải:

Lần lượt giải các phương trình:

+) x² – 2x – 3 = 0

⇔ (x + 1)(x – 3) = 0       

⇔ x = − 1 hoặc x = 3

Suy ra:  M = {− 1; 3}

+) (x + 1)(2x – 4) = 0

⇔ x = 1 hoặc x = 2

Suy ra:  N = {1; 2}

Vậy:

M ∩ N = ∅

M ∪ N = {− 1; 2; 3}

M \ N = {3}

Bài 14. Lớp 10A có 15 học sinh giỏi, 20 học sinh được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa học lực giỏi vừa có hạnh kiểm tốt. Hỏi lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải đạt học lực giỏi hoặc có hạnh kiểm tốt?

Hướng dẫn giải:

Gọi G là tập hợp các bạn đạt học lực giỏi, T là tập hợp các bạn đạt hạnh kiểm tốt. Số học sinh được khen thưởng là số phần tử của tập hợp G ∪ T.

Ta đếm số phần tử của G (15 bạn), sau đó đếm số phần tử của T (20 bạn). Nhưng khi đó số phần tử của G ∩ T (10 bạn) lại được đếm 2 lần.

Vậy số phần tử của G ∪ T là 15 + 20 – 10 = 25. Có 25 bạn được khen thưởng.

Bài 15. Lớp 10B có 40 học sinh, trong đó 28 bạn chơi biết đá bóng và 19 bạn biết chơi cờ vua. Biết rằng có 10 bạn biết chơi cả 2 môn. Hỏi có bao nhiêu bạn không biết chơi cả bóng đá và cờ vua?

Hướng dẫn giải:

Gọi A là tập hợp các bạn biết đá bóng, B là tập hợp các bạn biết chơi cờ vua. Số học sinh biết chơi cả hai môn là số phần tử của tập hợp G ∪ T.

Ta đếm số phần tử của A (28 bạn), sau đó đếm số phần tử của B (19 bạn). Nhưng khi đó số phần tử của A ∩ B (10 bạn) lại được đếm 2 lần.

Suy ra số bạn biết ít nhất một trong 2 môn (số phần tử của A ∪ B) là 28 + 19 – 10 = 37.

Vậy, có 40 – 37 = 3 bạn không biết chơi cả bóng đá và cờ vua.

Học tốt Toán 10 Chương 1

Các bài học để học tốt Chương 1 Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài tập cuối chương 1