Tích của một số với một vectơ (Lý thuyết Toán lớp 10) - Cánh diều

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 5: Tích của một số với một vectơ sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Trắc nghiệm Toán 10 Bài 5: Tích của một số với một vectơ (có đáp án)

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Tích của một số với một vectơ

1. Định nghĩa

Cho một số k ≠ 0 và vectơ $\vec{a}$ ≠ $\vec{0}$ . Tích của một số k với vectơ $\vec{a}$ là một vectơ, kí hiệu là $k \vec{a}$ , được xác định như sau:

+ cùng hướng với $\vec{a}$ nếu k > 0, ngược hướng với $\vec{a}$ nếu k < 0;

+ có độ dài bằng |k|.| $\vec{a}$ |.

Quy ước: $0 \vec{a} = \vec{0}, k \vec{0} = \vec{0}$ .

Phép lấy tích của một số với một vecto gọi là phép nhân một số với một vecto.

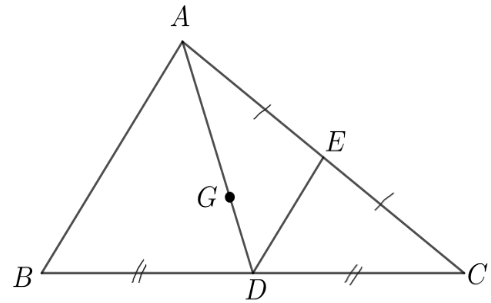
Ví dụ:Cho G là trọng tâm của tam giác ABC, D và E lần lượt là trung điểm của BC và AC. Tìm mối quan hệ của $\vec{G A}$ và $\vec{G D}$ ; mối quan hệ của $\vec{A D}$ và $\vec{G D}$ .

Hướng dẫn giải

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) | Cánh diều

Khi đó ta có:

- Vì G là trọng tâm của tam giác ABC nên GA = 2GD.

Mà G nằm giữa A và D nên $\vec{G A}$ và $\vec{G D}$ là hai vecto ngược hướng.

⇒ $\vec{G A} = (- 2) \vec{G D}$ .

- Ta có: AD = 3GD.

Mà $\vec{G D}$ và $\vec{A D}$ là hai vecto cùng hướng.

⇒ $\vec{A D} = 3 \vec{G D}$ .

Ví dụ: Cho vecto $\vec{a}$ có | $\vec{a}$ | = 4. Tìm số thực x sao cho vecto $x \vec{a}$ có độ dài bằng 1 và cùng hướng với $\vec{a}$ .

Hướng dẫn giải:

Ta có: | $x \vec{a}$ | = 1 ⟺ | $x$ |.| $\vec{a}$ | = 1 ⟺ | $x$ |.4 = 1

⟺ |x| = $\frac{1}{4}$

Lại có vecto x $\vec{a}$ cùng hướng với vecto $\vec{a}$ nên x > 0

Suy ra x = $\frac{1}{4}$ .

Vậy x = $\frac{1}{4}$ là giá trị cần tìm.

2. Tính chất

Với hai vecto bất kì $\vec{a}$ , $\vec{b}$ và hai số thực h, k, ta có:

+) k( $\vec{a} + \vec{b}$ ) = k $\vec{a}$ + k $\vec{b}$ ; k( $\vec{a} - \vec{b}$ ) = k $\vec{a}$ - k $\vec{b}$ ;

+) (h + k) $\vec{a}$ = h $\vec{a}$ + k $\vec{a}$ ;

+) h(k $\vec{a}$ ) = (hk) $\vec{a}$ ;

+) 1 $\vec{a}$ = $\vec{a}$ ; (-1) $\vec{a}$ = - $\vec{a}$ .

Nhận xét: k $\vec{a}$ = $\vec{0}$ khi và chỉ khi k = 0 hoặc $\vec{a} = \vec{0}$ .

Ví dụ: Tính:

a) $5 \vec{B C} + 5 \vec{C A}$ ;

b) $4 \vec{A B} + 6 \vec{A B}$ ;

c) $4 (2 \vec{A B}) + 2 \vec{B C} - 3 \vec{A B}$ .

Hướng dẫn giải:

a) $5 \vec{B C} + 5 \vec{C A}$ = 5( $\vec{B C} + \vec{C A}$ ) = 5 $\vec{B A}$ .

b) $4 \vec{A B} + 6 \vec{A B}$ = (4 + 6) $\vec{A B}$ = 10 $\vec{A B}$ .

c) $4 (2 \vec{A B}) + 2 \vec{B C} - 3 \vec{A B}$

= (4.2) $\vec{A B}$ + 5 $\vec{B C}$ - 3 $\vec{A B}$

= $8 \vec{A B} + 5 \vec{B C} - 3 \vec{A B}$

= $8 \vec{A B} - 3 \vec{A B} + 5 \vec{B C}$

= (8 – 3) $\vec{A B}$ + 5 $\vec{B C}$

= 5 $\vec{A B}$ + 5 $\vec{B C}$

= 5( $\vec{A B} + \vec{B C}$ ) = 5 $\vec{A C}$

3. Một số ứng dụng

3.1. Trung điểm của đoạn thẳng

Nếu I là trung điểm của đoạn thẳng AB thì $\vec{M A} + \vec{M B} = 2 \vec{M I}$ với điểm M bất kì.

Chứng minh:

Vì I là trung điểm của đoạn thẳng AB nên $\vec{I A} + \vec{I B} = \vec{0}$

Suy ra:

$\vec{M A} + \vec{M B} = (\vec{M I} + \vec{I A}) + (\vec{M I} + \vec{I B}) = \vec{M I} + \vec{I A} + \vec{M I} + \vec{I B} = 2 \vec{M I} + \vec{I A} + \vec{I B}$

$= 2 \vec{M I} + \vec{0} = 2 \vec{M I}$ .

⇒ $\vec{M A} + \vec{M B} = 2 \vec{M I}$ (đpcm).

Ví dụ: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC, BD. Chứng minh $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 2 \vec{M N}$ .

Hướng dẫn giải:

Vì M, N lần lượt là trung điểm của AC, BD nên ta có:

$\vec{M A} + \vec{M C} = \vec{0}$

$\vec{M B} + \vec{M D} = 2 \vec{M N}$

$\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = (\vec{M A} + \vec{M C}) + (\vec{M B} + \vec{M D}) = \vec{0} + 2 \vec{M N} = 2 \vec{M N}$

⇒ $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 2 \vec{M N}$ (đpcm).

3.2. Trọng tâm của tam giác

Nếu G là trọng tâm của tam giác ABC thì $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ với điểm M bất kì.

Ví dụ: Gọi G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’. Chứng minh rằng: $\vec{A A'} + \vec{B B'} + \vec{C C'} = 3 \vec{G G'}$ .

Hướng dẫn giải:

Vì G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’ nên:

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ và $\vec{G A'} + \vec{G B'} + \vec{G C'} = \vec{0}$

Theo quy tắc cộng vecto ta có:

$\vec{A A'} = \vec{A G} + \vec{G G'} + \vec{G' A'}$ (1)

$\vec{B B'} = \vec{B G} + \vec{G G'} + \vec{G' B'}$ (2)

$\vec{C C'} = \vec{C G} + \vec{G G'} + \vec{G' C'}$ (3)

Cộng vế với vế của (1), (2) và (3) ta có:

$\vec{A A'} + \vec{B B'} + \vec{C C'} = 3 \vec{G G'} + (\vec{A G} + \vec{B G} + \vec{C G}) + (\vec{G A'} + \vec{G B'} + \vec{G C'})$

= $3 \vec{G G'} + (- \vec{G A} - \vec{G B} - \vec{G C}) + (\vec{G A'} + \vec{G B'} + \vec{G C'})$

= $3 \vec{G G'} - (\vec{G A} + \vec{G B} + \vec{G C}) + (\vec{G A'} + \vec{G B'} + \vec{G C'})$

= $3 \vec{G G'} + \vec{0} + \vec{0} = 3 \vec{G G'}$

⇒ $\vec{A A'} + \vec{B B'} + \vec{C C'} = 3 \vec{G G'}$ (đpcm).

3.3. Điều kiện để hai vecto cùng phương. Điều kiện để ba điểm thẳng hàng.

- Điều kiện cần và đủ để hai vecto $\vec{a}$ và $\vec{b}$ ( ≠ 0) cùng phương là có một số thực k để $\vec{a} = k \vec{b}$ .

- Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để $\vec{A B} = k \vec{A C}$ .

Nhận xét: Trong mặt phẳng, cho hai vecto $\vec{a}$ và $\vec{b}$ không cùng phương. Với mỗi vecto $\vec{c}$ có duy nhất cặp số (x; y) thoả mãn $\vec{c} = x \vec{a} + y \vec{b}$ .

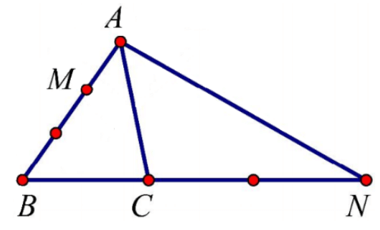
Ví dụ: Cho tam giác ABC. Đặt $\vec{a} = \vec{A B}$ , $\vec{b} = \vec{A C}$ . Dựng các điểm M, N sao cho $\vec{A M} = \frac{1}{3} \vec{A B}$ ; $\vec{C N} = 2 \vec{B C}$ .

a) Phân tích $\vec{C M}$ , $\vec{A N}$ theo các vecto $\vec{a}$ và $\vec{b}$ .

b) Gọi I là điểm thỏa mãn: $\vec{M I} = \vec{C M}$ . Chứng minh I, A, N thẳng hàng.

Hướng dẫn giải:

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) | Cánh diều

a) Ta có:

+) $\vec{C M} = \vec{C A} + \vec{A M} = - \vec{A C} + \frac{1}{3} \vec{A B} = \frac{1}{3} \vec{a} - \vec{b}$ .

+) Vì $\vec{C N} = 2 \vec{B C}$ ⇒ CN = 2BC ⇒ BC = $\frac{1}{3}$ BN ⇒ BN = 3BC.

⟹ $\vec{B N} = 3 \vec{B C}$ .

⇒ $\vec{A N} = \vec{A B} + \vec{B N} = \vec{A B} + 3 \vec{B C} = \vec{A B} + 3 (\vec{A C} - \vec{A B}) = \vec{A B} + 3 \vec{A C} - 3 \vec{A B}$

= $- 2 \vec{A B} + 3 \vec{A C} = - 2 \vec{a} + 3 \vec{b}$ .

b) Ta có:

$\vec{A I} = \vec{A M} + \vec{M I} = \frac{1}{3} \vec{A B} + \vec{C M} = \frac{1}{3} \vec{a} + \frac{1}{3} \vec{a} - \vec{b} = \frac{2}{3} \vec{a} - \vec{b} = - \frac{1}{3} (- 2 \vec{a} + 3 \vec{b})$

⇒ $\vec{A I} = - \frac{1}{3} \vec{A N}$ .

⇒ I, A, N thẳng hàng.

Bài tập Tích của một số với một vectơ

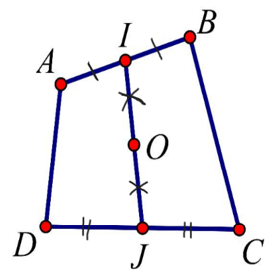
Bài 1:Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ. Chứng minh rằng: $\vec{M A} + \vec{M B} + \overset{⇀}{M C} + \vec{M D} = 4 \vec{M O}$ với M là điểm bất kì.

Hướng dẫn giải:

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) | Cánh diều

Ta có:

$\vec{O A} + \vec{O B} = 2 \vec{O I}$ (Do I là trung điểm của AB)

$\vec{O C} + \vec{O D} = 2 \vec{O J}$ (Do J là trung điểm của CD)

Mặt khác O là trung điểm IJ nên $\vec{O I} + \vec{O J} = \vec{0}$

⇒ $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = 2 \vec{O I} + 2 \vec{O J} = 2 (\vec{O I} + \vec{O J}) = \vec{0}$

Với mọi điểm M, ta lại có:

$\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$

⟺ $(\vec{O M} + \vec{M A}) + (\vec{O M} + \vec{M B}) + (\vec{O M} + \vec{M C}) + (\vec{O M} + \vec{M D}) = \vec{0}$

⟺ $4 \vec{O M} + \vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{0}$

⟺ $(- 4) \vec{M O} + \vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{0}$

⟺ $\vec{M A} + \vec{M B} + \overset{⇀}{M C} + \vec{M D} = 4 \vec{M O}$ (đpcm).

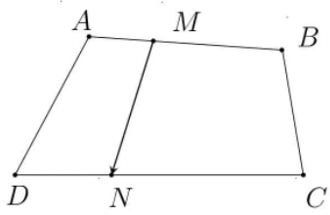
Bài 2: Cho tứ giác ABCD. Gọi M, N lần lượt thuộc các đoạn thẳng AB, CD sao cho MB = 2MA và NC = 2ND. Chứng minh rằng: $\vec{M N} = \frac{2}{3} \vec{A D} + \frac{1}{3} \vec{B C}$ .

Hướng dẫn giải:

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) | Cánh diều

Áp dụng quy tắc cộng vecto, ta có:

$\vec{M N} = \vec{M A} + \vec{A D} + \vec{D N}$ (1)

$\vec{M N} = \vec{M B} + \vec{B C} + \vec{C N}$ (2)

Nhân hai vế của phương trình (1) với 2 ta có:

$2 \vec{M N} = 2 \vec{M A} + 2 \vec{A D} + 2 \vec{D N}$ (3)

Cộng hai vế của (2) và (3) ta có:

$3 \vec{M N} = \vec{M B} + \vec{B C} + \vec{C N} + 2 \vec{M A} + 2 \vec{A D} + 2 \vec{D N}$

⟺ $3 \vec{M N} = (2 \vec{M A} + \vec{M B}) + 2 \vec{A D} + \vec{B C} + (2 \vec{D N} + \vec{C N})$

Vì M, N lần lượt thuộc các đoạn thẳng AB, CD (M, N lần lượt nằm giữa đoạn thẳng AB và CD).

⇒ $\vec{M A}, \vec{M B}$ và $\vec{D N}, \vec{C N}$ là hai cặp vecto ngược hướng.

Mà MB = 2MA và NC = 2ND nên ta có:

$2 \vec{M A} + \vec{M B} = \vec{0}$

$2 \vec{D N} + \vec{C N} = \vec{0}$

Suy ra:

$3 \vec{M N} = 2 \vec{A D} + \vec{B C}$

⇒ $\vec{M N} = \frac{2}{3} \vec{A D} + \frac{1}{3} \vec{B C}$ (đpcm).

Bài 3: Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vecto $\vec{A N}, \vec{M N}, \vec{A G}$ qua các vecto $\vec{A B}$ và $\vec{A C}$ .

Hướng dẫn giải:

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) | Cánh diều

+ Vì ABCD là hình bình hành nên $\vec{B A} = \vec{C D}$

Ta lại có: CD = 2CN nên N là trung điểm của CD.

Mà $\vec{C D}$ và $\vec{C N}$ là hai vecto cùng hướng.

⇒ $\vec{C D} = 2 \vec{C N}$ .

⇔ $\vec{C N} = \frac{1}{2} \vec{C D} \Leftrightarrow \vec{C N} = \frac{1}{2} \vec{B A} \Leftrightarrow \vec{C N} = - \frac{1}{2} \vec{A B}$

Suy ra :

$\vec{A N} = \vec{A C} + \vec{C N} = \vec{A C} - \frac{1}{2} \vec{A B}$

+ Ta có: AB = 3AM ⇒ AM = $\frac{1}{3}$ AB

Mà $\vec{A M}$ và $\vec{A B}$ là hai vecto cùng hướng.

⇒ $\vec{A M} = \frac{1}{3} \vec{A B}$

⇒ $\vec{M A} = - \frac{1}{3} \vec{A B}$

⇒ $\vec{M N} = \vec{M A} + \vec{A N} = - \frac{1}{3} \vec{A B} + (\vec{A C} - \frac{1}{2} \vec{A B}) = - \frac{5}{6} \vec{A B} + \vec{A C}$

Vì G là trọng tâm tam giác MNB nên:

$3 \vec{A G} = \vec{A M} + \vec{A N} + \vec{A B} = \frac{1}{3} \vec{A B} + \vec{A C} - \frac{1}{2} \vec{A B} + \vec{A B} = \frac{5}{6} \vec{A B} + \vec{A C}$

⇒ $\vec{A G} = \frac{5}{18} \vec{A B} + \frac{1}{3} \vec{A C}$

Vậy:

$\vec{A N} = \vec{A C} - \frac{1}{2} \vec{A B}$

$\vec{M N} = - \frac{5}{6} \vec{A B} + \vec{A C}$

$\vec{A G} = \frac{5}{18} \vec{A B} + \frac{1}{3} \vec{A C}$

Bài 4: Cho tam giác ABC có P là trung điểm của AB và hai điểm M, N thỏa mãn các hệ thức: $\vec{M B} = 2 \vec{M C}; \vec{A N} = 2 \vec{N C}$ .

Chứng minh ba điểm M, N, P thẳng hàng.

Hướng dẫn giải:

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) | Cánh diều

Vì:

+) $\vec{A N} = 2 \vec{N C}$

Nên AN = 2NC ⇒ CN = $\frac{1}{3}$ CA.

Mà $\vec{C N}$ và $\vec{C A}$ là hai vecto cùng hướng.

⟹ $\vec{C N} = \frac{1}{3} \vec{C A}$ .

+) $\vec{M B} = 2 \vec{M C}$ ⇒ MB = 2MC ⇒ C là trung điểm của MB.

⟹ MC = CB

Mà $\vec{M C}$ và $\vec{C B}$ là hai vecto cùng hướng.

⇒ $\vec{M C} = \vec{C B}$

⇒ $\vec{M N} = \vec{M C} + \vec{C N} = \vec{C B} + \frac{1}{3} \vec{C A}$

⇒ $3 \vec{M N} = 3 \vec{C B} + \vec{C A}$ (1)

Ta lại có:

+) C là trung điểm của MB ⇒ $\vec{M B} = 2 \vec{C B}$

+) P là trung điểm của AB ⇒ $\vec{B P} = \frac{1}{2} \vec{B A}$

⟹ $\vec{M P} = \vec{M B} + \vec{B P} = 2 \vec{C B} + \frac{1}{2} \vec{B A} = 2 \vec{C B} + \frac{1}{2} (\vec{C A} - \vec{C B}) = 2 \vec{C B} + \frac{1}{2} \vec{C A} - \frac{1}{2} \vec{C B}$

= $\frac{3}{2} \vec{C B} + \frac{1}{2} \vec{C A}$

⟹ $2 \vec{M P} = 3 \vec{C B} + \vec{C A}$ (2)

Từ (1) và (2) ta có:

$3 \vec{M N} = 2 \vec{M P}$ ⟺ $\vec{M N} = \frac{2}{3} \vec{M P}$

Do đó ba điểm M, N, P thẳng hàng (đpcm).

Học tốt Tích của một số với một vectơ

Các bài học để học tốt Tích của một số với một vectơ Toán lớp 10 hay khác:

Giải sgk Toán 10 Bài 5: Tích của một số với một vectơ

Xem thêm tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Lý thuyết Toán 10 Cánh diều

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) - Cánh diều

Tích của một số với một vectơ (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Tích của một số với một vectơ

Bài tập Tích của một số với một vectơ

Học tốt Tích của một số với một vectơ

Xem thêm tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác: