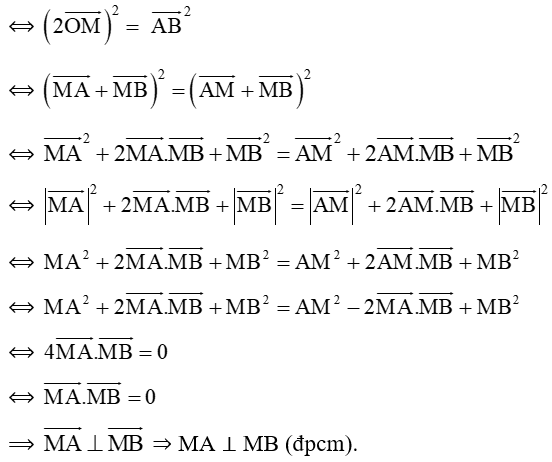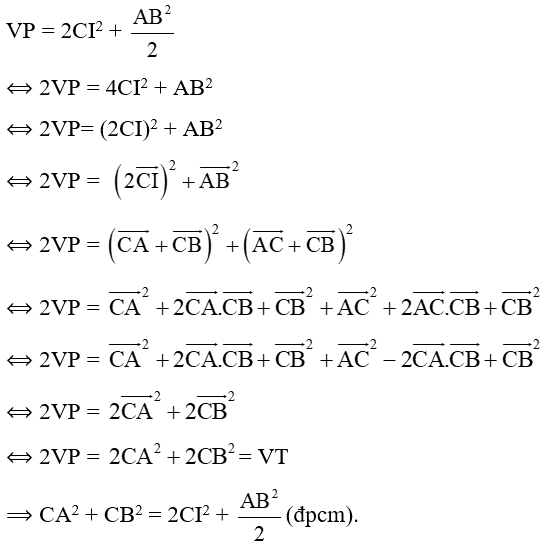Tích vô hướng của hai vectơ (Lý thuyết Toán lớp 10) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 6: Tích vô hướng của hai vectơ sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Tích vô hướng của hai vectơ (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Tích vô hướng của hai vectơ

1. Định nghĩa

1.1. Tích vô hướng của hai vectơ có cùng điểm đầu

- Góc giữa hai vecto $\overrightarrow{OA}$, $\overrightarrow{OB}$ là góc giữa hai tia OA, OB và được kí hiệu là $\left(\overrightarrow{OA},\overrightarrow{OB}\right)$

- Tích vô hướng của hai vecto $\overrightarrow{OA}$ và $\overrightarrow{OB}$ là một số thực, kí hiệu là $\overrightarrow{OA}.\overrightarrow{OB}$, được xác định bởi công thức: $\overrightarrow{OA}$.$\overrightarrow{OB}$=|$\overrightarrow{OA}$|.|$\overrightarrow{OB}$|.cos$\left(\overrightarrow{OA},\overrightarrow{OB}\right)$.

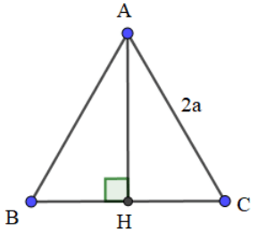
Ví dụ: Cho tam giác ABC đều cạnh 2a có đường cao AH. Tính tích vô hướng của $\overrightarrow{AB}.\overrightarrow{AC}$.

Hướng dẫn giải:

Vì tam giác ABC đều nên $\widehat{BAC}$= 60°

⇒ $\left(\overrightarrow{AB},\overrightarrow{AC}\right)$ = $\widehat{BAC}$ = 60°

Ta có:

$\overrightarrow{AB}.\overrightarrow{AC}$ = |$\overrightarrow{AB}$|.|$\overrightarrow{AC}$|.cos$\left(\overrightarrow{AB},\overrightarrow{AC}\right)$

⇒ $\overrightarrow{AB}.\overrightarrow{AC}$ = AB.AC.cos$\widehat{BAC}$ = AB.AC.cos60° = 2a.2a.$\frac{1}{2}$ = 2a².

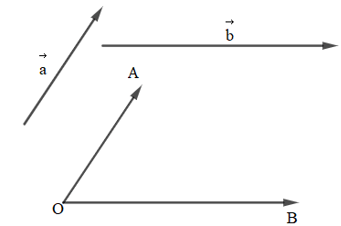
1.2. Tích vô hướng của hai vectơ tùy ý

Định nghĩa:

Cho hai vecto $\overrightarrow{a}$, $\overrightarrow{b}$ khác $\overrightarrow{0}$. Lấy một điểm O và vẽ vecto $\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$(Hình vẽ).

+ Góc giữa hai vecto $\overrightarrow{a}$, $\overrightarrow{b}$, kí hiệu $\left(\overrightarrow{a},\overrightarrow{b}\right)$, là góc giữa hai vecto $\overrightarrow{OA}$, $\overrightarrow{OB}$.

+ Tích vô hướng của hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu $\overrightarrow{a}.\overrightarrow{b}$là tích vô hướng của hai vecto $\overrightarrow{OA}$và $\overrightarrow{OB}$. Như vậy, tích vô hướng của hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ là một số thực được xác định bởi công thức: $\overrightarrow{a}.\overrightarrow{b}=$|$\overrightarrow{a}$|.|$\overrightarrow{b}$|.cos$\left(\overrightarrow{a},\overrightarrow{b}\right)$.

Quy ước: Tích vô hướng của một vecto bất kì với vecto là số 0.

Chú ý:

+) $\left(\overrightarrow{a},\overrightarrow{b}\right)=\left(\overrightarrow{b},\overrightarrow{a}\right)$

+) Nếu $\left(\overrightarrow{a},\overrightarrow{b}\right)$ = 90° thì ta nói hai vecto $\overrightarrow{a}$, $\overrightarrow{b}$ vuông góc với nhau, kí hiệu $\overrightarrow{a}$⊥$\overrightarrow{b}$ hoặc $\overrightarrow{b}$⊥$\overrightarrow{a}$. Khi đó $\overrightarrow{a}.\overrightarrow{b}=$|$\overrightarrow{a}$|.|$\overrightarrow{b}$|.cos$90°=0$.

+) Tích vô hướng của hai vecto cùng hướng bằng tích hai độ dài của chúng.

+) Tích vô hướng của hai vecto ngược hướng bằng số đối của tích hai độ dài của chúng.

Ví dụ: Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng $\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{AC}.\overrightarrow{CB}$.

Hướng dẫn giải:

+ Vì tam giác ABC vuông cân, mà AB = AC

⇒ Tam giác ABC vuông cân tại A.

⇒ AB ⊥ AC

⇒ $\overrightarrow{AB}.\overrightarrow{AC}$ = |$\overrightarrow{AB}$|.|$\overrightarrow{AC}$|.cos$90°$ = |$\overrightarrow{AB}$|.|$\overrightarrow{AC}$|.0 = 0

+ Ta có: BC = $\sqrt{A{B}^2+A{C}^2}$ = $\sqrt{a^2+a^2}$= a$\sqrt{2}$.

⇒ $\overrightarrow{AC}.\overrightarrow{CB}$ = |$\overrightarrow{AC}$|.|$\overrightarrow{CB}$|cos$\left(\overrightarrow{AC},\overrightarrow{CB}\right)$ = a. a$\sqrt{2}$.cos135°

= a. a$\sqrt{2}$.$\left(\frac{-\sqrt{2}}{2}\right)$= -a².

2. Tính chất

Với hai vecto bất kì $\overrightarrow{a}$, $\overrightarrow{b}$ và số thực k tùy ý, ta có:

+) $\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}$(tính chất giao hoán);

+) $\overrightarrow{a}.\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$(tính chất phân phối);

+) $\left(k\overrightarrow{a}\right)\overrightarrow{b}=k\left(\overrightarrow{a}.\overrightarrow{b}\right)=\overrightarrow{a}.\left(k\overrightarrow{b}\right)$;

+) ${\overrightarrow{a}}^2$ ≥ 0, ${\overrightarrow{a}}^2$ = 0 ⟺ $\overrightarrow{a}=\overrightarrow{0}$.

Trong đó, kí hiệu $\overrightarrow{a}.\overrightarrow{a}={\overrightarrow{a}}^2$và biểu thức này được gọi là bình phương vô hướng của vecto .

Ví dụ: Cho 4 điểm A, B, C, D bất kì. Chứng minh: $\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{CA}.\overrightarrow{BD}=\overrightarrow{0}$.

Hướng dẫn giải:

Ta có:

$\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}.\left(\overrightarrow{CA}+\overrightarrow{AD}\right)=\overrightarrow{AB}.\overrightarrow{CA}+\overrightarrow{AB}.\overrightarrow{AD}$ (tính chất phân phối)

$\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{AD}.\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{BA}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AD}=-\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AD}$ (tính chất phân phối)

$\overrightarrow{CA}.\overrightarrow{BD}=\overrightarrow{CA}.\left(\overrightarrow{BA}+\overrightarrow{AD}\right)=\overrightarrow{CA}.\overrightarrow{BA}+\overrightarrow{CA}.\overrightarrow{AD}=-\overrightarrow{CA}.\overrightarrow{AB}-\overrightarrow{AC}.\overrightarrow{AD}$ (tính chất phân phối)

$\Rightarrow \overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{CA}.\overrightarrow{BD}$

$=\overrightarrow{AB}.\overrightarrow{CA}+\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{CA}.\overrightarrow{AB}-\overrightarrow{AC}.\overrightarrow{AD}$

$=\left(\overrightarrow{AB}.\overrightarrow{CA}-\overrightarrow{CA}.\overrightarrow{AB}\right)+\left(\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}\right)+\left(\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AC}.\overrightarrow{AD}\right)$ (tính chất giao hoán và kết hợp)

= 0

⟺ $\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{CA}.\overrightarrow{BD}=\overrightarrow{0}$(đpcm).

3. Một số ứng dụng

3.1. Tính độ dài của đoạn thẳng

Nhận xét:

Với hai điểm A, B phân biệt, ta có: ${\overrightarrow{AB}}^2=|\overrightarrow{AB}{|}^2$.

Do đó độ dài đoạn thẳng AB được tính như sau: AB = $\sqrt{{\overrightarrow{AB}}^2}$

3.2. Chứng minh hai đường thẳng vuông góc

Nhận xét:

+ Cho hai vecto bất kì $\overrightarrow{a}$và $\overrightarrow{b}$khác vecto $\overrightarrow{0}$. Ta có: $\overrightarrow{a}.\overrightarrow{b}$ = 0⟺$\overrightarrow{a}$⊥$\overrightarrow{b}$.

Hai đường thẳng AB và CD vuông góc với nhau khi và chỉ khi $\overrightarrow{AB}.\overrightarrow{CD}=0$

+ Hai đường thẳng a và b vuông góc khi và chỉ khi $\overrightarrow{u}.\overrightarrow{v}=0$, trong đó $\overrightarrow{u}$≠ 0, $\overrightarrow{v}$≠ 0, giá của vecto $\overrightarrow{u}$ song song hoặc trùng với đường thẳng a và giá của vecto $\overrightarrow{v}$ song song hoặc trùng với đường thẳng b.

Ví dụ: Cho hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ vuông góc với nhau và |$\overrightarrow{a}$| = 1, |$\overrightarrow{b}$| = $\sqrt{2}$. Chứng minh hai vecto $2\overrightarrow{a}-\overrightarrow{b}$và $\overrightarrow{a}+\overrightarrow{b}$ vuông góc với nhau.

Hướng dẫn giải:

Vì $\overrightarrow{a}$ và $\overrightarrow{b}$ vuông góc với nhau ⟺ $\overrightarrow{a}.\overrightarrow{b}=0$.

Ta có:

$\left(2\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=2{\overrightarrow{a}}^2+2\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{b}-{\overrightarrow{b}}^2=2{\overrightarrow{a}}^2+\overrightarrow{a}.\overrightarrow{b}-{\overrightarrow{b}}^2$

$=2|\overrightarrow{a}{|}^2+\overrightarrow{a}.\overrightarrow{b}-|\overrightarrow{b}{|}^2$

= 2.1² + 0 - ${\left(\sqrt{2}\right)}^2$= 0

Vì tích của hai vecto $2\overrightarrow{a}-\overrightarrow{b}$và $\overrightarrow{a}+\overrightarrow{b}$bằng 0 nên chúng vuông góc với nhau.

Bài tập Tích vô hướng của hai vectơ

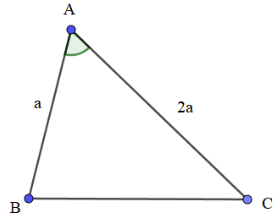
Bài 1: Cho tam giác ABC, biết AB = a, AC = 2a, $\hat{A}$ = 60°. Sử dụng các kiến thức về vecto, tính độ dài cạnh BC.

Hướng dẫn giải:

Áp dụng quy tắc hiệu hai vecto ta có:

$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$

⟹ ${\overrightarrow{BC}}^2={\left(\overrightarrow{AC}-\overrightarrow{AB}\right)}^2={\overrightarrow{AC}}^2-2\overrightarrow{AC}.\overrightarrow{AB}+{\overrightarrow{AB}}^2$

Ta có:

${\overrightarrow{AC}}^2=|\overrightarrow{AC}{|}^2$ = AC² = (2a)² = 4a²

${\overrightarrow{AB}}^2=|\overrightarrow{AB}{|}^2$ = AB² = a²

$\overrightarrow{AC}.\overrightarrow{AB}$= |$\overrightarrow{AC}$|.|$\overrightarrow{AB}$|.cos$\left(\overrightarrow{AC},\overrightarrow{AB}\right)$= AC.AB.cos$\widehat{BAC}$

= 2a.a.cos60° = 2.a.a.$\frac{1}{2}$= a²

⟹ ${\overrightarrow{BC}}^2$= 4a² – 2a² + a² = 3a²

⟹ BC² = $|\overrightarrow{BC}{|}^2$ = ${\overrightarrow{BC}}^2$= 3a²

⟹ BC = $\sqrt{3a^2}$= $a\sqrt{3}$.

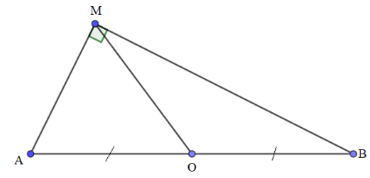
Bài 2: Cho đoạn thẳng AB có trung điểm O, điểm M tùy ý khác O, A, B và không thuộc AB, biết 4OM² = AB². Sử dụng các kiến thức về vecto, chứng minh MA ⊥ MB.

Hướng dẫn giải:

Ta có:

4OM² = AB² ⟺(2OM)² = AB²

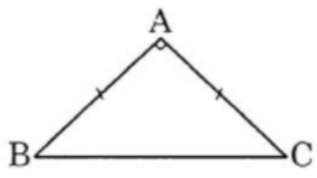
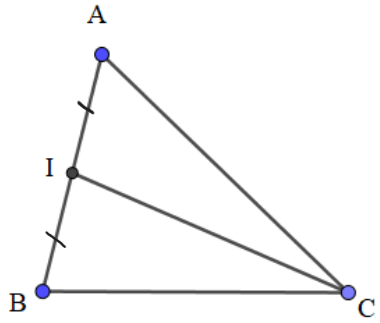
Bài 3: Cho tam giác ABC bất kì có I là trung điểm của AB. Chứng minh đẳng thức:

CA² + CB² = 2CI² + $\frac{A{B}^2}{2}$.

Hướng dẫn giải:

Ta có:

Học tốt Tích vô hướng của hai vectơ

Các bài học để học tốt Tích vô hướng của hai vectơ Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài 6: Tích vô hướng của hai vectơ