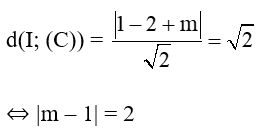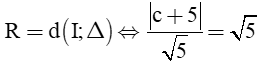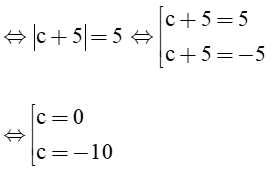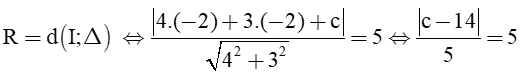15 Bài tập Phương trình đường tròn (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Phương trình đường tròn Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Phương trình đường tròn (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Câu 1. Tọa độ tâm I và bán kính R của đường tròn C : x − 1 2 + y + 3 2 = 25
A. I (– 1; 3), R = 4;
B. I (1; – 3), R = 5;
C. I (1; – 3), R = 16;
D. I (– 1; 3), R = 16.
Hiển thị đáp án
Đáp án đúng là: B
Ta có: C : x − 1 2 + y + 3 2 = 16
⇒ 25
Câu 2. Cho đường tròn C : x 2 + y + 4 2 = 4
A. a + b = c;
B. a + b = – 2c;
C. a – 2b = c;
D.a – 2b = – 2c.
Hiển thị đáp án
Đáp án đúng là: B
Ta có: C : x 2 + y + 4 2 = 4
⇒ R = 4
⇒ a = 0, b = – 4, c = 2
Khi đó ta có nhận xét: a + b = 0 + (– 4) = – 4 = – 2c.
Câu 3. Cho phương trình x2 + y2 – 2ax – 2by + c = 0. Điều kiện của a, b, c để phương trình đã cho là phương trình đường tròn:
A. a2 + b2 > c2 ;
B. c2 > a2 + b2 ;
C. a2 + b2 > c;
D. c > a2 + b2 .
Hiển thị đáp án
Đáp án đúng là: C
Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn khi a2 + b2 > c.
Câu 4. Tọa độ tâm I và bán kính R của đường tròn (C): x2 + y2 = 16 là:
A. I (0; 0), R = 9;
B. I (0; 0), R = 81;
C. I (1; 1), R = 3;
D. I (0; 0), R = 4;
Hiển thị đáp án
Đáp án đúng là: D
Ta có:(C): x2 + y2 = 16
⇒ 16
Câu 5. Đường tròn (C): x2 + y2 – 8x + 2y + 6 = 0 có tâm I, bán kính R lần lượt là:
A. I (3; – 1), R = 4;
B. I (– 3; 1), R = 4;
C. I (4; – 1), R = 11
D. I (– 3; 1), R = 2.
Hiển thị đáp án
Đáp án đúng là: C
Ta có:(C): x2 + y2 – 8x + 2y + 6 = 0⇔ x2 + y2 – 2.4x – 2.(– 1)y + 6 = 0
⇒a = 4; b = – 1 và c = 6
⇒I (4; – 1), R = 3 2 + − 1 2 − 6 = 11
Câu 6. Đường tròn có tâm trùng với gốc tọa độ, bán kính R = 1 có phương trình là:
A. x 2 + y + 1 2 = 1 ;
B. x 2 + y 2 = 1 ;
C. x − 1 2 + y − 1 2 = 1 ;
D. x + 1 2 + y + 1 2 = 1.
Hiển thị đáp án
Đáp án đúng là: B
Đường tròn (C) phải thoả mãn hai điều kiện sau:
2 + y2 = 1 thoả mãn yêu cầu.
Câu 7. Đường tròn có tâm I (1; 2), bán kính R = 2 có phương trình là:
A. x2 + y2 – 2x – 4y + 1 = 0;
B. x2 + y2 + 2x – 4y – 4 = 0;
C. x2 + y2 – 2x + 4y – 4 = 0;
D. x2 + y2 – 2x – 4y – 4 = 0
Hiển thị đáp án
Đáp án đúng là: A
Đường tròn có tâm I (1; 2), bán kính R = 2 có phương trình là :
(x – 1)2 + (y – 2)2 = 4
⇔ x2 + y2 – 2x – 4y + 1 = 0
Câu 8. Đường tròn (C)đi qua ba điểm A (– 1; – 2), B(0; 1) và C(1; 2) có phương trình là:
A. (x – 4)2 + (y – 2)2 = 52 ;
B. (x – 4)2 + (y + 2)2 = 52 ;
C. (x + 4)2 + (y + 2)2 = 52 ;
D. (x + 4)2 + (y – 2)2 = 52 .
Hiển thị đáp án
Đáp án đúng là: B
Gọi phương trình đường tròn cần tím có dạng (C): x2 + y2 + 2ax + 2by + c = 0.
Vì (C) đi qua các điểm A, B, C nên lần lượt thay tọa độ các điểm vào phương trình (C) ta được hệ phương trình:
Vậy phương trình đường tròn (C) là x2 + y2 – 8x + 4y – 5 = 0 ⇔ (x – 4)2 + (y + 2)2 = 52 .
Câu 9. Đường tròn (C) có tâm I (– 2; 3) và đi qua M (2; – 3) có phương trình là:
A. x + 2 2 + y − 3 2 = 52 ;
B. x − 2 2 + y + 3 2 = 52 ;
C. x 2 + y 2 + 4 x − 6 y − 57 = 0 ;
D. x 2 + y 2 + 4 x − 6 y − 39 = 0.
Hiển thị đáp án
Đáp án đúng là: D
Ta có: Bán kính của đường tròn:
R = IM = 2 + 2 2 + − 3 − 3 2 = 52
Vậy phương trình đường tròn 2 + (y – 3)2 = 52
hay x2 + y2 + 4x – 6y – 39 = 0.
Câu 10. Đường tròn đường kính AB với A (3; – 1), B (1; – 5) có phương trình là:
A. (x + 2)2 + (y – 3)2 = 5;
B. (x + 1)2 + (y + 2)2 = 17;
C. (x – 2)2 + (y + 3)2 = 5
D. (x – 2)2 + (y + 3)2 = 5;
Hiển thị đáp án
Đáp án đúng là: D
Ta có: Bán kính của đường tròn là:
R = 1 2 A B 1 2 1 − 3 2 + − 5 + 1 2 5
Khi đó phương trình đường tròn
(C): (x – 2)2 + (y + 3)2 = 5.
Câu 11. Phương trình tiếp tuyến d của đường tròn (C): (x + 2)2 + (y + 2)2 = 9 tại điểm M (2; 1) là:
A. d: – y + 1 = 0;
B. d: 4x + 3y + 14 = 0;
C. d: 3x – 4y – 2 = 0;
D. d: 4x + 3y – 11 = 0.
Hiển thị đáp án
Đáp án đúng là: D
Đường tròn (C) có tâm I (– 2; – 2) nên tiếp tuyến tại M có VTPT là n → = I M → = 4 ; 3 ⇔
Câu 12. Cho đường tròn (C): (x – 1)2 + (y + 2)2 = 2. Viết phương trình tiếp tuyến d của (C) biết đường d song song với đường thẳng d’: x + y + 3 = 0.
A. d: x + y + 1 = 0;
B. d: x –y –1 = 0;
C. d: x + y – 1 = 0;
D. d: x + y + 3 = 0.
Hiển thị đáp án
Đáp án đúng là: C
Đường tròn (C) có tâm I (1; – 2) và bán kính R = 2
Phương trình đường thẳng d // d’ nên có dạng x + y + m = 0 (m ≠ 3).
Vì d là tiếp tuyến của đường tròn (C) nên khoảng cách từ tâm I đến đường thẳng d bằng bán kính của đường tròn. Do đó ta có:
⇔ m – 1 = 2 hoặc m – 1 = – 2
⇔ m = 3 (không thỏa mãn) hoặc m = – 1 (thỏa mãn).
Vậy phương trình tiếp tuyến cần tìm là x + y – 1 = 0.
Câu 13. Phương trình tiếp tuyến d của đường tròn (C): x2 + y2 – 3x – y = 0 tại điểm N(1; – 1) là:
A. d: x + 3y – 2 = 0;
B. d: x – 3y + 4 = 0;
C. d: x – 3y – 4 = 0;
D. d: x + 3y + 2 = 0.
Hiển thị đáp án
Đáp án đúng là: D
Xét phương trình (C): x2 + y2 – 3x – y = 0 ⇔ x − 3 2 2 + y − 1 2 2 = 5 2
Khi đó đường tròn (C) có tâm I 3 2 ; 1 2
n → = I N → = − 1 2 ; − 3 2 = − 1 2 1 ; 3 ,
Nên có phương trình là: 1(x – 1) +3(y + 1) = 0⇔
Câu 14. Viết phương trình tiếp tuyến của đường tròn (C): (x – 3)2 + (y + 1)2 = 5, biết tiếp tuyến song song với đường thẳng d: 2x + y + 7 = 0.
A. 2x + y + 1 = 0 hoặc 2x + y – 1 = 0;
B. 2x + y = 0 hoặc 2x + y – 10 = 0;
C. 2x + y + 10 = 0 hoặc 2x + y – 10 = 0;
D. 2x + y = 0 hoặc 2x + y + 10 = 0.
Hiển thị đáp án
Đáp án đúng là: B
Đường tròn (C) có tâmI(3; –1), R = 5 ∆
Ta có:
Bán kính của đường tròn
suy ra:∆ ∆
Câu 15. Viết phương trình tiếp tuyến của đường tròn C : x 2 + y 2 + 4 x + 4 y − 17 = 0
biết tiếp tuyến vuông góc đường thẳng d: 3x – 4y – 2018 = 0.
A. 3x – 4y + 39 = 0 hoặc 3x – 4y – 11 = 0;
B. 4x + 3y + 39 = 0 hoặc 3x – 4y – 11 = 0;
C. 3x – 4y + 39 = 0 hoặc 4x + 3y – 11 = 0;
D. 4x + 3y + 39 = 0 hoặc 4x + 3y – 11 = 0.
Hiển thị đáp án
Đáp án đúng là: D
Xét phương trình đường thẳng d có VTPT là n d → = u d → =
Vì phương trình tiếp tuyến vuông góc với đường thẳng d nên nhận u d → =
Ta có: Đường tròn (C) có tâm I(– 2; – 2), R = 5
Bán kính đường tròn:
Suy ra có hai phương trình tiếp tuyến thỏa mãn: 4x + 3y + 39 = 0 hoặc ∆
Câu 1:
Tọa độ tâm I và bán kính R của đường tròn \[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 25\] là:
A. I (– 1; 3), R = 4;
B. I (1; – 3), R = 5;
C. I (1; – 3), R = 16;
D. I (– 1; 3), R = 16.
Xem lời giải »
Câu 2:
Cho đường tròn \[\left( C \right):{x^2} + {\left( {y + 4} \right)^2} = 4\] có tọa độ tâm I(a; b) và bán kính R = c . Nhận xét nào sau đây đúng về a, b và c :
A. a + b = c ;
B. a + b = – 2c;
D. a – 2b = – 2c.
Xem lời giải »
Câu 3:
Cho phương trình x2 + y2 – 2ax – 2by + c = 0. Điều kiện của a, b, c để phương trình đã cho là phương trình đường tròn :
B. c2 > a2 + b2 ;
C. a2 + b2 > c;
D. c > a2 + b2 .
Xem lời giải »
Câu 4:
Tọa độ tâm I và bán kính R của đường tròn (C): x2 + y2 = 16 là:
A. I (0; 0), R = 9;
B. I (0; 0), R = 81;
C. I (1; 1), R = 3;
D. I (0; 0), R = 4;
Xem lời giải »
Câu 5:
Đường tròn (C): x2 + y2 – 8x + 2y + 6 = 0 có tâm I, bán kính R lần lượt là:
A. I (3; – 1), R = 4;
B. I (– 3; 1), R = 4;
C. I (4; – 1), R = \[\sqrt {11} \] ;
D. I (– 3; 1), R = 2.
Xem lời giải »
Câu 6:
Đường tròn có tâm trùng với gốc tọa độ, bán kính R = 1 có phương trình là:
A. \[{x^2} + {\left( {y + 1} \right)^2} = 1;\]
B. \[{x^2} + {y^2} = 1;\]
C. \[{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1;\]
D. \[{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 1.\]
Xem lời giải »
Câu 7:
Đường tròn có tâm I (1; 2) , bán kính R = 2 có phương trình là:
A. x2 + y2 – 2x – 4y + 1 = 0;
B. x2 + y2 + 2x – 4y – 4 = 0;
C. x2 + y2 – 2x + 4y – 4 = 0;
D. x2 + y2 – 2x – 4y – 4 = 0
Xem lời giải »
Câu 8:
Đường tròn (C) đi qua ba điểm A (– 1; – 2) , B(0; 1) và C(1; 2) có phương trình là:
A. (x – 4)2 + (y – 2)2 = 52 ;
B. (x – 4)2 + (y + 2)2 = 52 ;
C. (x + 4)2 + (y + 2)2 = 52 ;
D. (x + 4)2 + (y – 2)2 = 52 .
Xem lời giải »
Câu 9:
Đường tròn (C) có tâm I (– 2; 3) và đi qua M (2; – 3) có phương trình là:
A. \[{\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} = \sqrt {52} ;\]
B. \[{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 52;\]
C. \[{x^2} + {y^2} + 4x - 6y - 57 = 0;\]
D. \[{x^2} + {y^2} + 4x - 6y - 39 = 0.\]
Xem lời giải »
Câu 10:
Đ ường tròn đường kính AB với A (3; – 1), B (1; – 5) có phương trình là:
A. (x + 2)2 + (y – 3)2 = 5;
B. (x + 1)2 + (y + 2)2 = 17;
C. (x – 2)2 + (y + 3)2 = \(\sqrt 5 \) ;
D. (x – 2)2 + (y + 3)2 = 5;
Xem lời giải »
Câu 11:
Phương trình tiếp tuyến d của đường tròn (C): (x + 2)2 + (y + 2)2 = 9 tại điểm M (2; 1) là:
A. d: – y + 1 = 0;
B. d: 4x + 3y + 14 = 0;
C. d: 3x – 4y – 2 = 0;
D. d: 4x + 3y – 11 = 0.
Xem lời giải »
Câu 12:
Cho đường tròn (C): (x – 1)2 + (y + 2)2 = 2. Viết phương trình tiếp tuyến d của (C) biết đường d song song với đường thẳng d’: x + y + 3 = 0.
A. d: x + y + 1 = 0 ;
B. d: x – y – 1 = 0;
C. d: x + y – 1 = 0;
D. d: x + y + 3 = 0.
Xem lời giải »
Câu 13:
Phương trình tiếp tuyến d của đường tròn (C): x2 + y2 – 3x – y = 0 tại điểm N(1; – 1) là:
A. d: x + 3y – 2 = 0 ;
B. d: x – 3y + 4 = 0;
C. d: x – 3y – 4 = 0;
D. d: x + 3y + 2 = 0.
Xem lời giải »
Câu 14:
Viết phương trình tiếp tuyến của đường tròn (C): (x – 3)2 + (y + 1)2 = 5, biết tiếp tuyến song song với đường thẳng d: 2x + y + 7 = 0 .
A. 2x + y + 1 = 0 hoặc 2x + y – 1 = 0;
B. 2x + y = 0 hoặc 2x + y – 10 = 0;
C. 2x + y + 10 = 0 hoặc 2x + y – 10 = 0;
D. 2x + y = 0 hoặc 2x + y + 10 = 0 .
Xem lời giải »
Câu 15:
Viết phương trình tiếp tuyến của đường tr òn \[\left( C \right):{x^2} + {y^2} + 4x + 4y - 17 = 0\] , biết tiếp tuyến vuông góc đường thẳng d: 3x – 4y – 2018 = 0 .
A. 3x – 4y + 39 = 0 hoặc 3x – 4y – 11 = 0;
B. 4x + 3y + 39 = 0 hoặc 3x – 4y – 11 = 0;
C. 3x – 4y + 39 = 0 hoặc 4x + 3y – 11 = 0;
D. 4x + 3y + 39 = 0 hoặc 4x + 3y – 11 = 0.
Xem lời giải »
Câu 1:
Phương trình nào là phương trình đường tròn có tâm I(–3; 4) và bán kính R = 2?
A. (x + 3)2 + (y – 4)2 – 4 = 0;
B. (x – 3)2 – (y – 4)2 = 4;
C. (x + 3)2 + (y + 4)2 = 4;
D. (x + 3)2 + (y – 4)2 = 2.
Xem lời giải »
Câu 2:
Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn khi và chỉ khi:
A. a2 + b2 ≥ c;
B. a2 + b2 < c;
C. a2 + b2 > c;
D. a2 + b2 ≤ c.
Xem lời giải »
Câu 3:
Cho phương trình đường tròn (C): x2 + y2 – 2ax – 2by + c = 0. Khi đó bán kính R được tính bởi công thức:
A. \(R = \sqrt {{a^2} + {b^2} + c} \);
B. \(R = \sqrt {{a^2} + {b^2} - c} \);
C. \(R = \sqrt {c - {a^2} - {b^2}} \);
D. R = a2 + b2 – c.
Xem lời giải »
Câu 4:
Tâm của đường tròn (C) có phương trình: (x – 2)2 + (y + 5)2 = 12 là:
A. D(2; 5);
B. E(5; 2);
C. F(2; –5);
D. G(–2; 5).
Xem lời giải »
Câu 5:
Phương trình nào sau đây là phương trình đường tròn?
A. (x – 1)2 + (y + 2)2 = 6;
B. (x + 5)2 + (y – 7)2 = 0;
C. (x – 2)2 + 2(y – 1)2 = 25;
D. (x + 3)2 – (y + 2)2 = 10.
Xem lời giải »
Câu 6:
Có bao nhiêu đường tròn đi qua ba điểm không thẳng hàng cho trước?
A. 0;
B. 1;
C. 2;
D. 3.
Xem lời giải »
Câu 7:
Phương trình nào sau đây là phương trình đường tròn?
A. x2 + y2 – 2xy – 1 = 0;
B. 2x2 + 2y2 – 2y = 0;
C. 3x2 + 3y2 – 3x + 3y + 12 = 0;
D. 6x2 + 5y2 + 2x + 3y – 1 = 0.
Xem lời giải »
Câu 1:
Với giá trị nào của m thì phương trình x2 + y2 – 2(m + 2)x + 4my + 19m – 6 = 0 là phương trình đường tròn?
A. 1 < m < 2;
B. –2 ≤ m ≤ 1;
C. m < 1 hoặc m > 2;
D. m < –2 hoặc m > 1.
Xem lời giải »
Câu 2:
Cho đường tròn (C): x2 + y2 + 2x + 4y – 20 = 0. Tìm mệnh đề sai trong các mệnh đề sau:
A. (C) có tâm I(1; 2);
B. (C) có đường kính 2R = 10;
C. (C) đi qua điểm M(2; 2);
D. (C) không đi qua điểm A(1; 1).
Xem lời giải »
Câu 3:
Đường tròn tâm I(1; 4) và đi qua điểm B(2; 6) có phương trình là:
A. (x + 1)2 + (y + 4)2 = 5;
B. \({\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} = \sqrt 5 \);
C. \({\left( {x + 1} \right)^2} + {\left( {y + 4} \right)^2} = \sqrt 5 \);
D. (x – 1)2 + (y – 4)2 = 5.
Xem lời giải »
Câu 4:
Một đường tròn có tâm I(3; –2), tiếp xúc với đường thẳng ∆: x – 5y + 1 = 0. Bán kính của đường tròn đó bằng:
A. 6;
B. \(\sqrt {26} \);
C. \(\frac{{14}}{{\sqrt {26} }}\);
D. \(\frac{7}{{13}}\).
Xem lời giải »
Câu 5:
Cho hai điểm A(1; 1) và B(7; 5). Phương trình đường tròn đường kính AB là:
A. x2 + y2 + 8x + 6y – 12 = 0;
B. x2 + y2 – 8x + 6y + 12 = 0;
C. x2 + y2 – 8x – 6y + 12 = 0;
D. x2 + y2 + 8x + 6y – 12 = 0.
Xem lời giải »
Câu 6:
Tâm của đường tròn đi qua ba điểm A(2; 1), B(2; 5), C(–2; 1) thuộc đường thẳng có phương trình:
A. x – y + 3 = 0;
B. x – y – 3 = 0;
C. x + 2y – 3 = 0;
D. x + y + 3 = 0.
Xem lời giải »
Câu 7:
Cho đường tròn (C): (x – 3)2 + (y – 1)2 = 10. Phương trình tiếp tuyến của (C) tại điểm A(4; 4) là:
A. x – 3y + 5 = 0;
B. x + 3y – 4 = 0;
C. x – 3y + 16 = 0;
D. x + 3y – 16 = 0.
Xem lời giải »
Câu 8:
Cho đường tròn (C): (x – 2)2 + (y – 2)2 = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:
A. x + y – 4 = 0 hoặc x – y – 2 = 0;
B. x = 5 hoặc y = –1;
C. 2x – y – 3 = 0 hoặc 3x + 2y – 2 = 0;
D. 3x – 2y – 2 = 0 hoặc 2x + 3y + 5 = 0.
Xem lời giải »
Câu 1:
Với giá trị nào của m thì đường thẳng ∆: 4x + 3y + m = 0 tiếp xúc với đường tròn (C): x2 + y2 – 9 = 0?
A. m = –3;
B. m = 3 hoặc m = –3;
C. m = 3;
D. m = 15 hoặc m = –15.
Xem lời giải »
Câu 2:
Cho đường tròn (C): x2 + y2 – 4x – 6y + 5 = 0. Đường thẳng d đi qua điểm A(3; 2) và cắt (C) theo một dây cung ngắn nhất có phương trình là:
A. 2x – y + 2 = 0;
B. x + y – 1 = 0;
C. x – y – 1 = 0;
D. x – y + 1 = 0.
Xem lời giải »
Câu 3:
Cho đường tròn (C): x2 + y2 + 2x – 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y – 15 = 0 là:
A. x + 2y = 0 hoặc x + 2y – 10 = 0;
B. x – 2y = 0 hoặc x + 2y + 10 = 0;
C. x + 2y – 1 = 0 hoặc x + 2y – 3 = 0;
D. x – 2y – 1 = 0 hoặc x – 2y – 3 = 0.
Xem lời giải »
Câu 4:
Đường tròn (C) đi qua hai điểm A(1; 3), B(3; 1) và có tâm nằm trên đường thẳng d: 2x – y + 7 = 0 có phương trình là:
A. (x – 7)2 + (y – 7)2 = 102;
B. (x + 7)2 + (y + 7)2 = 164;
C. (x – 3)2 + (y – 5)2 = 25;
D. (x + 3)2 + (y + 5)2 = 25.
Xem lời giải »
Câu 5:
Cho đường cong (Cm ): x2 + y2 + (m + 2)x – (m + 4)y + m + 1 = 0. Khi m thay đổi thì tâm của đường cong (Cm ) luôn nằm trên đường thẳng nào sau đây:
A. x + y + 1 = 0;
B. x + y – 1 = 0;
C. x + y – 2 = 0;
D. x – y + 2 = 0.
Xem lời giải »

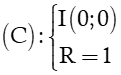 suy ra chỉ có phương trình x2 + y2 = 1 thoả mãn yêu cầu.
suy ra chỉ có phương trình x2 + y2 = 1 thoả mãn yêu cầu.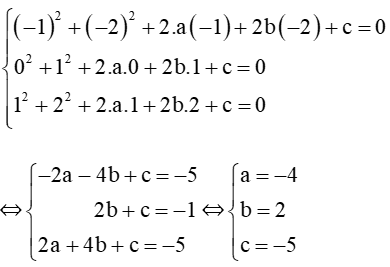
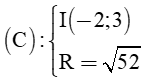 là: (x + 2)2 + (y – 3)2 = 52
là: (x + 2)2 + (y – 3)2 = 52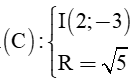 là:
là: