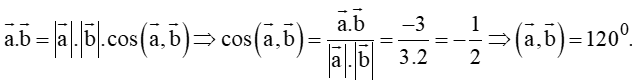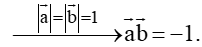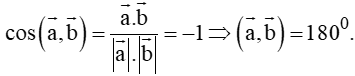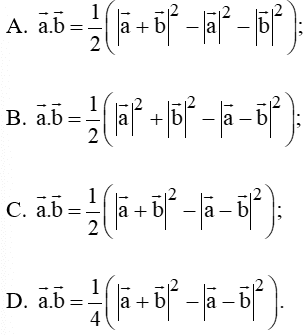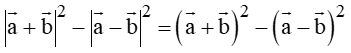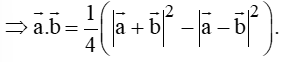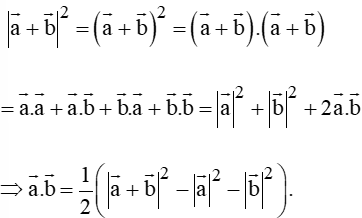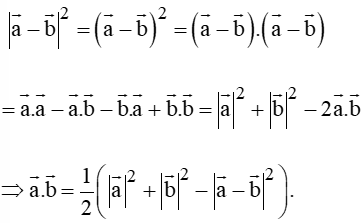15 Bài tập Tích vô hướng của hai vectơ (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Tích vô hướng của hai vectơ Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Tích vô hướng của hai vectơ (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Câu 1. Cho a → b → 0 →
A.
B. a → . b → = 0 ;
C. a → . b → = − 1
D.
Hiển thị đáp án
Đáp án đúng là: A
Ta có:
Do a → b → a → , b → = 0 0 ⇒ c o s a → , b → = 1
Vậy
Câu 2. Cho a → b → 0 → α a → b →
A. α = 180 0 ;
B. α = 0 0 ;
C. α = 90 0 ;
D. α = 45 0 .
Hiển thị đáp án
Đáp án đúng là: A
Ta có:
Mà theo giả thiết cos a → , b → = − 1 ⇒ a → , b → = 180 0 .
Câu 3. Cho hai vectơ a → b → α a → b →
A. α = 30 0 ;
B. α = 45 0 ;
C. α = 60 0 ;
D. α = 120 0 .
Hiển thị đáp án
Đáp án đúng là: D
Ta có:
Câu 4. Cho hai vectơ a → b → u → = 2 5 a → − 3 b → v → = a → + b → α a → b →
A. α = 90 0 ;
B. α = 180 0 ;
C. α = 60 0 ;
D. α = 45 0 .
Hiển thị đáp án
Đáp án đúng là: B
Ta có:u → ⊥ v → ⇒ u → . v → = 0 ⇔ 2 5 a → − 3 b → a → + b → = 0 ⇔ 2 5 a → 2 − 13 5 a → b → − 3 b → 2 = 0
Suy ra
Câu 5. Cho hai vectơ a → b →
Hiển thị đáp án
Đáp án đúng là: C
Nhận thấy C và D chỉ khác nhau về hệ số 1 2 1 4
Ta có:
= a → 2 + b → 2 + 2 a → . b → − a → 2 − b → 2 + 2 a → . b → = 4 a → . b →
- A đúng, vì:
- B đúng, vì
Câu 6. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng A B → . A C → .
A. A B → . A C → = 2 a 2 ;
B. A B → . A C → = − a 2 3 2 ;
C. A B → . A C → = − a 2 2 ;
D. A B → . A C → = a 2 2 .
Hiển thị đáp án
Đáp án đúng là: D
Xác định được góc A B → , A C → A ^ A B → , A C → = 60 0
Do đó A B → . A C → = A B . A C . c o s A B → , A C → = a . a . c o s 60 0 = a 2 2 .
Câu 7. Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng A B → . B C → .
A. A B → . B C → = a 2 ;
B. A B → . B C → = a 2 3 2 ;
C. A B → . B C → = − a 2 2 ;
D. A B → . B C → = a 2 2 .
Hiển thị đáp án
Đáp án đúng là: C
Xác định được góc A B → , B C → B ^ A B → , B C → = 120 0 B ^ = 60 ° o ).
Do đó A B → . B C → = A B . B C . c o s A B → , B C → = a . a . c o s 120 0 = − a 2 2 .
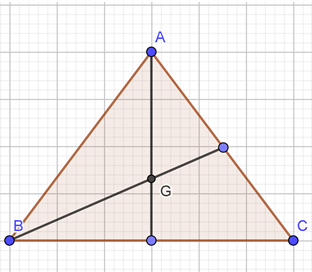
Câu 8. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
A. A B → . A C → = 1 2 a 2 ;
B. A C → . C B → = − 1 2 a 2 ;
C. G A → . G B → = a 2 6 ;
D. A B → . A G → = 1 2 a 2 .
Hiển thị đáp án
Đáp án đúng là: C
- Xác định được góc A B → , A C → A ^ A B → , A C → = 60 0 .
Do đó A B → . A C → = A B . A C . c o s A B → , A C → = a . a . c o s 60 0 = a 2 2 ⇒
- Xác định được góc A C → , C B → C ^ A C → , C B → = 120 0 .
Do đó A C → . C B → = A C . C B . c o s A C → , C B → = a . a . c o s 120 0 = − a 2 2 ⇒
- Xác định được góc G A → , G B → A G B ^ G A → , G B → = 120 0 .
Ta có: AG nằm trên đường trung tuyến cũng chính là đường cao của tam giác đều ABC, ta tính được đường cao, suy ra: AG = 2 3 3 2 a 3
Tương tự, GB = a 3
Do đó G A → . G B → = G A . G B . c o s G A → , G B → = a 3 . a 3 . c o s 120 0 = − a 2 6 ⇒
- Xác định được góc A B → , A G → G A B ^ A B → , A G → = 30 0 .
Do đó A B → . A G → = A B . A G . c o s A B → , A G → = a . a 3 . c o s 30 0 = a 2 2 ⇒
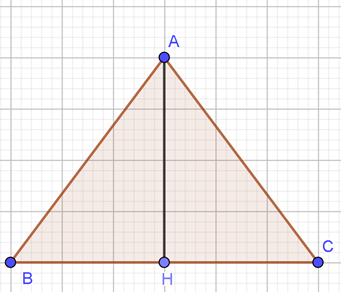
Câu 9. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH. Mệnh đề nào sau đây là sai?
A. A H → . B C → = 0 ;
B. A B → , H A → = 150 0 ;
C. A B → . A C → = a 2 2 ;
D. A C → . C B → = a 2 2 .
Hiển thị đáp án
Đáp án đúng là: D
Xác định được góc A C → , C B → A ^ A C → , C B → = 120 0 . o , do đó góc ngoài của góc A bằng 120o ).
Do đó A C → . C B → = A C . C B . c o s A C → , C B → = a . a . c o s 120 0 = − a 2 2 .
+) A đúng vì A H → ⊥ B C → A H → . B C → = 0 ;
+) B đúng vì AH chính là tia phân giác nên A B → , H A → = 150 0 ;
+) C đúng vì A B → . A C → = A B . A C . c o s A B → , A C → = a . a . c o s 60 0 = a 2 2 .
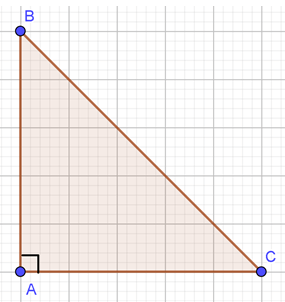
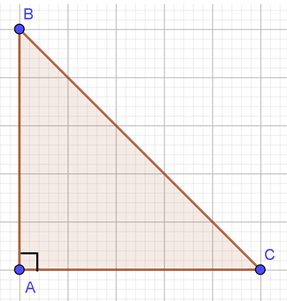
Câu 10. Cho tam giác ABC vuông cân tại A và có A B = A C = a . A B → . B C → .
A. A B → . B C → = − a 2 ;
B. A B → . B C → = a 2 ;
C. A B → . B C → = − a 2 2 2 ;
D. A B → . B C → = a 2 2 2 .
Hiển thị đáp án
Đáp án đúng là: A
Xác định được góc A B → , B C → B ^ A B → , B C → = 135 0 . A B C ^ 45 0
Độ dài BC là:B C 2 = A B 2 + A C 2 ⇔ B C = A B 2 + A C 2
⇔ B C = a 2
Do đó A B → . B C → = A B . B C . c o s A B → , B C → = a . a 2 . c o s 135 0 = − a 2 .
Câu 11. Cho tam giác ABC vuông cân tại Acó BC = 2. Tính tích vô hướng A B → . C A →
A.1;
B. 2;
C. 0;
D.3.
Hiển thị đáp án
Đáp án đúng là: C
Do tam giác ABC vuông cân tại A nên suy ra A B ⊥ C A ⇒ A B → . C A →
Câu 12. Cho tam giác ABC vuông tại A và có AB = c; AC = b. Tính B A → . B C → .
A.B A → . B C → = b 2 ;
B. B A → . B C → = c 2 ;
C. B A → . B C → = b 2 + c 2 ;
D.B A → . B C → = b 2 − c 2 .
Hiển thị đáp án
Đáp án đúng là: B
Áp dung định lý Py – ta – go ta có:
A B 2 + A C 2 = B C 2
⇔ B C = A B 2 + A C 2 = c 2 + b 2
Cos B = A B B C = c b 2 + c 2
Lại có: cos B chính là cos B A → ; B C →
Ta có:
B A → . B C → = B A . B C . c o s B A → , B C → = B A . B C . c o s B ^ = c . b 2 + c 2 . c b 2 + c 2 = c 2 .
Câu 13. Cho tam giác ABC có B C = a , C A = b , A B = c . P = A B → + A C → . B C → .
A. P = b 2 − c 2 ;
B. P = c 2 + b 2 2 ;
C. P = c 2 + b 2 + a 2 3 ;
D. P = c 2 + b 2 − a 2 2 .
Hiển thị đáp án
Đáp án đúng là: A
Ta có:P = A B → + A C → . B C → = A B → + A C → . B A → + A C → .
= A C → + A B → . A C → − A B → = A C → 2 − A B → 2 = A C 2 − A B 2 = b 2 − c 2 .
Câu 14. Cho tam giác ABC có B C = a , C A = b , A B = c . A M → . B C → .
A. A M → . B C → = b 2 − c 2 2 ;
B. A M → . B C → = c 2 + b 2 2 ;
C. A M → . B C → = c 2 + b 2 + a 2 3 ;
D. A M → . B C → = c 2 + b 2 − a 2 2 .
Hiển thị đáp án
Đáp án đúng là: A
Vì M là trung điểm của BC suy ra A B → + A C → = 2 A M → .
Khi đó A M → . B C → = 1 2 A B → + A C → . B C → = 1 2 A B → + A C → . B A → + A C →
= 1 2 A C → + A B → . A C → − A B → = 1 2 A C → 2 − A B → 2 = 1 2 A C 2 − A B 2 = b 2 − c 2 2 .
Câu 15. Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng O A → + O B → . A B → = 0
A. Tam giác OAB đều;
B. Tam giác OAB cân tại O;
C. Tam giác OAB vuông tại O;
D. Tam giác OAB vuông cân tại O.
Hiển thị đáp án
Đáp án đúng là: B
Ta có:O A → + O B → . A B → = 0 ⇔ O A → + O B → . O B → − O A → = 0
⇔ O B → 2 − O A → 2 = 0 ⇔ O B 2 − O A 2 = 0 ⇔ O B = O A .
Do đó, tam giác OAB cân tại O.
Câu 1:
Cho a → và b → là hai vectơ cùng hướng và đều khác vectơ 0 → . Mệnh đề nào sau đây đúng?
A. a → . b → = a → . b → ;
B. a → . b → = 0 ;
C. a → . b → = - 1
D. a → . b → = − a → . b →
Xem lời giải »
Câu 2:
Cho a → và b → khác vectơ 0 → . Xác định góc α giữa hai vectơ a → và b → khi a → . b → = − a → . b → .
A. α = 180 0 ;
B. α = 0 0 ;
C. α = 90 0 ;
D, α = 45 0 ;
Xem lời giải »
Câu 3:
Cho hai vectơ a → và b → thỏa mãn a → = 3 , b → = 2 và a → . b → = − 3. Xác định góc α giữa hai vectơ a → và b →
A. α = 30 0 ;
B. α = 45 0 ;
C. α = 60 0 ;
D. α = 120 0 ;
Xem lời giải »
Câu 4:
Cho hai vectơ a → và b → thỏa mãn a → = b → = 1 và hai vectơ u → = 2 5 a → − 3 b → và v → = a → + b → vuông góc với nhau. Xác định góc α giữa hai vectơ a → và b → .
A. α = 90 0 ;
B. α = 180 0 ;
C. α = 60 0 ;
D. α = 45 0 ;
Xem lời giải »
Câu 5:
Cho hai vectơ a → và b → . Đẳng thức nào sau đây sai?
A. a → . b → = 1 2 a → + b → 2 − a → 2 − b → 2 ;
B. a → . b → = 1 2 a → 2 + b → 2 − a → − b → 2 ;
C. a → . b → = 1 2 a → + b → 2 − a → − b → 2 ;
D. a → . b → = 1 4 a → + b → 2 − a → − b → 2 .
Xem lời giải »
Câu 6:
Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng A B → . A C → .
A. A B → . A C → = 2 a 2 ;
B. A B → . A C → = − a 2 3 2 ;
C. A B → . A C → = − a 2 2 ;
D. A B → . A C → = a 2 2 .
Xem lời giải »
Câu 7:
Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng A B → . B C → .
A. A B → . B C → = a 2 ;
B. A B → . B C → = a 2 3 2 ;
C. A B → . B C → = − a 2 2 ;
D. A B → . B C → = a 2 2 .
Xem lời giải »
Câu 8:
Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai?
A. A B → . A C → = 1 2 a 2 ;
B. A C → . C B → = − 1 2 a 2 ;
C. G A → . G B → = a 2 6 ;
D. A B → . A G → = 1 2 a 2 .
Xem lời giải »
Câu 9:
Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai?
A. A H → . B C → = 0 ;
B. A B → , H A → = 150 0 ;
C. A B → . A C → = a 2 2 ;
D. A C → . C B → = a 2 2 .
Xem lời giải »
Câu 10:
Cho tam giác ABC vuông cân tại A và có A B = A C = a . Tính A B → . B C → .
A. A B → . B C → = − a 2 ;
B. A B → . B C → = a 2 ;
C. A B → . B C → = − a 2 2 2 ;
D. A B → . B C → = a 2 2 2 ;
Xem lời giải »
Câu 11:
Cho tam giác ABC vuông cân tại A có BC = 2. Tính tích vô hướng A B → . C A →
A.1
B. 2
C. 0
D. 3
Xem lời giải »
Câu 12:
Cho tam giác ABC vuông tại A và có AB = c; AC = b. Tính B A → . B C → .
A. B A → . B C → = b 2 ;
B. B A → . B C → = a 2
C. B A → . B C → = b 2 + c 2 ;
D. B A → . B C → = b 2 − c 2 .
Xem lời giải »
Câu 13:
Cho tam giác ABC có B C = a , C A = b , A B = c . Tính P = A B → + A C → . B C → .
A. P = b 2 − c 2 ;
B. P = c 2 + b 2 2 ;
C. P = c 2 + b 2 + a 2 3 ;
D. P = c 2 + b 2 − a 2 2 .
Xem lời giải »
Câu 14:
Cho tam giác ABC có B C = a , C A = b , A B = c . Gọi M là trung điểm cạnh BC Tính A M → . B C → .
A. A M → . B C → = b 2 − c 2 2 ;
B. A M → . B C → = c 2 + b 2 2 ;
C. A M → . B C → = c 2 + b 2 + a 2 3 ;
D. A M → . B C → = c 2 + b 2 − a 2 2 .
Xem lời giải »
Câu 15:
Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng O A → + O B → . A B → = 0 là
A. T am giác OAB đều ;
B. T am giác OAB cân tại O;
C. T am giác OAB vuông tại O;
D. T am giác OAB vuông cân tại O.
Xem lời giải »
Câu 1:
Điền vào chỗ trống: “ Tích vô hướng của hai vectơ O A → O B → O A → O B →
A. O A → O B → O A → . O B → . cos ( O A → , O B → )
B. O A → O B → O A → . O B →
C. O A → O B → cos ( O A → , O B → )
D. O A → O B → A B →
Xem lời giải »
Câu 2:
Cho a → b → a → b → a → b → a → b →
A. 8;
B. 9;
C. 10;
D. 12.
Xem lời giải »
Câu 3:
Nếu a → b → 0 → a → b →
A. a → b →
B. a → b → a → b →
C. 0;
D. 0 →
Xem lời giải »
Câu 4:
Nếu hai vectơ a → b →
A. 1;
B. – 1;
C. 10;
D. 0.
Xem lời giải »
Câu 5:
Cho tam giác ABC vuông cân tại A có BC = 5 cm. Tính tích vô hướng A B → A C →
A. 1
B. 2
C. 0
D. 4
Xem lời giải »
Câu 6:
Cho a → b → a → b → a → b → a → b →
A. −18;
B. 18;
C. 9 ;
D. −9.
Xem lời giải »
Câu 7:
Cho a → b → a → b → a → b → a → b →
A. 28;
B. −28;
C. 14;
D. −14.
Xem lời giải »
Câu 1:
Cho hình vuông ABCD có cạnh bằng a. Khi đó tích vô hướng A C → . A D → bằng :
A. a2 ;
B. 2a2 ;
C. a2 3 ;
D. a2 2
Xem lời giải »
Câu 2:
Cho tam giác ABC đều có cạnh bằng a và đường cao AH. Khi đó tích vô hướng của A B → . A H → bằng ?
A. 3 a 2 4
B. 3 a 2 2
C. 2a2 ;
D. a2 .
Xem lời giải »
Câu 3:
Cho tam giác ABC vuông tại A có số đo góc B bằng 30° và AB = a . Khi đó tích vô hướng C A → C B →
A. 2a2 ;
B. a2 ;
C.a 2 2
D. a 2 3
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Giá trị của B A → . B C → bằng
A. 0;
B. c2 ;
C. a2 – b2 ;
D. a2 .
Xem lời giải »
Câu 5:
Cho tứ giác ABCD. Biểu thức A B → . C D → + B C → . C D → + C A → . C D → bằng
A. 0 →
B. CD2 ;
C. 0;
D. AB2 + AC2 + AD2 .
Xem lời giải »
Câu 6:
Cho hình thoi ABCD. Giá trị của A B → + A D → . B A → + B C →
A. 1;
B. 0;
C. AB2 – BC2 ;
D. AB2 + BC2 .
Xem lời giải »
Câu 7:
Nếu điểm M nằm trên đường trung trực của đoạn thẳng AB thìM A → + M B → . M A → − M B →
A. 1;
B. −AB2 ;
C. 0;
D. AB2 .
Xem lời giải »
Câu 8:
Cho ABC là tam giác đều. Mệnh đề nào sau đây đúng?
B. A B → . A C → = − A C → . A B →
C. A B → . A C → B C → = A B → A C → . B C →
D. A B → . A C → = B A → . B C →
Xem lời giải »
Câu 1:
Cho hai điểm B, C phân biệt. Tập hợp những điểm M thỏa mãn C M → . C B → = C M → 2
A. Đường tròn đường kính BC;
B. Đường tròn (B; BC);
C. Đường tròn (C; CB);
D. Một đường khác.
Xem lời giải »
Câu 2:
Cho tam giác ABC có H là trực tâm; A', B' lần lượt là chân đường cao xuất phát từ các điểm A, B. Gọi D, M, N, P lần lượt là trung điểm của AH, BC, CA, AB. Đẳng thức nào sau đây là đúng?
B. N M → . N D → = P D → . P C →
C. N M → . N D → = D P → . D M →
D. N M → . N D → = D A ' → . D B ' →
Xem lời giải »
Câu 3:
Cho ba điểm A, B, C phân biệt. Tập hợp những điểm M mà C M → . C B → = C A → . C B →
A. Đường tròn đường kính AB;
B. Đường thẳng đi qua A và vuông góc với BC;
C. Đường thẳng đi qua B và vuông góc với AC;
D. Đường thẳng đi qua C và vuông góc với AB.
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, có AB = 3, AC = 5. Vẽ đường cao AH. Tích vô hướng H B → . H C →
B. - 34
C. − 225 34
D. 225 34
Xem lời giải »
Câu 5:
Cho tam giác đều ABC cạnh a, với các đường cao AH, BK; vẽ HI ⊥ AC tại I.
Khẳng định nào sau đây đúng?
B. C B → . C A → = 4 C B → . C I →
C. A C → − A B → . B C → = B C → 2
D. Cả ba câu trên.
Xem lời giải »
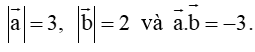

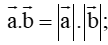
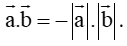
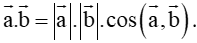
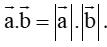
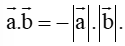
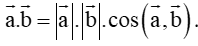
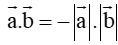 , suy ra
, suy ra