Bài 31 trang 109 Toán 11 Tập 2 - Kết nối tri thức

Giải Toán 11 Bài tập ôn tập cuối năm - Kết nối tri thức

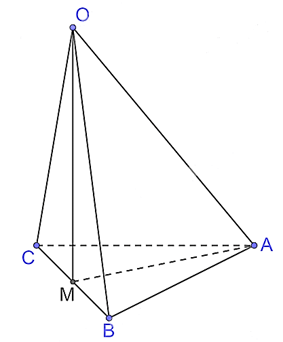
Bài 31 trang 109 Toán 11 Tập 2: Cho tứ diện OABC có OA = OB = OC = a, $\hat{A O B} = \hat{A O C} = 60 °$ và $\hat{B O C} = 90 °$ .

a) Chứng minh rằng (OBC) $⊥$ (ABC).

b) Tính theo a khoảng cách từ O đến mặt phẳng (ABC) và thể tích khối tứ diện OABC.

Lời giải:

Bài 31 trang 109 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Gọi M là trung điểm của BC.

Xét tam giác OBC có OB = OC = a nên tam giác OBC cân tại O mà OM là trung tuyến nên OM đồng thời là đường cao hay OM $⊥$ BC.

Vì tam giác OAC có OA = OC = a và $\hat{A O C} = 60 °$ nên tam giác OAC đều, suy ra AC = a.

Vì tam giác OAB có OA = OB = a và $\hat{A O B} = 60 °$ nên tam giác OAB đều, suy ra AB = a.

Xét tam giác OBC vuông tại O, có BC = $\sqrt{O C^{2} + O B^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .

Xét tam giác OBC vuông tại O, OM là đường cao, có

$\frac{1}{O M^{2}} = \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ $= \frac{1}{a^{2}} + \frac{1}{a^{2}} = \frac{2}{a^{2}}$ $\Rightarrow O M = \frac{a}{\sqrt{2}}$ .

Vì BC² = 2a² = a² + a² = AB² + AC² nên tam giác ABC vuông tại A.

Mặt khác AB = AC nên tam giác ABC cân tại A có AM là trung tuyến nên AM đồng thời là đường cao hay AM $⊥$ BC.

Xét tam giác ABC vuông tại A, AM là đường cao có:

$\frac{1}{A M^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$ $= \frac{1}{a^{2}} + \frac{1}{a^{2}} = \frac{2}{a^{2}}$ $\Rightarrow A M = \frac{a}{\sqrt{2}}$ .

Vì OA² = a² = $\frac{a^{2}}{2} + \frac{a^{2}}{2}$ = OM² + AM² nên tam giác OMA vuông tại M, suy ra OM ^ MA.

Vì OM $⊥$ MA và OM $⊥$ BC nên OM $⊥$ (ABC) mà OM $\subset$ (OBC), suy ra (OBC) $⊥$ (ABC).

b) Vì OM $⊥$ (ABC) nên d(O, (ABC)) = OM = $\frac{a}{\sqrt{2}}$ .

Có $S_{A B C} = \frac{1}{2} \cdot A B \cdot A C = \frac{a^{2}}{2}$ . Khi đó $V_{O A B C} = \frac{1}{3} \cdot S_{A B C} \cdot O M$ $= \frac{1}{3} \cdot \frac{a^{2}}{2} \cdot \frac{a}{\sqrt{2}} = \frac{a^{3} \sqrt{2}}{12}$ .

Vậy $V_{O A B C} = \frac{a^{3} \sqrt{2}}{12}$ .

Lời giải bài tập Toán 11 Bài tập ôn tập cuối năm hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán 11 Kết nối tri thức

Bài 31 trang 109 Toán 11 Tập 2 - Kết nối tri thức

Giải Toán 11 Bài tập ôn tập cuối năm - Kết nối tri thức

Xem thêm lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác: