Tính chất ba đường cao của tam giác (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 8: Tính chất ba đường cao của tam giác hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tính chất ba đường cao của tam giác (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Tính chất ba đường cao của tam giác

1. Đường cao của tam giác

Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chưa cạnh đối diện gọi là đường cao của tam giác đó.

Chú ý: Mỗi tam giác có ba đường cao.

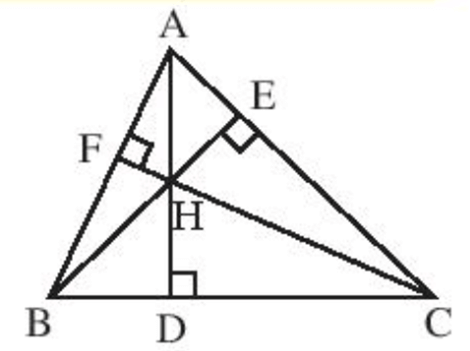
Ví dụ:Trong hình dưới đây, ba đoạn thẳng AD, BE, CF là ba đường cao của tam giác ABC. Hay còn nói ba đường thẳng AD, BE, CF là đường cao của tam giác ABC.

2. Tính chất ba đường cao của tam giác

Định lí: Ba đường cao của một tam giác cùng đi qua một điểm.

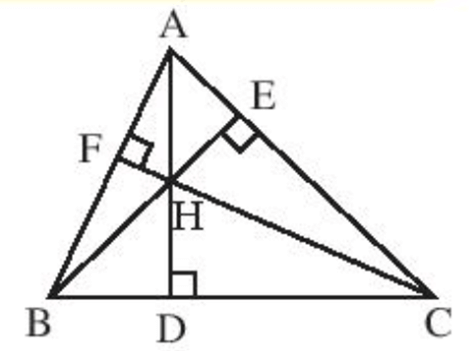
Ví dụ: Trong hình vẽ dưới đây ba đường cao AD, BE, CF của tam giác ABC cùng đi qua điểm H. Điểm H được gọi là trực tâm của tam giác ABC.

Chú ý:

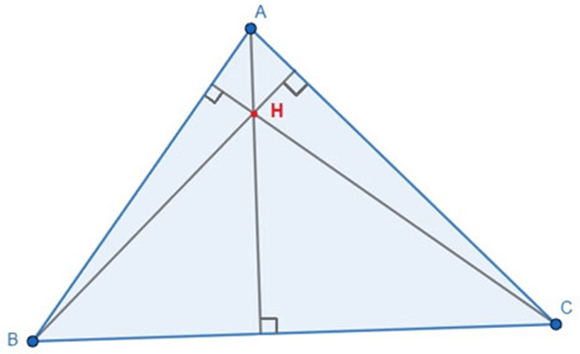
(1) Tam giác nhọn có trực tâm nằm bên trong tam giác (như hình vẽ dưới đây).

Tam giác ABC nhọn có trực tâm H nằm trong tam giác.

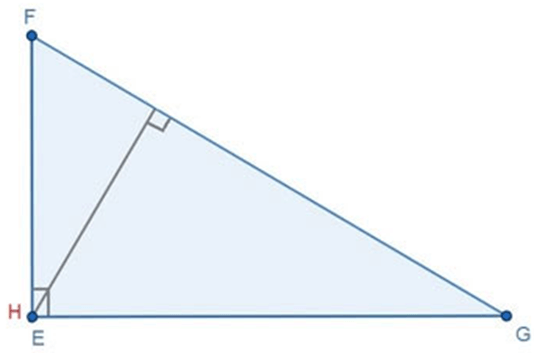
(2) Tam giác vuông có trực tâm trùng với đỉnh góc vuông (như hình vẽ dưới đây).

Tam giác EGF có trực tâm H trùng với đỉnh góc vuông E.

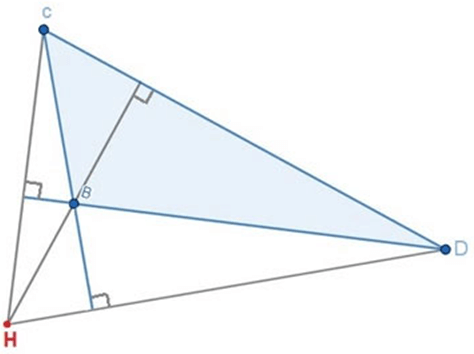
(3) Tam giác tù có trực tâm nằm ngoài tam giác (như hình vẽ dưới đây)

Tam giác tù BCD có tực tâm H nằm ngoài tam giác.

Bài tập Tính chất ba đường cao của tam giác

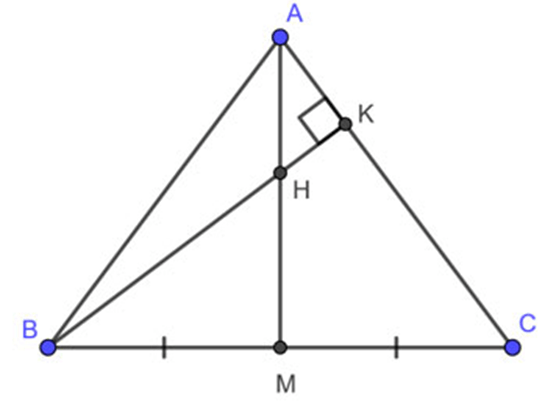
Bài 1: Cho tam giác ABC cân tại A, đường trung tuyến AM và đường cao BK. Gọi H là giao điểm của AM và BK. Chứng minh rằng CH vuông góc với AB.

Hướng dẫn giải

Vì tam giác ABC cân tại A nên đường trung tuyến AM cũng là đường cao của ABC.

Ta có H là giao điểm của hai đường cao AM và BK nên H là trực tâm của tam giác ABC

Suy ra CH là đường cao của tam giác ABC

Vậy CH vuông góc với AB.

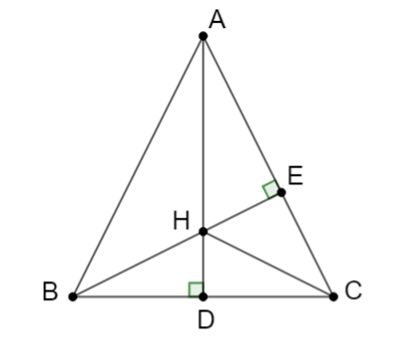
Bài 2: Cho tam giác ABC cân tại A có góc A nhọn và H là trực tâm. Cho biết $\overbrace{BHC}={150}^o.$ Tìm các góc của tam giác ABC.

Hướng dẫn giải

Tam giác ABC cân tại A có AD là đường cao đồng thời là đường trung trực.

Do đó điểm H thuộc đường trung trực của đoạn thẳng BC thì cách đều hai đầu mút B và C.

Vậy suy ra HB = HD. Từ đó ta có tam giác HBD cân tại H.

Suy ra $\overbrace{HBC}=\overbrace{HCB}$.

Ta có: $\overbrace{HBC}+\overbrace{HCB}+\overbrace{BHC}={180}^o$.

Suy ra $\overbrace{HBC}=\overbrace{HCB}=\frac{{180}^o-\overbrace{BHC}}{2}=\frac{{180}^o-{150}^o}{2}={15}^o$.

Xét ∆EBC vuông tại E có: $\overbrace{EBC}+\overbrace{ECB}={90}^o$.

Hay $\overbrace{ECB}=\overbrace{ACB}={90}^o-\overbrace{EBC}={90}^o-{15}^o={75}^o$.

Vậy suy ra $\overbrace{ABC}=\overbrace{ACB}={75}^o$.

Xét tam giác ABC có:

$\overbrace{BAC}={180}^o-\overbrace{ABC}-\overbrace{ACB}={180}^o-{75}^o-{75}^o={30}^o$.

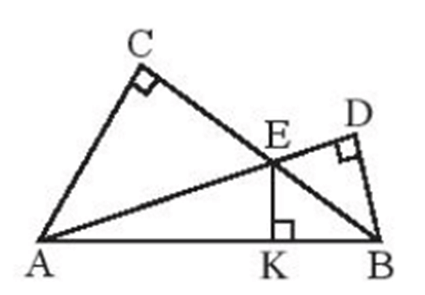
Bài 3: Cho hình vẽ dưới đây. Chứng minh AC, EK và BD cùng đi qua một điểm.

Hướng dẫn giải

Xét tam giác ABE có AC vuông góc với cạnh EB, EK vuông góc với cạnh AB và BD vuông góc với cạnh AE.

Nên suy ra ba đoạn thẳng AC, EK, BD là ba đường cao của tam giác AEB.

Vậy AC, EK, BD cùng đi qua một điểm và điểm đó chính là trực tâm của tam giác AEB.

Học tốt Tính chất ba đường cao của tam giác

Các bài học để học tốt Tính chất ba đường cao của tam giác Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 8: Tính chất ba đường cao của tam giác

• Giải sbt Toán 7 Bài 8: Tính chất ba đường cao của tam giác