Tập hợp các số hữu tỉ (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tập hợp các số hữu tỉ (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Tập hợp các số hữu tỉ

1. Số hữu tỉ

Số hữu tỉ là số được viết dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ, b ≠ 0. Các phân số bằng nhau biểu diễn cùng một số hữu tỉ.

Tập hợp các số hữu tỉ được kí hiệu là ℚ.

Ví dụ:

+ Các số $\frac{2}{5}$ ; $\frac{-3}{4}$; $\frac{7}{-8}$ là các số hữu tỉ.

+ Các số 5; −3,4; 3$\frac{2}{5}$ là các số hữu tỉ vì:

5 = $\frac{5}{1}$ = $\frac{10}{2}$ = …;

− 3,4 = $\frac{-34}{10}$ = $\frac{34}{10}$ = …;

3$\frac{2}{5}$ = $\frac{17}{5}$ = $\frac{34}{10}$ = …

Chú ý: Mỗi số nguyên là một số hữu tỉ.

2. Thứ tự trong tập hợp số hữu tỉ

- Với hai số hữu tỉ bất kì x, y ta luôn có: hoặc x = y hoặc x < y hoặc y > x.

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

Số hữu tỉ bé hơn 0 gọi là số hữu tỉ âm.

Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

Ví dụ: So sánh các cặp số hữu tỉ sau:

+ −0,8 và $\frac{-1}{5}$ .

Ta có −0,8 = $\frac{-8}{10}$; $\frac{-1}{5}$ = $\frac{-2}{10}$.

Vì −8 < −2 và 10 > 0 nên $\frac{-8}{10}$ < $\frac{-2}{10}$.

Vậy – 0,8 < $\frac{-1}{5}$.

+ −8$\frac{2}{3}$ và 0

Ta có −8$\frac{2}{3}$ = $\frac{-26}{3}$; 0 = $\frac{0}{3}$.

Vì − 5 < 0 và 3 > 0 nên $\frac{-26}{3}$ < $\frac{0}{3}$.

Vậy −8$\frac{2}{3}$ < 0.

Chú ý: Số hữu tỉ dương luôn luôn lớn hơn số hữu tỉ âm.

3. Biểu diễn số hữu tỉ trên trục số

- Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.

- Với hai số hữu tỉ bất kì x, y, nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ví dụ:

+ Để biểu diễn số hữu tỉ $\frac{3}{4}$ ta làm như sau:

– Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn thẳng mới bằng $\frac{1}{4}$ đơn vị cũ.

– Số hữu tỉ $\frac{3}{4}$ được biểu diễn bởi điểm A nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới trong hình dưới.

+ Để biểu diễn số hữu tỉ $\frac{3}{-2}$ trên trục số ta làm như sau:

– Viết $\frac{3}{-2}$ dưới dạng phân số với mẫu số dương $\frac{3}{-2}$ = $\frac{-3}{2}$.

– Chia đoạn thẳng đơn vị thành hai phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ.

– Số hữu tỉ $\frac{3}{-2}$ được biểu diễn bởi điểm B nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới như hình dưới.

+ Ta có $\frac{-5}{2}$ < − 2 nên trên trục số nằm ngang điểm $\frac{-5}{2}$ nằm bên trái điểm −2 như hình dưới.

4. Số đối của một số hữu tỉ

Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.

Số đối của số hữu tỉ x kí hiệu là −x.

Ví dụ:

$\frac{-4}{3}$ là số đối của $\frac{4}{3}$; $\frac{4}{3}$ là số đối của $\frac{-4}{3}$.

0, 25 là số đối của −0,25; −0,25 là số đối của 0,25.

Số đối của $1\frac{1}{2}$ là $\frac{-3}{2}$ và ta viết là $-1\frac{1}{2}$.

Chú ý:

Mọi số hữu tỉ đều có một số đối.

Số đối của số 0 là số 0.

Với hai số hữu tỉ âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

Bài tập Tập hợp các số hữu tỉ

Bài 1. Thay bằng kí hiệu ∈, ∉ thích hợp.

−7 ℕ ; −17 (ảnh -2) ℤ ; −38 ℚ ;

$\frac{4}{5}$ ℤ ; $\frac{4}{5}$ ℚ ; 0,25 ℤ ; 3,25 $\mathbb{Q}$ .

Hướng dẫn giải

Ta có – 7 là số nguyên âm nên –7 không thuộc ℕ. Do đó ta viết .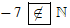

Ta có −17 là số nguyên âm nên −17 thuộc ℤ. Do đó ta viết

Ta có – 38 là số nguyên âm nên –38 thuộc ℚ. Do đó ta viết .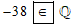

Ta có $\frac{4}{5}$ là số hữu tỉ nên $\frac{4}{5}$ không thuộc ℤ. Do đó ta viết .

Ta có $\frac{4}{5}$ là số hữu tỉ nên $\frac{4}{5}$ thuộc ℚ. Do đó ta viết .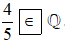

Ta có 0,25 là số hữu tỉ nên 0,25 không thuộc ℤ. Do đó ta viết .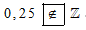

Ta có 3,25 là số hữu tỉ nên 3,25 thuộc ℚ. Do đó ta viết .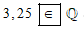

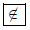
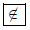
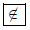
−7 ℕ; −17 ℤ; −38 ℚ;

$\frac{4}{5}$ ℤ; $\frac{4}{5}$ ℚ; 0,25 ℤ; 3,25 ℚ.

Bài 2.

a) Trong các phân số sau, phân số nào biểu diễn số hữu tỉ $\frac{-5}{9}$ ?

$\frac{-10}{18}$; $\frac{10}{18}$; $\frac{15}{-27}$; $-\frac{20}{36}$; $\frac{-25}{27}$.

b) Tìm số đối của mỗi số sau: 12; $\frac{4}{9}$ ; −0, 375; $\frac{0}{5}$; $-2\frac{2}{5}$.

Hướng dẫn giải

a) Ta có: $\frac{-10}{18}=\frac{-10:2}{18:2}=\frac{-5}{9}$ ;

$\frac{10}{18}=\frac{10:2}{18:2}=\frac{5}{9}$;

$\frac{15}{-27}=\frac{15:3}{-27:3}=\frac{5}{-9}=\frac{-5}{9}$;

$-\frac{20}{36}=-\frac{20:4}{36:4}=-\frac{5}{9}=\frac{-5}{9}$;

Vậy các phân số biểu diễn số hữu tỉ $\frac{-5}{9}$ là: $\frac{-10}{18}$; $\frac{15}{-27}$; $-\frac{20}{36}$.

b)

Số đối của 12 là −12.

Số đối của $\frac{4}{9}$là $\frac{-4}{9}$.

Số đối của −0,375 là – (−0,375) = 0,375.

Số đối của $\frac{0}{5}$ là $\frac{-0}{5}$.

Số đối của $-2\frac{2}{5}$ là $\frac{12}{5}$ và ta viết là $2\frac{2}{5}$.

Bài 3.

a) Các điểm A, B, C trong hình dưới biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ $\frac{-2}{5}$; $1\frac{1}{5}$; $\frac{3}{5}$; − 0,8 trên trục số.

Hướng dẫn giải

a) Dựa vào hình vẽ, ta thấy đoạn thẳng đơn vị cũ được chia thành 5 đoạn bằng nhau.

Ta được đoạn thẳng đơn vị mới bằng $\frac{1}{4}$ đoạn thẳng đơn vị cũ.

Điểm A nằm về bên trái gốc O và cách gốc O một đoạn bằng 7 đơn vị mới.

Khi đó, điểm A biểu diễn cho số hữu tỉ $-\frac{7}{4}$.

Điểm B nằm về bên phải gốc O và cách gốc O một đoạn bằng 3 đơn vị mới.

Khi đó, điểm B biểu diễn cho số hữu tỉ $\frac{3}{4}$.

Điểm C nằm về bên phải gốc O và cách gốc O một đoạn bằng 5 đơn vị mới.

Khi đó, điểm C biểu diễn cho số hữu tỉ $\frac{5}{4}$.

b) Ta có $1\frac{1}{5}=\frac{6}{5}$ ; − 0,8 = $-\frac{8}{10}=\frac{-4}{5}$.

Chia đoạn thẳng đơn vị cũ thành 5 đoạn bằng nhau ta được đoạn thẳng đơn vị mới bằng $\frac{1}{5}$ đoạn đơn vị cũ. Khi đó:

Điểm M là điểm biểu diễn cho số hữu tỉ $-\frac{2}{5}$ nên điểm M nằm về bên trái gốc O và cách gốc O một đoạn bằng 2 đơn vị mới.

Điểm N biểu diễn cho số hữu tỉ $1\frac{1}{5}$ nên điểm N nằm về bên phải gốc O và cách gốc O một đoạn bằng 6 đơn vị mới.

Điểm P biểu diễn cho số hữu tỉ $\frac{3}{5}$ nên điểm P nằm về bên phải gốc O và cách gốc O một đoạn bằng 3 đơn vị mới.

Điểm Q biểu diễn cho số hữu tỉ –0,8 nên điểm Q nằm về bên phải gốc O và cách gốc O một đoạn bằng 4 đơn vị mới.

Do đó ta có hình vẽ:

Bài 4.

a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

$\frac{5}{12}$; $\frac{-4}{5}$; $2\frac{2}{3}$; −2; $\frac{0}{234}$; −0,32.

b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.

Hướng dẫn giải

a)Số hữu tỉ dương là: $\frac{5}{12}$; $2\frac{2}{3}$.

Số hữu tỉ âm là: $\frac{-4}{5}$; −2; −0,32.

Số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: $\frac{0}{234}$.

b) Ta chia dãy số thành các nhóm sau:

Nhóm 1 là nhóm các số hữu tỉ âm: $\frac{-4}{5}$; −2; −0,32.

Ta có: $\frac{-4}{5}=\frac{-20}{25}$; −2 = $\frac{-2}{1}=\frac{-10}{5}=\frac{-50}{25}$;

−0,32 = $\frac{-32}{100}=-\frac{8}{25}$.

Vì –50 < –20 < –8 nên $\frac{-50}{25}<\frac{-20}{25}<-\frac{8}{25}$.

Hay −2 < $\frac{-4}{5}$ < −0,32.

Nhóm 2 là nhóm các số hữu tỉ dương: $\frac{5}{12}$; $2\frac{2}{3}$.

Ta có: $\frac{5}{12}$; $2\frac{2}{3}=\frac{8}{3}=\frac{32}{12}$.

Vì 5 < 32 nên $\frac{5}{12}$ < $\frac{32}{12}$ hay $\frac{5}{12}$ < $2\frac{2}{3}$.

Nhóm 3 gồm số $\frac{0}{234}$.

Vì số hữu tỉ âm nhỏ hơn số 0 và nhỏ hơn số hữu tỉ dương nên ta có:

−2 < $\frac{-4}{5}$ < −0,32 < $\frac{0}{234}$ < $\frac{5}{12}$ < $2\frac{2}{3}$.

Vậy theo thứ tự từ bé đến lớn ta có dãy số sau:−2; $\frac{-4}{5}$; −0,32; $\frac{0}{234}$; $\frac{5}{12}$; $2\frac{2}{3}$.

Bài 5. So sánh các cặp số hữu tỉ sau:

a) $\frac{2}{-5}$ và $\frac{-3}{8}$;

b) −0,85 và $\frac{-17}{20}$;

c) $\frac{-137}{200}$ và $\frac{37}{-25}$;

d) $-1\frac{3}{10}$ và $-\left(\frac{-10}{-13}\right)$.

Hướng dẫn giải

a) Ta có $\frac{2}{-5}=\frac{-16}{40}$; $\frac{-3}{8}=\frac{-15}{40}$.

Vì −16 < −15 và 40 > 0 nên $\frac{-16}{40}$ < $\frac{-15}{40}$.

Vậy $\frac{2}{-5}$ < $\frac{-3}{8}$.

b) Ta có $-0,85=\frac{-85}{100}=\frac{-17}{20}$

nên −0,85 = $\frac{-17}{20}$.

Vậy −0,85 = $\frac{-17}{20}$.

c) Ta có $\frac{37}{-25}=\frac{-296}{200}$.

Vì −137 > −296 và 200 > 0 nên $\frac{-137}{200}$> $\frac{-296}{200}$.

Vậy $\frac{-137}{200}$ > $\frac{37}{-25}$.

d) Ta có $-1\frac{3}{10}=\frac{-13}{10}=\frac{-169}{130}$;

$-\left(\frac{-10}{-13}\right)=\frac{-10}{13}=\frac{-100}{130}$.

Vì −169 < −100 và 130 > 0 nên $\frac{-169}{130}$< $\frac{-100}{130}$.

Vậy $-1\frac{3}{10}$ < $-\left(\frac{-10}{-13}\right)$.

Bài 6. So sánh các cặp số hữu tỉ sau:

a) $\frac{-2}{3}$ và $\frac{1}{200}$;

b) $\frac{139}{138}$ và $\frac{1375}{1376}$;

c) $\frac{-11}{33}$ và $\frac{25}{-76}$.

Hướng dẫn giải

a) Ta có $\frac{-2}{3}$ < 0; $\frac{1}{200}$> 0 nên $\frac{-2}{3}$< $\frac{1}{200}$.

Vậy $\frac{-2}{3}$< $\frac{1}{200}$.

b) Ta có $\frac{139}{138}>\frac{138}{138}=1$; $\frac{1375}{1376}<\frac{1376}{1376}=1$.

Do đó $\frac{139}{138}$ > $\frac{1375}{1376}$.

Vậy $\frac{139}{138}$ > $\frac{1375}{1376}$.

c) Ta có: $\frac{-11}{33}=\frac{-1}{3}=\frac{25}{-75}$.

Vì −75 > −76 và 25 > 0 nên $\frac{25}{-75}$< $\frac{25}{-76}$.

Vậy $\frac{-11}{33}$< $\frac{25}{-76}$.

Bài 7. Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.

a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto Rico. Giải thích.

b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên. Giải thích.

Hướng dẫn giải

a) Độ cao của rãnh Puerto Rico là: – 8,6 m.

Vì 7,7 < 8,0 < 8,6 nên −7,7 > −8,0 > −8,6

Do đó những rãnh đại dương có độ cao cao hơn rãnh Puerto Rico là: Rãnh Romanche; Rãnh Peru – Chile.

Vậy những rãnh đại dương có độ cao cao hơn rãnh Puerto Rico là: Rãnh Romanche; Rãnh Peru – Chile.

b) Vì 7,7 < 8,0 < 8,6 < 10,5 nên −7,7 > −8,0 > −8,6 > –10,5

Do đó rãnh đại dương có độ cao thấp nhất trong bốn rãnh trên là: Rãnh Philippine.

Vậy rãnh đại dương có độ cao thấp nhất trong bốn rãnh trên là: Rãnh Philippine.

Học tốt Tập hợp các số hữu tỉ

Các bài học để học tốt Tập hợp các số hữu tỉ Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 1: Tập hợp các số hữu tỉ

• Giải sbt Toán 7 Bài 1: Tập hợp các số hữu tỉ