Tổng hợp lý thuyết Toán 7 Chương 8 Chân trời sáng tạo

---

Với tổng hợp lý thuyết Toán 7 Chương 8: Tam giác hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tổng hợp lý thuyết Toán 7 Chương 8 Chân trời sáng tạo

Lý thuyết tổng hợp Toán 7 Chương 8

1. Tổng số đo ba góc của một tam giác:

* Định lí: Tổng số đo của ba góc của một tam giác bằng 180°.

* Chú ý:

- Tam giác có 3 góc nhọn được gọi là tam giác nhọn.

- Tam giác có một góc vuông được gọi là tam giác vuông, cạnh đối diện góc vuông gọi là cạnh huyền, hai cạnh còn lại gọi là hai cạnh góc vuông.

- Tam giác có một góc tù được gọi là tam giác tù.

* Nhận xét: Trong một tam giác vuông, tổng hai góc nhọn bằng 90°

2. Quan hệ giữa ba cạnh của một tam giác:

* Định lí: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn hai cạnh còn lại.

* Nhận xét: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại.

* Lưu ý: Khi xét độ dài ba đoạn thẳng có thỏa mãn các bất đẳng thức tam giác hay không, ta chỉ cần so sánh độ dài lớn nhát với tổng của hai độ dài còn lại, hoặc so sánh độ dài nhỏ nhất với hiệu của hai độ dài còn lại.

3. Định nghĩa hai tam giác bằng nhau:

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

* Chú ý:

- Khi vẽ hai tam giác bằng nhau, các cạnh hoặc các góc bằng nhau được đánh dấu bởi những kí hiệu giống nhau.

- Khi dùng kí hiệu hai tam giác bằng nhau, ta phải viết các đỉnh tương ứng theo cùng thứ tự.

4. Các trường hợp bằng nhau của hai tam giác

* Trường hợp bằng nhau thứ nhất: cạnh – cạnh – cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

*Trường hợp bằng nhau thứ hai: cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

* Trường hợp bằng nhau thứ ba: góc – cạnh – góc (g.c.g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

5. Các trường hợp bằng nhau của hai tam giác vuông

* Trường hợp hai cạnh góc vuông:

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp c.g.c).

* Trường hợp một cạnh góc vuông và một góc nhọn:

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp g.c.g).

* Trường hợp cạnh huyền và một cạnh góc vuông:

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

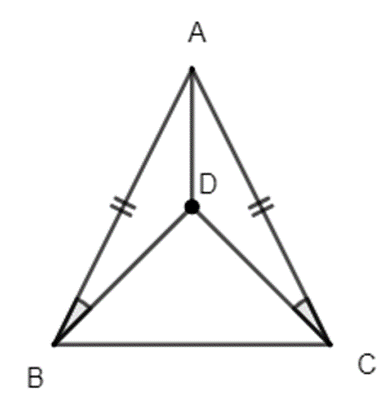
6. Định nghĩa tam giác cân:

Tam giác cân là tam giác có hai cạnh bằng nhau.

7. Tính chất của tam giác cân:

Định lí 1: Trong một tam giác cân, hai góc ở đáy bằng nhau.

Định lí 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

* Chú ý:

- Tam giác đều là tam giác có ba cạnh bằng nhau.

- Tam giác vuông cân là tam giác vuông và cân.

* Nhận xét:

- Tam giác cân có một góc 60° là tam giác đều.

- Tam giác cân có một góc ở đáy bằng 45° là tam giác vuông cân.

8. Quan hệ giữa cạnh và góc trong một tam giác:

Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại, đối diện với cạnh lớn hơn là góc lớn hơn.

Cho ∆ABC có: CA > AB suy ra $\overbrace{B}>\overbrace{C}$.

Cho ∆DGE có : $\overbrace{D}>\overbrace{E}$ suy ra GE > GD.

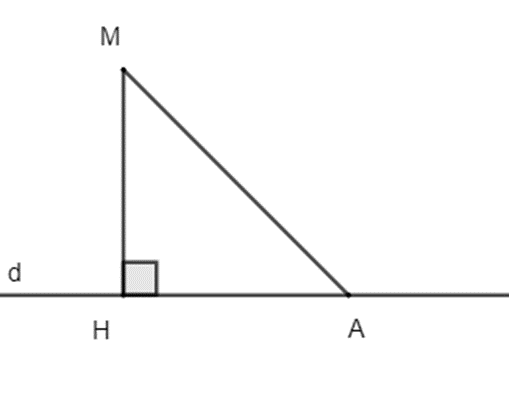
9. Đường vuông góc và đường xiên:

- Đoạn thẳng MH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm M đến đường thẳng d.

- Đoạn thẳng MA gọi là một đường xiên kẻ từ M đến đường thẳng d.

- Độ dài đoạn MH được gọi là khoảng cách từ điểm M đến đường thẳng d.

10. Mối quan hệ giữa đường vuông góc và đường xiên:

Trong số các đường thẳng nối từ một điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.

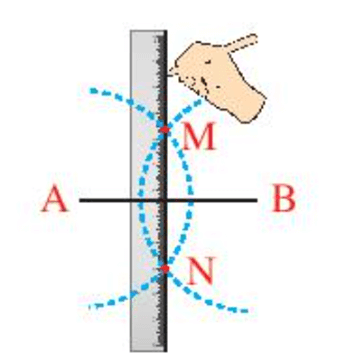
11. Đường trung trực của một đoạn thẳng

Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đó.

12. Tính chất của đường trung trực

Định lí 1: Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Định lí 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Chú ý: Các bước dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa:

(1) Khi vẽ hai cung tròn trên, ta phải lấy bán kính lớn hơn $\frac{1}{2}$AB thì hai cung tròn đó mới có hai điểm chung.

Ví dụ:

+ Lấy A làm tâm vẽ cung tròn bán kính lớn hơn $\frac{1}{2}$AB (như hình vẽ dưới đây)

+ Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (như hình vẽ dưới đây)

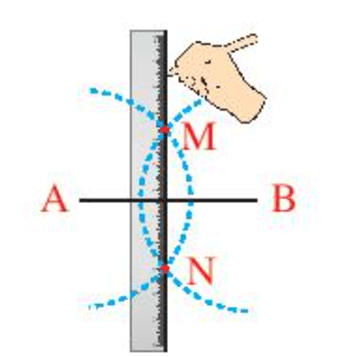
+ Hai cung tròn này cắt nhau tại M và N (như hình vẽ dưới đây). Dùng thức vẽ đường thẳng MN. Khi đó MN là đường trung trực đoạn thẳng AB.

Chứng minh:

Hai cung tròn có cùng bán kính và cắt nhau tại M và N nên ta suy ra được MA = MB = NA = NB.

Khi đó, M và N là hai điểm cách đều hai đầu mút A và B của đoạn thẳng AB nên suy M, N nằm trên đường trung trực của đoạn thẳng AB (Theo định lí 2).

Vậy suy ra MN là đường thẳng trung trực của đoạn thẳng AB.

(2) Giao điểm của đường thẳng MN với đoạn thẳng AB là trung điểm của đoạn thẳng AB nên cách vẽ trên cũng là cách dựng trung điểm của đoạn thẳng bằng thước và compa.

Chứng minh: Từ chú ý trên ta chứng minh được MN là đường trung trực của đoạn thẳng AB khi đó MN vuông góc với AB tại trung điểm của AB. Nên suy ra MN giao với AB tại trung điểm của đoạn thẳng AB.

13. Đường trung trực của tam giác

Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.

Chú ý: Mỗi tam giác có ba đường trung trực.

14. Tính chất ba đường trung trực của tam giác

Định lí: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

15. Đường trung tuyến của tam giác

Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm cạnh đối diện.

Chú ý: mỗi tam giác có ba đường trung tuyến.

16. Tính chất ba đường trung tuyến của tam giác

Định lí: Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

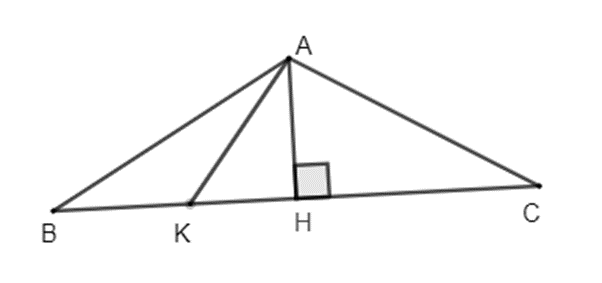
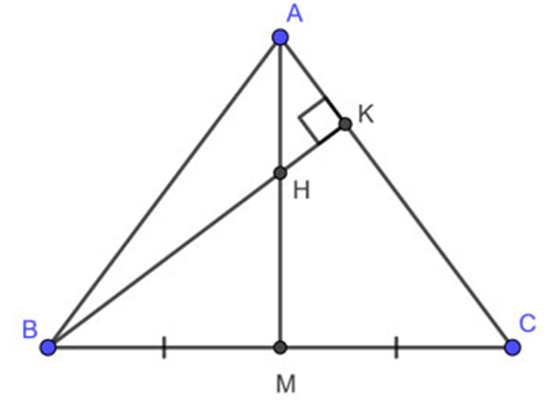
17. Đường cao của tam giác

Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chưa cạnh đối diện gọi là đường cao của tam giác đó.

Chú ý: Mỗi tam giác có ba đường cao.

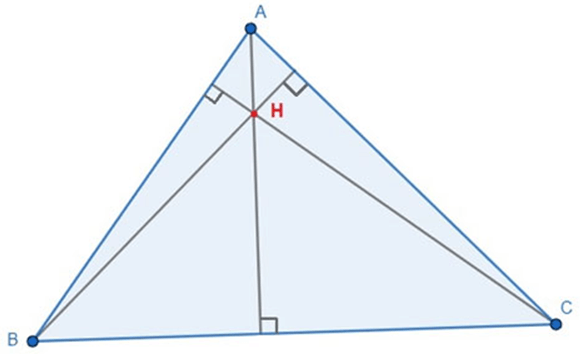
18. Tính chất ba đường cao của tam giác

Định lí: Ba đường cao của một tam giác cùng đi qua một điểm.

Chú ý:

(1) Tam giác nhọn có trực tâm nằm bên trong tam giác (như hình vẽ dưới đây).

Tam giác ABC nhọn có trực tâm H nằm trong tam giác.

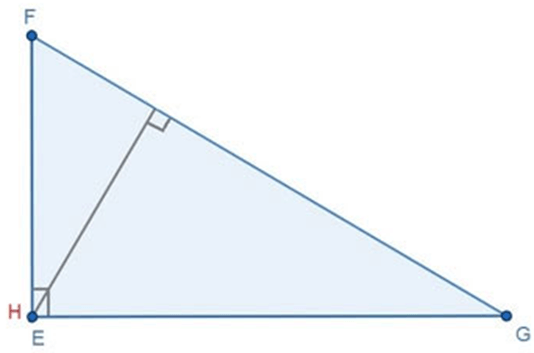
(2) Tam giác vuông có trực tâm trùng với đỉnh góc vuông (như hình vẽ dưới đây).

Tam giác EGF có trực tâm H trùng với đỉnh góc vuông E.

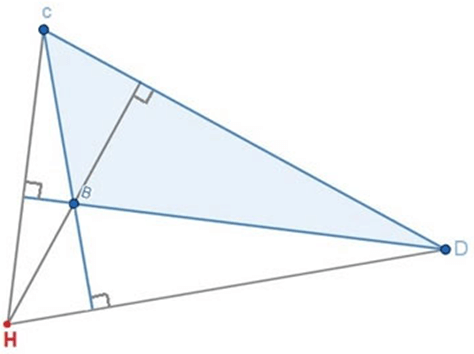
(3) Tam giác tù có trực tâm nằm ngoài tam giác (như hình vẽ dưới đây)

Tam giác tù BCD có tực tâm H nằm ngoài tam giác.

19. Đường phân giác của tam giác

Cho tam giác ABC, tia phân giác góc A cắt cạnh BC tại D. Khi đó đoạn thẳng AD được gọi là đường phân giác góc A của tam giác ABC.

Chú ý: Mỗi tam giác có ba đường phân giác.

20. Tính chất ba đường phân giác của tam giác

Định lí: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác.

Bài tập tổng hợp Toán 7 Chương 8

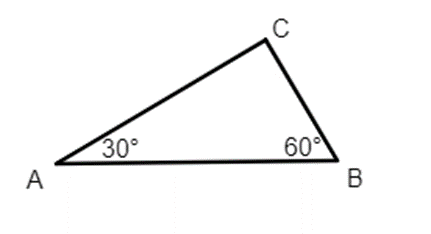
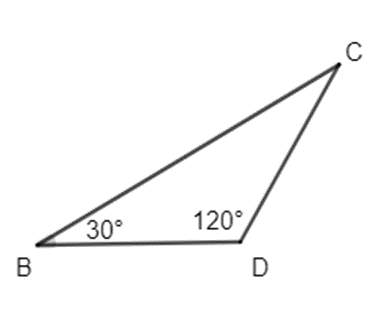
Bài 1: Tìm số đo các góc chưa biết của các tam giác sau:

a)

b)

Hướng dẫn giải:

a) Xét tam giác ABC, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{A}+\overbrace{B}+\overbrace{C}={180}^o$

Suy ra $\overbrace{C}={180}^o-\overbrace{A}-\overbrace{B}$

= 180° − 30° − 60° = 90°.

Vậy $\overbrace{C}={90}^o$.

b) Xét tam giác BCD, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{B}+\overbrace{C}+\overbrace{D}={180}^o$

Suy ra $\overbrace{C}={180}^o-\overbrace{B}-\overbrace{D}$

= 180° − 30° − 120° = 30°

Vậy $\overbrace{C}={30}^o$.

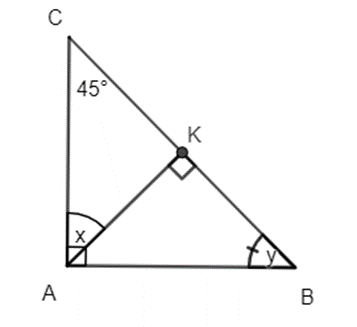
Bài 2: Tính tổng số đo của các góc x và y trong hình sau:

Hướng dẫn giải:

Xét tam giác ABC, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{A}+\overbrace{B}+\overbrace{C}={180}^o$

Suy ra $\overbrace{B}={180}^o-\overbrace{A}-\overbrace{C}$

= 180° − 90° − 45° = 45° = y

Tương tự xét tam giác AKC, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{A}+\overbrace{K}+\overbrace{C}={180}^o$

Suy ra $\overbrace{A}={180}^o-\overbrace{C}-\overbrace{K}$

= 180° − 90° − 45° = 45° = x

Vậy x + y = 45° + 45° = 90°.

Bài 3: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 6 cm, 8 cm, 10 cm;

b) 3 cm, 2 cm, 6 cm;

c) 3 cm, 2 cm, 5 cm.

Hướng dẫn giải:

a) Ta thấy: 10 < 6 + 8 = 12

Suy ra bộ ba độ dài đoạn thẳng 6 cm, 8 cm, 10 cm có thể là bộ ba độ dài cạnh của một tam giác.

b) Ta thấy: 6 > 2 + 3 = 5

Suy ra bộ ba độ dài đoạn thẳng 3 cm, 2 cm, 6 cm không thể là bộ ba độ dài cạnh của một tam giác.

c) Ta thấy: 5 = 3 + 2

Suy ra bộ ba độ dài đoạn thẳng 3 cm, 2 cm, 5 cm không thể là bộ ba độ dài cạnh của một tam giác.

Vậy trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba 6 cm, 8 cm, 10 cm có thể là độ dài ba cạnh của một tam giác.

Bài 4: Cho tam giác HIK có HK = 4 cm, HI = 1 cm. Tìm độ dài của cạnh IK, biết rằng độ dài này là một số nguyên.

Hướng dẫn giải:

Dựa vào quan hệ của các cạnh trong một tam giác ta có:

HK – HI < IK < HK + HI

Suy ra 4 – 1 < IK < 4 + 1

3 < IK < 5

Vì độ dài IK là một sô nguyên nên suy ra IK = 4 cm.

Vậy độ dài của IK = 4 cm.

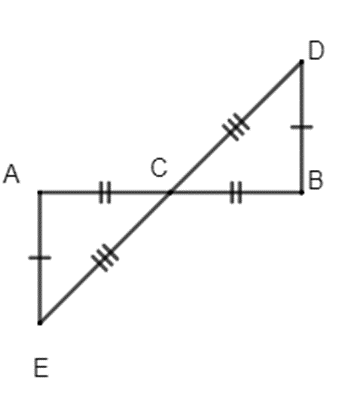
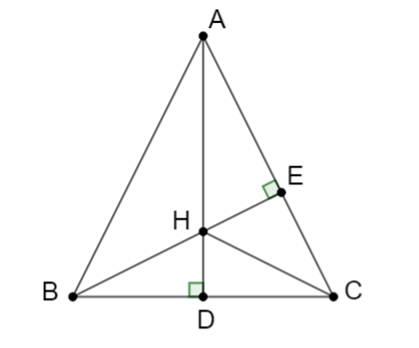
Bài 5. Quan sát hình sau và điền vào chỗ trống:

a) ∆ACE = …;

b) ∆EAC = …;

c) ∆CAE = ….

Hướng dẫn giải:

Theo hình vẽ trên ta có:

AC = BC; CD = CE; AE = BD.

Do đó: ∆ACE = ∆BCD (c.c.c);∆EAC = ∆DBC (c.c.c);∆CAE = ∆CBD (c.c.c).

Vậy ta điền vào như sau:

a) ∆ACE = ∆BCD;

b) ∆EAC = ∆DBC;

c) ∆CAE = ∆CBD.

Bài 6. Cho ∆FCG = ∆MNQ và $\overbrace{G}={30}^o$, CG = 4 cm, MN = 3 cm. Tính số đo $\overbrace{Q}$ và độ dài NQ, FC.

Hướng dẫn giải:

Theo bài cho ta có ∆FCG = ∆MNQ.

Suy ra ta có: $\overbrace{G}=\overbrace{Q}={30}^o$;

CG = NQ = 4 cm;

FC = MN = 3 cm.

Vậy $\overbrace{Q}={30}^o$; NQ = 4 cm; MN = 3 cm.

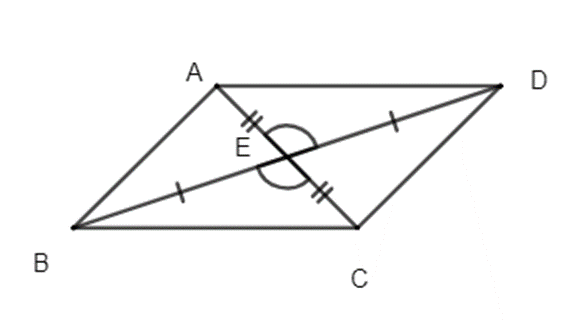
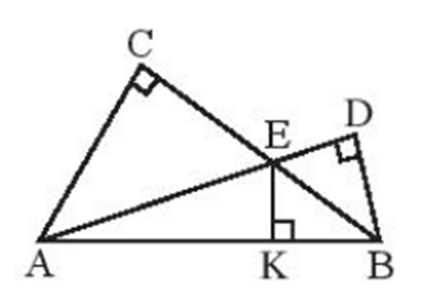
Bài 7. Cho hình sau:

Chứng minh rằng:

a) ∆AED = ∆CEB;

b) AD // BC.

Hướng dẫn giải:

a) Xét ∆AED và ∆CEB có:

AE = CE (gt);

$\overbrace{AED}=\overbrace{CEB}$ (gt);

BE = DE (gt)

Do đó ∆AED = ∆CEB (c.g.c).

b) Theo câu a ta có: ∆AED = ∆CEB

Suy ra $\overbrace{ADE}=\overbrace{EBC}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên suy ra AD // BC (đpcm).

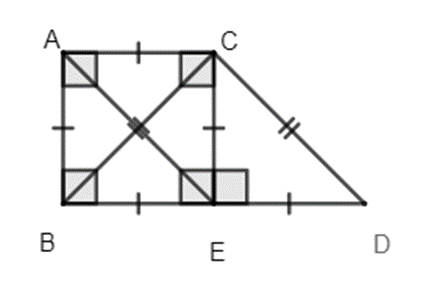
Bài 8. Kể tên các tam giác cân, tam giác vuông cân trong hình sau.

Hướng dẫn giải:

Trong hình vẽ có:

∙ 4 tam giác cân là: ∆BCD cân tại C; ∆BEC cân tại E; ∆ACE cân tại C; ∆CAB cân tại A.

∙ 4 tam giác vuông cân trong hình là: ∆BAC vuông cân tại A; ∆ACE vuông cân tại C; ∆CED vuông cân tại E; ∆CEB vuông cân tại E.

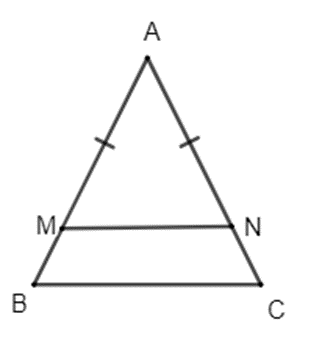
Bài 9. Cho tam giác ABC cân tại A và có $\overbrace{A}={40}^o$.

a) Tính $\overbrace{B};\overbrace{C}$.

b) Trên AB, AC lần lượt lấy hai điểm M (M $\in$ AB), N (N $\in$ AC) sao cho AB = AC. Chứng minh rằng: MN // BC.

Hướng dẫn giải:

a) Theo đề bài ta có: ∆ABC là tam giác cân tại A nên $\overbrace{B}=\overbrace{C}$.

Áp dụng định lý tổng ba góc trong tam giác, ta có:

$\overbrace{A}+\overbrace{B}+\overbrace{C}={180}^o$

Suy ra $\overbrace{B}+\overbrace{C}={180}^o-\overbrace{A}$

Do đó $\overbrace{B}=\overbrace{C}=\frac{{180}^o-\overbrace{A}}{2}=\frac{{180}^o-{40}^o}{2}={70}^o$.

Vậy $\overbrace{B}=\overbrace{C}={70}^o$.

b) Theo bài ra ta có: AM = AN.

Suy ra ∆AMN cân tại A.

Khi đó ta có: $\overbrace{M}=\overbrace{N}=\frac{{180}^o-\overbrace{A}}{2}={70}^o$.

Mà theo câu a ta có $\overbrace{B}=\overbrace{C}={70}^o$.

Suy ra $\overbrace{B}=\overbrace{C}=\overbrace{M}=\overbrace{N}$ hay $\overbrace{M}=\overbrace{B}$.

Mà góc M và B nằm ở vị trí đồng vị nên suy ra MN // BC (đpcm).

Bài 10. Cho hình vẽ:

Chứng minh rằng:

a) ∆ADB = ∆ADC.

b) AD là tia phân giác.

c) ∆DBC là tam giác cân.

Hướng dẫn giải:

a) Xét ∆ADB và ∆ADC có:

AB = AC (gt);

$\overbrace{ABD}=\overbrace{ACD}$ (gt);

Cạnh AD chung.

Do đó ∆ADB = ∆ADC (c.g.c).

b) Theo câu a ta có ∆ADB = ∆ADC.

Suy ra ta có $\overbrace{BAD}=\overbrace{CAD}$ (hai góc tương ứng).

Vậy AD là tia phân giác của góc $\overbrace{BAC}$.

c) Theo câu a ta có ∆ADB = ∆ADC

Suy ra BD = CD (hai cạnh tương ứng).

Xét ∆DBC có BD = CD suy ra ∆DBC cân tại D.

Bài 11.

a) So sánh các góc của tam giác ABC, biết AB = 3 cm, AC = 4 cm, BC = 5 cm.

b) So sánh các cạnh của tam giác ABC, biết $\overbrace{A}={90}^o,\overbrace{B}={30}^o$.

Hướng dẫn giải:

a) Ta thấy đối diện với các cạnh AB, AC, BC lần lượt là các góc C, B, A.

Mà theo đề bài ta có: AB < AC < BC (3 < 4 < 5).

Suy ra ta có $\overbrace{C}<\overbrace{B}<\overbrace{A}$.

Vậy $\overbrace{C}<\overbrace{B}<\overbrace{A}$.

b) Xét ∆ABC có: $\overbrace{A}+\overbrace{B}+\overbrace{C}={180}^o$

$\overbrace{C}={180}^o-\overbrace{A}-\overbrace{B}={180}^o-{90}^o-{30}^o={60}^o$.

Mặt khác ta có đối diện với các góc A, B, C lần lượt là các cạnh BC, AC, AB.

Mà $\overbrace{A}>\overbrace{C}>\overbrace{B}$ suy ra BC > AB > AC.

Vậy BC > AB > AC.

Bài 12. Cho tam giác ABC cân tại A có $\overbrace{C}={30}^o$.

a) Tìm cạnh lớn nhất trong ∆ABC.

b) Kẻ đường cao AH của tam giác ABC . Lấy điểm K bất kì thuộc BC. So sánh AH và AK.

Hướng dẫn giải:

a) Theo bài cho ta có tam giác ABC cân tại A.

Suy ra ta có: $\overbrace{B}=\overbrace{C}={30}^o$.

Mặt khác $\overbrace{A}={180}^o-\overbrace{B}-\overbrace{C}={180}^o-{30}^o-{30}^o={120}^o$.

Các cạnh đối diện với các góc A, B, C lần lượt là BC, AC, AB.

Mà ta có góc A là góc lớn nhất trong ∆ABC (120° > 30°).

Do đó cạnh lớn nhất trong ∆ABC là BC.

b) Ta thấy đoạn thẳng AH là đoạn vuông góc của đường thẳng BC, AK là đường xiên của đường thẳng BC.

Từ đó suy ra AK > AH.

Bài 13. Cho hình vẽ sau:

a) Tìm đoạn thẳng ngắn nhất trong các đoạn thẳng AD, AG, AC.

b) Tìm đoạn thẳng ngắn nhất trong các đoạn thẳng GD, GE, GA.

c) Chứng minh DG < AC.

Hướng dẫn giải:

a) Ta thấy AD là đường vuông góc, AG, AC là đường xiên kẻ từ A.

Suy ra đoạn thẳng ngắn nhất là AD.

b) Tương tự ta thấy GD là đường vuông góc, GE, GA là các đường xiên kẻ từ G.

Suy ra GD là đoạn thẳng ngắn nhất trong các đoạn thẳng GD, GE, GA.

c) Theo câu b ta có GD < GA hay AG > DG.

Xét ∆DGA vuông tại D nên $\overbrace{DGA}$ là góc nhọn.

Mặt khác $\overbrace{DGA}+\overbrace{AGC}={180}^o$ suy ra $\overbrace{AGC}$ là góc tù.

Xét ∆AGC có $\overbrace{AGC}$ là góc tù nên suy ra AC là cạnh có độ dài lớn nhất.

Suy ra AC > AG mà AG > DG nên ta có AC > DG.

Vậy DG < AC.

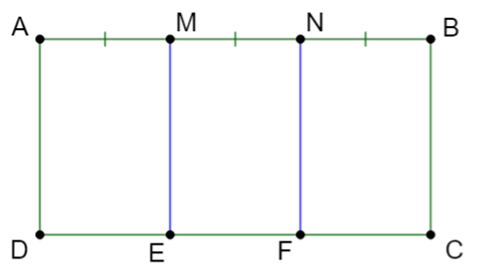
Bài 14. Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N và trên cạnh DC lấy các điểm E, F. Cho biết AM = MN = NB và ME, NF đều song song với AD. Tìm đường trung trực của mỗi đoạn thẳng AN và MB.

Hướng dẫn giải

Xét hình chữ nhật ABCD có AB vuông góc với AD.

Mà ME và NF đều song song với AD nên suy ra ME và NF đều vuông góc với AB.

+) Xét ME vuông góc với đoạn thẳng AB nên cũng vuông góc với đoạn thẳng AN tại trung điểm M của AN nên ME là đường trung trực của đoạn thẳng AM.

+) Xét NF vuông góc với đoạn thẳng AB nên cũng vuông góc với đoạn thẳng MB tại trung điểm N của MB nên NF là đường trung trực của đoạn thẳng MB.

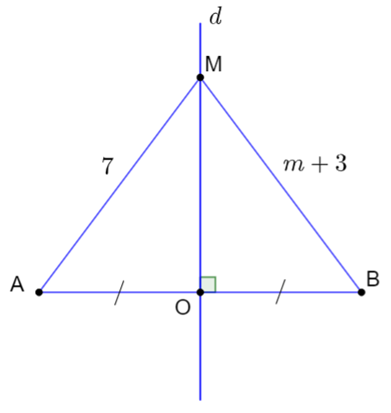
Bài 15. Trong hình vẽ dưới đây, cho d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = 7 và MB = m + 3. Tính m.

Hướng dẫn giải

Áp dụng định lí 1, với điểm M nằm trên đường thẳng trung trực của đoạn thẳng AB thì M cách đều hai đầu mút A, B nên suy ra

Điểm M nằm trên đường thẳng trung trực của đoạn thẳng AB thì M cách đều hai đầu mút A, B nên suy ra

MA = MB

Hay 7 = m + 3

Do đó m = 7 - 3 = 4

Vây giá trị của m là 4.

Bài 16. Cho C, D là hai điểm nằm trên đường trung trực của đoạn thẳng AB. CD giao AB tại E. Chứng minh hai tam giác CAD và CBD bằng nhau.

Hướng dẫn giải

Hai điểm C, D nằm trên đường trung trực của đoạn thẳng AB nên lần lượt cách đều hai đầu mút A và B.

Suy ra CA = CB và DA = DB

Xét hai tam giác CAD và CBD có

CA = CB (cmt)

DA = DB (cmt)

CD: cạnh chung

Suy ra $∆$CAD = $∆$CBD (c.c.c).

Bài 17.Xác định điểm O cách đều ba đỉnh của một tam giác vuông và nhận xét vị trí của điểm O trong trường hợp này.

Hướng dẫn giải

Xét tam giác ABC vuông tại B.

Điểm O cách đều ba đỉnh A, B, C của tam giác nên theo định lí ta suy ra được O là giao của ba đường trung trực của tam giác ABC.

Sau khi vẽ được hình như trên ta nhận xét được O cũng chính là trung điểm của cạnh AC.

Bài 18. Gọi O là giao điểm của hai đường trung trực của tam giác ABC. Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua hai điểm B và C hay không?

Hướng dẫn giải

Ta có: O là giao điểm của hai đường trung trực ứng với cạnh AB và AC của tam giác ABC nên suy O nằm trên hai đường trung trực của hai đoạn thẳng AB và AC

+) Vì O nằm trên đường trung trực ứng với cạnh AB nên O cách đều hai đầu mút A, B. Suy ra: OA = OB (1)

+) Vì O nằm trên đường trung trực ứng với cạnh AC nên O cách đều hai đầu mút A, C. Suy ra: OA = OC (2)

Từ (1) và (2) suy ra OB = OC (= OA).

Vậy suy ra đường tròn tâm O phải đi qua hai điểm B và C.

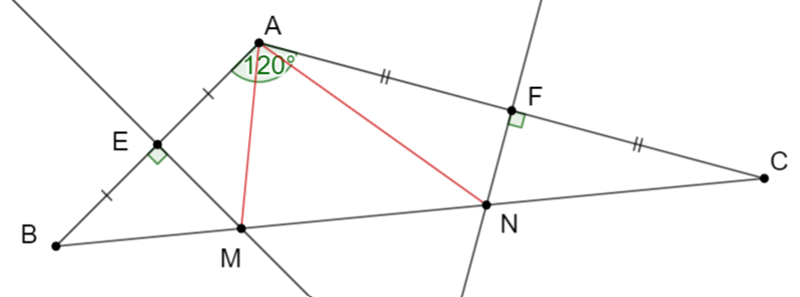
Bài 19. Cho tam giác ABC có góc A bằng 120°. Các đường trung trực của AB và AC lần lượt cắt BC tại M và N. Tính số đo góc MAN.

Hướng dẫn giải

Ta có M, N lần lượt nằm trên đường trung trực ứng với hai cạnh AB và AC nên suy ra:

MA = MB và NA = NC.

+) Vì MA = MB nên suy ra tam giác MAB cân tại A. Từ đó ta có

$\overbrace{MAB}=\overbrace{MBA}$ (1)

+) Vì NA = NC nên suy ra tam giác NAC cân tại A. Từ đó ta có

$\overbrace{NAC}=\overbrace{NCA}$ (2)

Xét tam giác ABC có:

$\overbrace{BAC}+\overbrace{ACB}+\overbrace{ABC}={180}^o$

$\Rightarrow {120}^o+\overbrace{ACB}+\overbrace{ABC}={180}^o$

$\iff \overbrace{ACB}+\overbrace{ABC}={180}^o-{120}^o={60}^o\left(3\right)$

Thay (1) và (2) vào (3) ta suy ra được

$\iff \overbrace{MBA}+\overbrace{NAC}={60}^o$ (4)

Lại có: $\overbrace{BAC}=\overbrace{MBA}+\overbrace{MAN}+\overbrace{NAC}={120}^o$

$\iff \overbrace{MAN}={120}^o-(\overbrace{MBA}+\overbrace{NAC})$ (5)

Thay (4) vào (5) ta có: $\overbrace{MAN}={120}^o-{60}^o={60}^o$.

Vậy $\overbrace{MAN}={60}^o.$

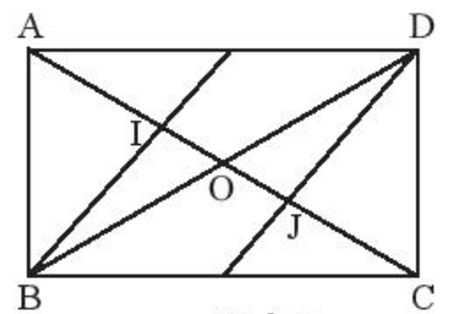
Bài 20. Cho hình chữ nhật ABCD, có I và J lần lượt là trọng tâm các tam giác ABD và CBD. Chứng minh AI = IJ = JC.

Hướng dẫn giải

Gọi O là giao điểm hai đường chéo của hình chữ nhật, nên ta có AO = BO.

+) Ta có I là trọng tâm của tam giác ABD, suy ra:

$AI=\frac{2}{3}AO;IO=AO-AI=\frac{1}{3}AO.$ (1)

+) Ta có J là trọng tâm của tam giác CBD, suy ra:

$JC=\frac{2}{3}CO=\frac{2}{3}AO;OJ=CO-JC=\frac{1}{3}CO=\frac{1}{3}AO.$ (2)

Vậy suy ra $IJ=IO+OJ=\frac{1}{3}AO+\frac{1}{3}AO=\frac{2}{3}AO.$ (3)

Từ (1), (2) và (3) suy ra: $AI=IJ=IC=\frac{2}{3}AO$.

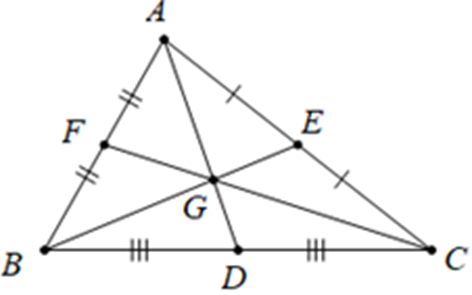
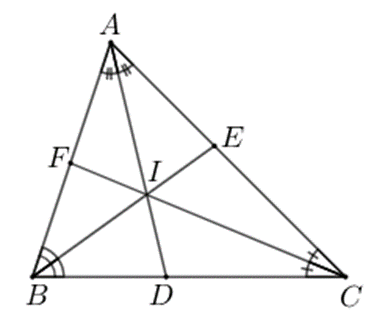
Bài 21. Cho tam giác ABC có ba đường trung tuyến AD, BE, CF đồng quy tại G. Chứng minh: $GA+GB+GC=\frac{2}{3}(AD+BE+CF).$

Hướng dẫn giải

Trong tam giác ABC, các đường trung tuyến AD, BE, CF cùng đi qua điểm G. Điểm G gọi là trọng tâm của tam giác ABC.

Ta có: $\frac{AG}{AD}=\frac{BG}{BE}=\frac{CG}{CF}=\frac{2}{3}$.

Suy ra $GA=\frac{2}{3}AD;GB=\frac{2}{3}BE;GC=\frac{2}{3}CF$.

Từ đó ta có: $GA+GB+GC=\frac{2}{3}(AD+BE+CF).$

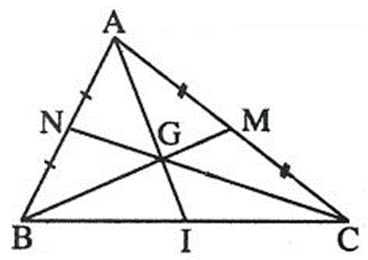
Bài 22. Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G.

a) Biết BM = 9 cm, tính BG.

b) Biết GN = 2 cm, tính CN.

c) Tìm x biết BG = 3x, GM = x + 1.

Hướng dẫn giải

a) G là trọng tâm của tam giác ABC nên suy ra:

$BG=\frac{2}{3}BM=\frac{2}{3}.9=6\left(cm\right).$

b) G là trọng tâm của tam giác ABC nên suy ra: $CG=\frac{2}{3}CN$.

Từ đó $GN=CN-CG=CN-\frac{2}{3}CN=\frac{1}{3}CN$.

Hay: $2=\frac{1}{3}CN$.

Vậy suy ra CN = 2.3 = 6 (cm).

c) Ta có: BM = BG + GM

Suy ra: 9 = 3x + (x + 1)

Hay 4x + 1 = 9

Tương đương với 4x = 9 - 1 = 8

Vậy suy ra: x = 8 : 4 = 2.

Bài 23. Cho tam giác ABC cân tại A, đường trung tuyến AM và đường cao BK. Gọi H là giao điểm của AM và BK. Chứng minh rằng CH vuông góc với AB.

Hướng dẫn giải

Vì tam giác ABC cân tại A nên đường trung tuyến AM cũng là đường cao của ABC.

Ta có H là giao điểm của hai đường cao AM và BK nên H là trực tâm của tam giác ABC

Suy ra CH là đường cao của tam giác ABC

Vậy CH vuông góc với AB.

Bài 24.Cho tam giác ABC cân tại A có góc A nhọn và H là trực tâm. Cho biết $\overbrace{BHC}={150}^o.$ Tìm các góc của tam giác ABC.

Hướng dẫn giải

Tam giác ABC cân tại A có AD là đường cao đồng thời là đường trung trực.

Do đó điểm H thuộc đường trung trực của đoạn thẳng BC thì cách đều hai đầu mút B và C.

Vậy suy ra HB = HD. Từ đó ta có tam giác HBD cân tại H.

Suy ra $\overbrace{HBC}=\overbrace{HCB}$.

Ta có: $\overbrace{HBC}+\overbrace{HCB}+\overbrace{BHC}={180}^o$.

Suy ra $\overbrace{HBC}=\overbrace{HCB}=\frac{{180}^o-\overbrace{BHC}}{2}=\frac{{180}^o-{150}^o}{2}={15}^o$.

Xét ∆EBC vuông tại E có: $\overbrace{EBC}+\overbrace{ECB}={90}^o$.

Hay $\overbrace{ECB}=\overbrace{ACB}={90}^o-\overbrace{EBC}={90}^o-{15}^o={75}^o$.

Vậy suy ra $\overbrace{ABC}=\overbrace{ACB}={75}^o$.

Xét tam giác ABC có:

$\overbrace{BAC}={180}^o-\overbrace{ABC}-\overbrace{ACB}={180}^o-{75}^o-{75}^o={30}^o$.

Bài 25. Cho hình vẽ dưới đây. Chứng minh AC, EK và BD cùng đi qua một điểm.

Hướng dẫn giải

Xét tam giác ABE có AC vuông góc với cạnh EB, EK vuông góc với cạnh AB và BD vuông góc với cạnh AE.

Nên suy ra ba đoạn thẳng AC, EK, BD là ba đường cao của tam giác AEB.

Vậy AC, EK, BD cùng đi qua một điểm và điểm đó chính là trực tâm của tam giác AEB.

Bài 26. Cho tam gáic ABC có ba đường phân giác AD, BE, CF đồng qui tại I. Biết góc BIC bằng 125°. Tính góc A.

Hướng dẫn giải

Xét tam giác BIC ta có:

$\overbrace{IBC}+\overbrace{ICB}={180}^o-\overbrace{BIC}={180}^o-{125}^o={55}^o$.

Do BI và CI là phân giác của góc B và C của tam giác ABC nên ta có:

$\overbrace{ABC}+\overbrace{ACB}=2(\overbrace{IBC}+\overbrace{ICB})=2.{55}^o={110}^o$.

Xét tam giác ABC ta có:

$\overbrace{BAC}={180}^o-(\overbrace{ABC}+\overbrace{ACB})={180}^o-{110}^o={70}^o$.

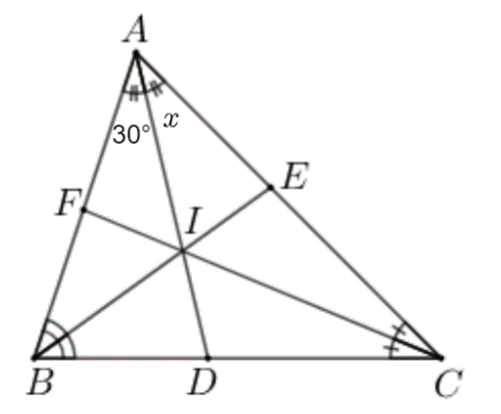
Bài 27.Tìm số đo x trong hình vẽ dưới đây.

Hướng dẫn giải

Ta có điểm I là giao điểm của hai phân giác góc B và C của tam giác BAC, suy ra AI cũng là phân giác góc A.

Vậy ta có: $\overbrace{BAD}=\overbrace{DAC}$

Hay x = 30°.

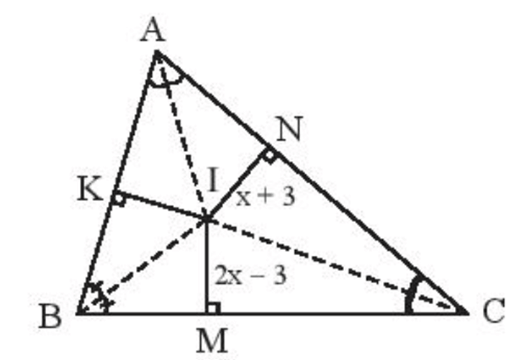
Bài 29. Cho I là giao điểm ba đường phân giác của tam giác ABC. Biết IN = x + 3, IM = 2x - 3. Tìm x.

Hướng dẫn giải

I là giao điểm ba đường phân giác của tam giác ABC nên suy ra I cách đều ba cạnh của tam giác ABC

Vậy suy ra IM = IN

Hay: 2x - 3 = x + 3

Tương đương: 2x - x = 3 + 3

Suy ra x = 6 là giá trị cần tìm.

Học tốt Toán 7 Chương 8

Các bài học để học tốt Chương 8 Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài tập cuối chương 8

• Giải sbt Toán 7 Bài tập cuối chương 8