Số vô tỉ. Căn bậc hai số học (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Số vô tỉ. Căn bậc hai số học (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Số vô tỉ. Căn bậc hai số học

1. Biểu diễn thập phân của một số hữu tỉ

Với một số hữu tỉ $\frac{a}{b}$, ta chỉ có hai trường hợp sau:

Trường hợp 1: Nếu $\frac{a}{b}$ bằng một phân số thập phân thì kết quả của phép chia $\frac{a}{b}$ là số thập phân bằng với phân số thập phân đó.

Ví dụ:

$\frac{2}{5}=\frac{4}{10}=0,4$; $\frac{3}{25}=\frac{12}{100}=0,12$.

Khi đó, các số 0,4 và 0,12 được gọi là số thập phân hữu hạn.

Trường hợp 2: Nếu $\frac{a}{b}$ không bằng bất cứ phân số thập phân nào thì kết quả của phép chia $\frac{a}{b}$ không bao giờ dừng và có chữ số hoặc cụm chữ số sau dấu phẩy lặp đi lặp lại.

Ví dụ:

a) Ta thực hiện phép chia 5 : 12 = 0,41666…; số 6 được lặp đi lặp lại mãi mãi.

Khi đó, ta viết $\frac{5}{12}=0,\mathrm{41666...}=0,41\left(6\right)$.

b) Ta thực hiện phép chia 7 : 30 = 0,2333… ; chữ số 3 lặp đi lặp lại mãi mãi.

Khi đó, ta viết $\frac{7}{30}=0,\mathrm{2333...}=0,2\left(3\right)$.

Do đó các số 0,41(6); 0,2(3) gọi là các số thập phân vô hạn tuần hoàn và chữ số lặp đi lặp lại như (6); (3) được gọi là chu kì.

Chú ý: Số 0,41(6) đọc là 0,41 chu kì 6 ; số 0,2(3) đọc là 0,2 chu kì 3.

•Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ: $\frac{12}{25}=\frac{48}{100}=0,48$; $\frac{10}{9}=1,\left(1\right)$

2. Số vô tỉ

– Số thập phân vô hạn mà ở phần thập phân của nó không có một chu kì nào cả được gọi là số thập phân vô hạn không tuần hoàn.

– Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.

– Tập hợp các số vô tỉ kí hiệu là I.

Ví dụ:

a) Với x² = 2 người ta tính được x = 1,414213562… là số thập phân vô hạn không tuần hoàn.

Vậy x = 1,414213562… là số vô tỉ.

b) Số Pi (π) là tỉ số giữa chu vi của một đường tròn với độ dài đường kính của đường tròn đó.

Người ta tính được π = 3,14159265358979323846264338… là số thập phân vô hạn không tuần hoàn.

Vậy π là một số vô tỉ.

3. Căn bậc hai số học

– Căn bậc hai số học của một số a không âm là số x không âm sao cho x² = a.

– Căn bậc hai số học của số a được kí hiệu là $\sqrt{a}$.

– Một số không âm có đúng một căn bậc hai số học.

Chú ý:

– Số âm không có căn bậc hai số học.

– Ta có $\sqrt{a}$ ≥ 0 với mọi số a không âm.

– Với mọi số a không âm, ta luôn có ${\left(\sqrt{a}\right)}^2=a$, ví dụ ${\left(\sqrt{2}\right)}^2=2$.

– Ta có $\sqrt{2}$ là độ dài đường chéo của một hình vuông có cạnh bằng 1.

Ví dụ: $\sqrt{4}=2$ ; $\sqrt{81}=9$ ; $\sqrt{0}=0$.

4. Tính căn bậc hai số học bằng máy tính cầm tay

Ta có thể tính giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số nguyên dương bằng máy tính cầm tay.

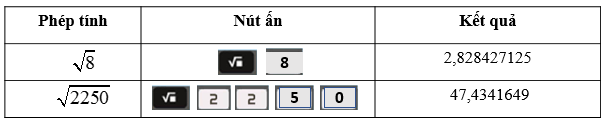
Ví dụ : Dùng máy tính cầm tay ta tính $\sqrt{8}$ và $\sqrt{2250}$ như sau:

Vậy $\sqrt{8}$ ≈ 2,828427125; $\sqrt{2250}$ ≈ 47,4341649.

Bài tập Số vô tỉ. Căn bậc hai số học

Bài 1: Hãy biểu diễn các số hữu tỉ sau dưới dạng số thập phân $\frac{11}{40}$; $\frac{14}{25}$; $\frac{2}{3}$; $-\frac{4}{3}$. Hãy chỉ ra số nào là số thập hữu hạn, số nào là số thập phân vô hạn tuần hoàn.

Hướng dẫn giải

Ta có: $\frac{11}{40}=\frac{275}{1000}=0,275$. Số 0,275 là số thập phân hữu hạn.

Ta có : $\frac{14}{25}=\frac{56}{100}=0,56$. Số 0,56 là số thập phân hữu hạn.

Ta có : $\frac{2}{3}=0,\left(6\right)$. Số 0,(6) là số thập phân vô hạn tuần hoàn với chu kì là 6.

Ta có : $-\frac{4}{3}=-1,\left(3\right)$. Số –1,(3) là số thập phân vô hạn tuần hoàn với chu kì là 3.

Vậy các số thập phân hữu hạn là $\frac{11}{40}$;$\frac{14}{25}$ và các số thập phân vô hạn tuần hoàn là $\frac{2}{3}$; $-\frac{4}{3}$

Bài 2: Tính

a) $\sqrt{16}$;

b) $\sqrt{{(-12)}^2}$.

Hướng dẫn giải

a) Ta có: $\sqrt{16}=4$ (vì 4 > 0 và 4² =16).

b) Ta có: $\sqrt{{(-12)}^2}=\sqrt{144}=12$ (vì 12 > 0 và 12² = 144).

Bài 3: Hãy dùng máy tính cầm tay tính $\sqrt{5}$; $\sqrt{625}$ .

Hướng dẫn giải

Sử dụng máy tính cầm tay ta tính được:

$\sqrt{5}$≈ 2,2360679.

$\sqrt{625}$ = 25.

Học tốt Số vô tỉ. Căn bậc hai số học

Các bài học để học tốt Số vô tỉ. Căn bậc hai số học Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học

• Giải sbt Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học