Tam giác bằng nhau (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 2: Tam giác bằng nhau hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tam giác bằng nhau (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Tam giác bằng nhau

1. Định nghĩa:

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

* Chú ý:

- Khi vẽ hai tam giác bằng nhau, các cạnh hoặc các góc bằng nhau được đánh dấu bởi những kí hiệu giống nhau.

- Khi dùng kí hiệu hai tam giác bằng nhau, ta phải viết các đỉnh tương ứng theo cùng thứ tự.

Ví dụ: Cho hai tam giác ABC và FDE là hai tam giác bằng nhau.

Kí hiệu là ∆ABC = ∆FDE.

Khi đó ta có:

AB = FD; BC = DE; AC = FE; $\overbrace{A}=\overbrace{F};\overbrace{B}=\overbrace{D};\overbrace{C}=\overbrace{E}$.

2. Các trường hợp bằng nhau của hai tam giác

* Trường hợp bằng nhau thứ nhất: cạnh – cạnh – cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

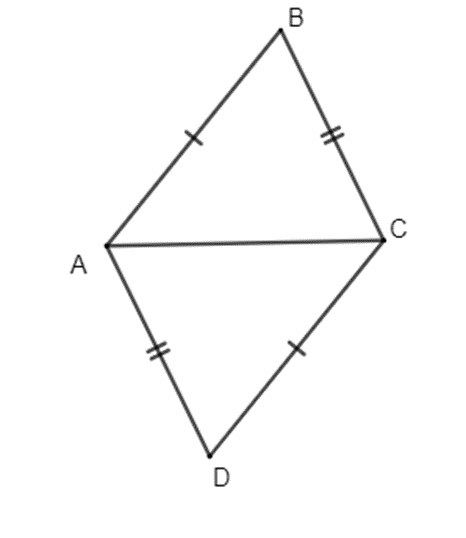
Ví dụ: Cho hình sau:

Xét ∆ABC và ∆CDA có:

AB = CD (gt);

Cạnh AC chung;

BC = AD (gt)

Do đó: ∆ABC = ∆CDA(c.c.c).

*Trường hợp bằng nhau thứ hai: cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

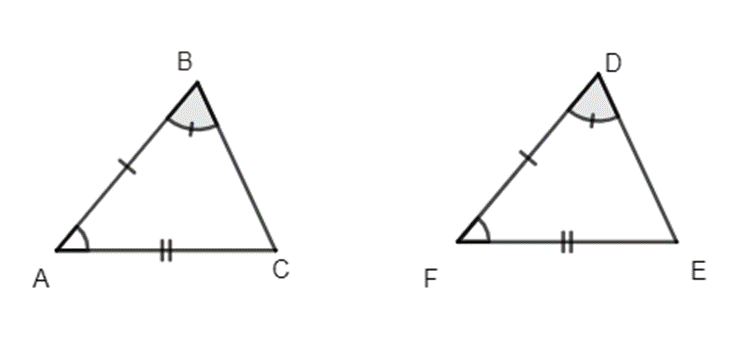
Ví dụ: Xét hai tam giác sau:

Xét ∆ABC và ∆FDE ta có:

AB = FD (gt);

$\overbrace{A}=\overbrace{F}$ (gt);

AC = FE (gt)

Do đó ∆ABC = ∆FDE (c.g.c).

* Trường hợp bằng nhau thứ ba: góc – cạnh – góc (g.c.g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

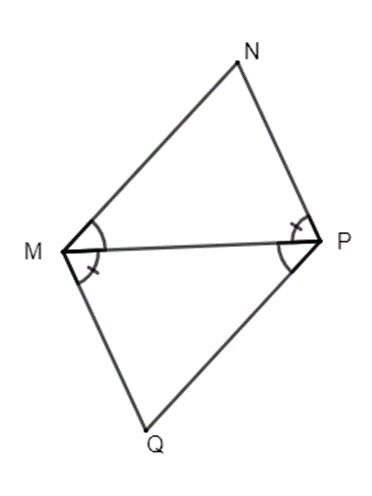
Ví dụ: Cho hình sau:

Xét ∆MNP và ∆PQM ta có:

$\overbrace{\mathrm{NMP}}=\overbrace{\mathrm{QPM}}$ (gt);

Cạnh MP chung;

$\overbrace{\mathrm{NPM}}=\overbrace{\mathrm{QMP}}$ (gt)

Do đó ∆MNP = ∆PQM (g.c.g).

3. Các trường hợp bằng nhau của hai tam giác vuông

* Trường hợp hai cạnh góc vuông:

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp c.g.c).

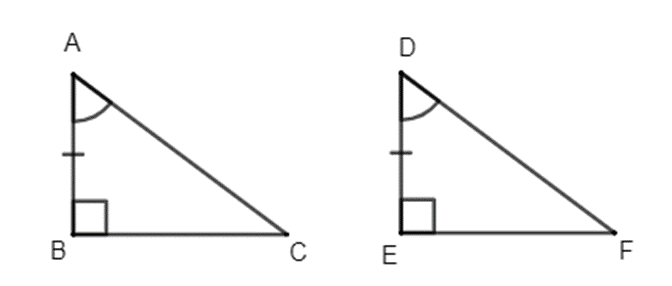
Ví dụ: Cho hình vẽ:

Xét ∆ABC và ∆EDF ta có:

$\overbrace{A}=\overbrace{E}={90}^o$;

AC = EF (gt);

AB = DE (gt)

Do đó ∆ABC = ∆EDF (c.g.c)

* Trường hợp một cạnh góc vuông và một góc nhọn:

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp g.c.g).

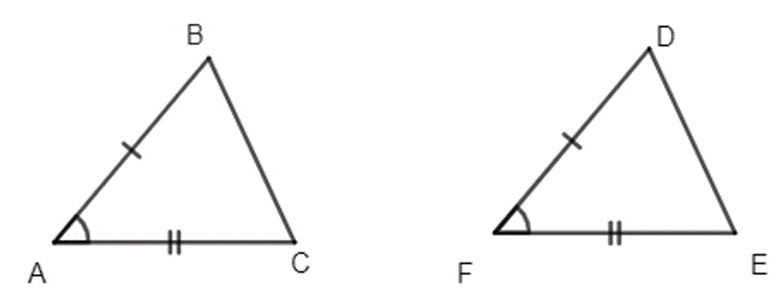
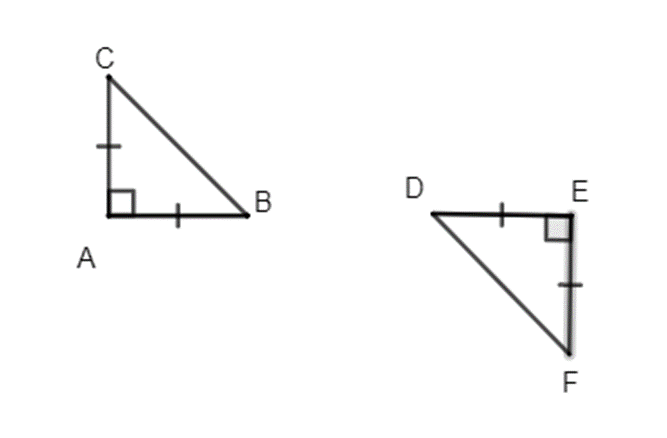
Ví dụ:Cho hình sau:

Xét ∆ABC vuông tại B và ∆DEF vuông tại E, ta có:

AB = DE (gt);

$\overbrace{A}=\overbrace{D}$ (gt)

Do đó ∆ABC = ∆DEF (g.c.g).

* Trường hợp cạnh huyền và một cạnh góc vuông:

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Ví dụ: Cho hình vẽ:

Xét ∆ABC và ∆DBC đều vuông tại B có:

AC = DC (gt);

Cạnh BC chung.

Do đó ∆ABC = ∆DBC (cạnh huyền – cạnh góc vuông).

Bài tập Tam giác bằng nhau

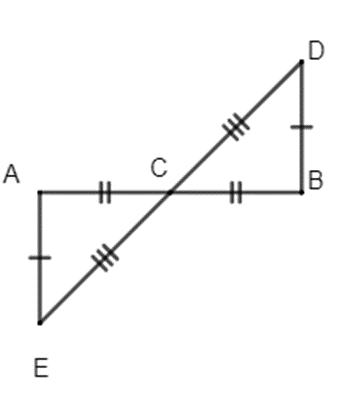
Bài 1. Quan sát hình sau và điền vào chỗ trống:

a) ∆ACE = …;

b) ∆EAC = …;

c) ∆CAE = ….

Hướng dẫn giải:

Theo hình vẽ trên ta có:

AC = BC; CD = CE; AE = BD.

Do đó: ∆ACE = ∆BCD (c.c.c);∆EAC = ∆DBC (c.c.c);∆CAE = ∆CBD (c.c.c).

Vậy ta điền vào như sau:

a) ∆ACE = ∆BCD;

b) ∆EAC = ∆DBC;

c) ∆CAE = ∆CBD.

Bài 2. Cho ∆FCG = ∆MNQ và $\overbrace{G}={30}^o$, CG = 4 cm, MN = 3 cm. Tính số đo <![if !vml]><![endif]> và độ dài NQ, FC.

Hướng dẫn giải:

Theo bài cho ta có ∆FCG = ∆MNQ.

Suy ra ta có: $\overbrace{G}=\overbrace{Q}={30}^o$;

CG = NQ = 4 cm;

FC = MN = 3 cm.

Vậy $\overbrace{Q}={30}^o$; NQ = 4 cm; MN = 3 cm.

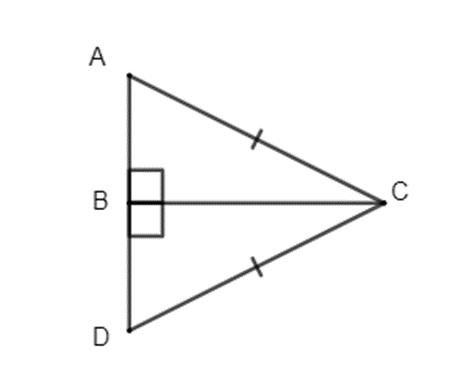
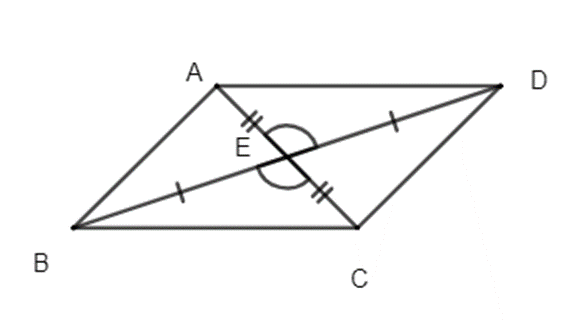
Bài 3. Cho hình sau:

Chứng minh rằng:

a) ∆AED = ∆CEB;

b) AD // BC.

Hướng dẫn giải:

a) Xét ∆AED và ∆CEB có:

AE = CE (gt);

$\overbrace{AED}=\overbrace{CEB}$ (gt);

BE = DE (gt)

Do đó ∆AED = ∆CEB (c.g.c).

b) Theo câu a ta có: ∆AED = ∆CEB

Suy ra $\overbrace{ADE}=\overbrace{EBC}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên suy ra AD // BC (đpcm).

Học tốt Tam giác bằng nhau

Các bài học để học tốt Tam giác bằng nhau Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 2: Tam giác bằng nhau

• Giải sbt Toán 7 Bài 2: Tam giác bằng nhau