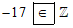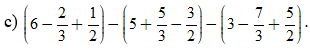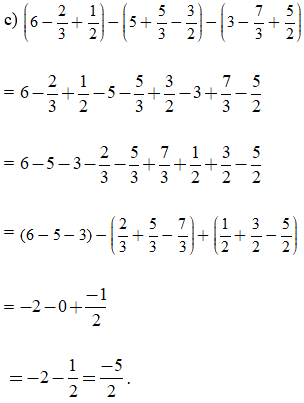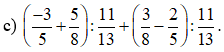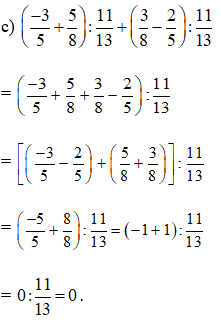Tổng hợp lý thuyết Toán 7 Chương 1 Chân trời sáng tạo

---

Với tổng hợp lý thuyết Toán lớp 7 Chương 1: Số hữu tỉ hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tổng hợp lý thuyết Toán 7 Chương 1 Chân trời sáng tạo

Lý thuyết tổng hợp Toán 7 Chương 1

1. Số hữu tỉ

Số hữu tỉ là số được viết dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ, b ≠ 0. Các phân số bằng nhau biểu diễn cùng một số hữu tỉ.

Tập hợp các số hữu tỉ được kí hiệu là ℚ.

Chú ý: Mỗi số nguyên là một số hữu tỉ.

2. Thứ tự trong tập hợp số hữu tỉ

- Với hai số hữu tỉ bất kì x, y ta luôn có: hoặc x = y hoặc x < y hoặc y > x.

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

Số hữu tỉ bé hơn 0 gọi là số hữu tỉ âm.

Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

Chú ý: Số hữu tỉ dương luôn luôn lớn hơn số hữu tỉ âm.

3. Biểu diễn số hữu tỉ trên trục số

- Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.

- Với hai số hữu tỉ bất kì x, y, nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

4. Số đối của một số hữu tỉ

Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.

Số đối của số hữu tỉ x kí hiệu là −x.

Chú ý:

Mọi số hữu tỉ đều có một số đối.

Số đối của số 0 là số 0.

Với hai số hữu tỉ âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

5. Cộng, trừ hai số hữu tỉ

Để cộng, trừ hai số hữu tỉ x, y, ta có thể viết chúng dưới dạng hai phân số rồi áp dụng quy tắc cộng, trừ phân số.

6. Tính chất của phép cộng số hữu tỉ

Phép cộng số hữu tỉ cũng có các tính chất như phép cộng số nguyên: giao hoán, kết hợp và cộng với số 0.

7. Nhân hai số hữu tỉ

Cho x, y là hai số hữu tỉ: x = $\frac{a}{b}$, y = $\frac{c}{d}$, ta có x . y = $\frac{a}{b}$. $\frac{c}{d}$ = $\frac{a.c}{b.d}$.

8. Tính chất của phép nhân số hữu tỉ

Phép nhân số hữu tỉ cũng có các tính chất như phép nhân số nguyên: giao hoán, kết hợp, nhân với số 1, tính chất phân phối của phép nhân đối với phép cộng.

9. Chia hai số hữu tỉ

Cho x, y là hai số hữu tỉ: x = $\frac{a}{b}$ , y = $\frac{c}{d}$ (y ≠ 0), ta có x : y = $\frac{a}{b}:\frac{c}{d}$ = $\frac{a}{b}.\frac{d}{c}=\frac{a.d}{b.c}$.

Chú ý:

Thương của phép chia số hữu tỉ x cho số hữu tỉ y (y ≠ 0) gọi là tỉ số của hai số x và y, kí hiệu là $\frac{x}{y}$ hay x : y.

10. Luỹ thừa với số mũ tự nhiên

Luỹ thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ , là tích của n thừa số x.

xⁿ = $\underset{n}{\underbrace{x.x.x\mathrm{.....}x}}$ ( x ∈ ℚ, n ∈ ℕ, n >1)

Ta đọc xⁿ là “x mũ n” hoặc “x luỹ thừa n” hoặc “luỹ thừa bậc n của x”,

Số x được gọi là cơ số, n gọi là số mũ.

Quy ước: x¹ = x

x⁰ = 1 (x ≠ 0)

Chú ý:

Khi viết số hữu tỉ x dưới dạng $\frac{a}{b}$ (a, b ∈ ℤ, b ≠ 0), ta có:

${\left(\frac{a}{b}\right)}^n=\underset{n}{\underbrace{\stackrel{n}{\overbrace{\frac{a.a\mathrm{.....}a}{b.b\mathrm{.....}b}}}}}=\frac{a^n}{b^n}$

11. Tích và thương của hai luỹ thừa cùng cơ số

Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

x^m . xⁿ = x^m+n

Khi chia hai luỹ thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của luỹ thừa bị chia trừ đi số mũ của luỹ thừa chia.

x^m : xⁿ = x^{m – n} (x ≠ 0, m ≥ n)

12. Luỹ thừa của luỹ thừa

Khi tính luỹ thừa của một luỹ thừa, ta giữ nguyên cơ số và nhân hai số mũ.

(x^m )ⁿ = x^m.n

13. Quy tắc dấu ngoặc

Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc:

Có dấu “+”, thì vẫn giữ nguyên dấu của các số hạng trong ngoặc.

x + (y + z – t) = x + y + x – t

Có dấu “−”, thì phải đổi dấu tất cả các số hạng trong ngoặc.

x – (y + z – t) = x – y – z + t

14. Quy tắc chuyển vế

Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

Với mọi x, y, z ∈ ℚ: x + y = z ⇒ x = z – y;

15. Thứ tự thực hiện các phép tính

Thứ tự thực hiện các phép tính trong một biểu thức đối với biểu thức không có dấu ngoặc:

Nếu biểu thức chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.

Nếu biểu thức có các phép cộng, trừ, nhân, chia, nâng lên luỹ thừa, ta thực hiện:

Luỹ thừa → nhân và chia → cộng và trừ

Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc:

() → [] → {}

Bài tập tổng hợp Toán 7 Chương 1

Bài 1. Thay bằng kí hiệu ∈, ∉ thích hợp.

−7 ℕ ; −17 ℤ ; −38 ℚ ;

$\frac{4}{5}$ ℤ ; $\frac{4}{5}$ ℚ ; 0,25 ℤ ;

3,25 ℚ.

Hướng dẫn giải

Ta có – 7 là số nguyên âm nên –7 không thuộc ℕ. Do đó ta viết .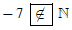

Ta có −17 là số nguyên âm nên −17 thuộc ℤ. Do đó ta viết

Ta có – 38 là số nguyên âm nên –38 thuộc ℚ. Do đó ta viết .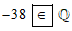

Ta có $\frac{4}{5}$ là số hữu tỉ nên $\frac{4}{5}$ không thuộc ℤ. Do đó ta viết .

Ta có $\frac{4}{5}$ là số hữu tỉ nên $\frac{4}{5}$ thuộc ℚ. Do đó ta viết .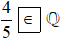

Ta có 0,25 là số hữu tỉ nên 0,25 không thuộc ℤ. Do đó ta viết .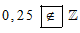

Ta có 3,25 là số hữu tỉ nên 3,25 thuộc ℚ. Do đó ta viết .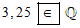

−7 ℕ ; −17 ℤ ; −38 ℚ ;

$\frac{4}{5}$ ℤ ; $\frac{4}{5}$ ℚ ; 0,25 ℤ ;

3,25 ℚ.

Bài 2.

a) Trong các phân số sau, phân số nào biểu diễn số hữu tỉ $\frac{-5}{9}$ ?

$\frac{-10}{18}$; $\frac{10}{18}$; $\frac{15}{-27}$; $-\frac{20}{36}$; $\frac{-25}{27}$.

b) Tìm số đối của mỗi số sau: 12; $\frac{4}{9}$ ; −0, 375; $\frac{0}{5}$; $-2\frac{2}{5}$.

Hướng dẫn giải

a) Ta có:

$\frac{-10}{18}=\frac{-10:2}{18:2}=\frac{-5}{9}$ ;

$\frac{10}{18}=\frac{10:2}{18:2}=\frac{5}{9}$;

$\frac{15}{-27}=\frac{15:3}{-27:3}$$=\frac{5}{-9}=\frac{-5}{9}$;

$-\frac{20}{36}=-\frac{20:4}{36:4}$$=-\frac{5}{9}=\frac{-5}{9}$;

Vậy các phân số biểu diễn số hữu tỉ $\frac{-5}{9}$ là: $\frac{-10}{18}$; $\frac{15}{-27}$; $-\frac{20}{36}$.

b)

Số đối của 12 là −12.

Số đối của $\frac{4}{9}$ là $\frac{-4}{9}$.

Số đối của −0,375 là– (−0,375) = 0,375.

Số đối của $\frac{0}{5}$ là $\frac{-0}{5}$.

Số đối của $-2\frac{2}{5}$ là $\frac{12}{5}$ và ta viết là $2\frac{2}{5}$.

Bài 3.

a) Các điểm A, B, C trong hình dưới biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ $\frac{-2}{5}$; $1\frac{1}{5}$; $\frac{3}{5}$; − 0,8 trên trục số.

Hướng dẫn giải

a) Dựa vào hình vẽ, ta thấy đoạn thẳng đơn vị cũ được chia thành 5 đoạn bằng nhau.

Ta được đoạn thẳng đơn vị mới bằng $\frac{1}{4}$ đoạn thẳng đơn vị cũ.

Điểm A nằm về bên trái gốc O và cách gốc O một đoạn bằng 7 đơn vị mới.

Khi đó, điểm A biểu diễn cho số hữu tỉ $-\frac{7}{4}$.

Điểm B nằm về bên phải gốc O và cách gốc O một đoạn bằng 3 đơn vị mới.

Khi đó, điểm B biểu diễn cho số hữu tỉ $\frac{3}{4}$.

Điểm C nằm về bên phải gốc O và cách gốc O một đoạn bằng 5 đơn vị mới.

Khi đó, điểm C biểu diễn cho số hữu tỉ $\frac{5}{4}$.

b) Ta có $1\frac{1}{5}=\frac{6}{5}$ ; − 0,8 = $-\frac{8}{10}=\frac{-4}{5}$.

Chia đoạn thẳng đơn vị cũ thành 5 đoạn bằng nhau ta được đoạn thẳng đơn vị mới bằng $\frac{1}{5}$ đoạn đơn vị cũ. Khi đó:

Điểm M là điểm biểu diễn cho số hữu tỉ $-\frac{2}{5}$ nên điểm M nằm về bên trái gốc O và cách gốc O một đoạn bằng 2 đơn vị mới.

Điểm N biểu diễn cho số hữu tỉ $1\frac{1}{5}$ nên điểm N nằm về bên phải gốc O và cách gốc O một đoạn bằng 6 đơn vị mới.

Điểm P biểu diễn cho số hữu tỉ $\frac{3}{5}$ nên điểm P nằm về bên phải gốc O và cách gốc O một đoạn bằng 3 đơn vị mới.

Điểm Q biểu diễn cho số hữu tỉ –0,8 nên điểm Q nằm về bên phải gốc O và cách gốc O một đoạn bằng 4 đơn vị mới.

Do đó ta có hình vẽ:

Bài 4.

a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

$\frac{5}{12}$; $\frac{-4}{5}$; $2\frac{2}{3}$; −2; $\frac{0}{234}$; −0,32.

b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.

Hướng dẫn giải

a)Số hữu tỉ dương là: $\frac{5}{12}$ ; $2\frac{2}{3}$.

Số hữu tỉ âm là: $\frac{-4}{5}$; −2; −0,32.

Số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: $\frac{0}{234}$.

b) Ta chia dãy số thành các nhóm sau:

Nhóm 1 là nhóm các số hữu tỉ âm: $\frac{-4}{5}$ ; −2; −0,32.

Ta có: $\frac{-4}{5}=\frac{-20}{25}$; −2 = $\frac{-2}{1}$ = $\frac{-10}{5}$ = $\frac{-50}{25}$;

−0,32 = $\frac{-32}{100}=-\frac{8}{25}$.

Vì –50 < –20 < –8

nên $\frac{-50}{25}<\frac{-20}{25}<-\frac{8}{25}$

Hay −2 < $\frac{-4}{5}$ < −0,32.

Nhóm 2 là nhóm các số hữu tỉ dương: $\frac{5}{12}$ ; $2\frac{2}{3}$.

Ta có: $\frac{5}{12}$; $2\frac{2}{3}=\frac{8}{3}=\frac{32}{12}$.

Vì 5 < 32 nên $\frac{5}{12}$ < $\frac{32}{12}$ hay $\frac{5}{12}$ < $2\frac{2}{3}$.

Nhóm 3 gồm số $\frac{0}{234}$.

Vì số hữu tỉ âm nhỏ hơn số 0 và nhỏ hơn số hữu tỉ dương nên ta có:

−2 < $\frac{-4}{5}$ < −0,32 < $\frac{0}{234}$< $\frac{5}{12}$ < $2\frac{2}{3}$.

Vậy theo thứ tự từ bé đến lớn ta có dãy số sau:−2; $\frac{-4}{5}$; −0,32; $\frac{0}{234}$; $\frac{5}{12}$; $2\frac{2}{3}$.

Bài 5. So sánh các cặp số hữu tỉ sau:

a) $\frac{2}{-5}$ và $\frac{-3}{8}$;

b) −0,85 và $\frac{-17}{20}$;

c) $\frac{-137}{200}$ và $\frac{37}{-25}$;

d) $-1\frac{3}{10}$ và $-\left(\frac{-10}{-13}\right)$.

Hướng dẫn giải

a) Ta có $\frac{2}{-5}=\frac{-16}{40}$; $\frac{-3}{8}=\frac{-15}{40}$.

Vì −16 < −15 và 40 > 0 nên $\frac{-16}{40}$< $\frac{-15}{40}$.

Vậy $\frac{2}{-5}$ < $\frac{-3}{8}$.

b) Ta có $-0,85=\frac{-85}{100}=\frac{-17}{20}$

nên −0,85 = $\frac{-17}{20}$.

Vậy −0,85 = $\frac{-17}{20}$.

c) Ta có $\frac{37}{-25}=\frac{-296}{200}$.

Vì −137 > −296 và 200 > 0

nên $\frac{-137}{200}$> $\frac{-296}{200}$.

Vậy $\frac{-137}{200}$ > $\frac{37}{-25}$.

d) Ta có $-1\frac{3}{10}=\frac{-13}{10}=\frac{-169}{130}$;

$-\left(\frac{-10}{-13}\right)=\frac{-10}{13}=\frac{-100}{130}$.

Vì −169 < −100 và 130 > 0,

nên $\frac{-169}{130}$< $\frac{-100}{130}$.

Vậy $-1\frac{3}{10}$ < $-\left(\frac{-10}{-13}\right)$.

Bài 6. So sánh các cặp số hữu tỉ sau:

a) $\frac{-2}{3}$ và $\frac{1}{200}$;

b) $\frac{139}{138}$ và $\frac{1375}{1376}$;

c) $\frac{-11}{33}$ và $\frac{25}{-76}$.

Hướng dẫn giải

a) Ta có $\frac{-2}{3}$ < 0; $\frac{1}{200}$ > 0 nên $\frac{-2}{3}$< $\frac{1}{200}$.

Vậy $\frac{-2}{3}$< $\frac{1}{200}$.

b) Ta có

$\frac{139}{138}>\frac{138}{138}=1$; $\frac{1375}{1376}<\frac{1376}{1376}=1$.

Do đó $\frac{139}{138}$> $\frac{1375}{1376}$.

Vậy $\frac{139}{138}$> $\frac{1375}{1376}$.

c) Ta có: $\frac{-11}{33}=\frac{-1}{3}=\frac{25}{-75}$.

Vì −75 > −76 và 25 > 0, nên $\frac{25}{-75}$< $\frac{25}{-76}$.

Vậy $\frac{-11}{33}$< $\frac{25}{-76}$.

Bài 7. Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.

a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto Rico. Giải thích.

b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên. Giải thích.

Hướng dẫn giải

a) Độ cao của rãnh Puerto Rico là: – 8,6 m.

Vì 7,7 < 8,0 < 8,6 nên −7,7 > −8,0 > −8,6.

Do đó những rãnh đại dương có độ cao cao hơn rãnh Puerto Rico là: Rãnh Romanche; Rãnh Peru – Chile.

Vậy những rãnh đại dương có độ cao cao hơn rãnh Puerto Rico là: Rãnh Romanche; Rãnh Peru – Chile.

b) Vì 7,7 < 8,0 < 8,6 < 10,5 nên −7,7 > −8,0 > −8,6 > –10,5.

Do đó rãnh đại dương có độ cao thấp nhất trong bốn rãnh trên là: Rãnh Philippine.

Vậy rãnh đại dương có độ cao thấp nhất trong bốn rãnh trên là: Rãnh Philippine.

Bài 8. Tính:

a) $\left(\frac{-1}{6}\right)+0,75$;

b) $\frac{-7}{8}-\left(-\frac{5}{24}\right)$;

c) $2\frac{3}{8}.\left(-0,4\right)$;

d) $\left(\frac{-12}{5}\right):\left(-6,5\right)$.

Hướng dẫn giải

a) $\left(\frac{-1}{6}\right)+0,75$

= $\left(\frac{-1}{6}\right)+\frac{75}{100}=\left(\frac{-1}{6}\right)+\frac{3}{4}$

= $\left(\frac{-2}{12}\right)+\frac{9}{12}=\frac{\left(-2\right)+9}{12}$

$=\frac{7}{12}$;

b) $\left(\frac{-7}{8}\right)-\left(-\frac{5}{24}\right)$

= $\frac{-21}{24}+\frac{5}{24}$

= $\frac{\left(-21\right)+5}{24}$

= $\frac{-16}{24}=\frac{-2}{3}$;

c) $2\frac{3}{8}.\left(-0,4\right)$

= $\frac{19}{8}.\left(\frac{-4}{10}\right)=\frac{19}{8}.\left(\frac{-2}{5}\right)$

= $\frac{19.\left(-2\right)}{8.5}=\frac{-38}{40}$

= $\frac{-19}{20}$;

d) $\left(\frac{-12}{5}\right):\left(-6,5\right)$

= $\left(\frac{-12}{5}\right):\left(-\frac{65}{10}\right)$

$=\frac{12}{5}:\frac{13}{2}$

= $\frac{12}{5}.\frac{2}{13}=\frac{24}{65}$.

Bài 9. Tính:

a) $\frac{3}{7}+\left(-\frac{5}{2}\right)+\left(-\frac{3}{5}\right)$;

b) $\frac{2}{3}-\left(\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right)$;

c) $\left(-2\right).\left(\frac{-38}{21}\right).\left(\frac{-7}{4}\right).\left(-\frac{3}{8}\right)$;

d) $\left(\frac{11}{22}:\frac{33}{16}\right).\frac{3}{5}$.

Hướng dẫn giải

a) $\frac{3}{7}+\left(-\frac{5}{2}\right)+\left(-\frac{3}{5}\right)$

= $\frac{3}{7}-\frac{5}{2}-\frac{3}{5}$

= $\frac{30}{70}-\frac{175}{70}-\frac{42}{70}$

= $\frac{-187}{70}$.

b) $\frac{2}{3}-\left(\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right)$

= $\frac{2}{3}-\left(\left(-\frac{7}{4}\right)-\left(\frac{4}{8}+\frac{3}{8}\right)\right)$

= $\frac{2}{3}-\left(\frac{-7}{4}-\frac{7}{8}\right)$

= $\frac{2}{3}-\left(\frac{-14}{8}-\frac{7}{8}\right)$

= $\frac{2}{3}-\frac{-21}{8}$

= $\frac{2}{3}+\frac{21}{8}$

= $\frac{16}{24}+\frac{63}{24}=\frac{79}{24}$.

c) $\left(-2\right).\left(\frac{-38}{21}\right).\left(\frac{-7}{4}\right).\left(-\frac{3}{8}\right)$

= $2.\frac{38}{21}.\frac{7}{4}.\frac{3}{8}$

= $\frac{2.38.7.3}{21.4.8}$

= $\frac{2.2.19.21}{21.2.2.8}=\frac{19}{8}$.

d) $\left(\frac{11}{22}:\frac{33}{16}\right).\frac{3}{5}$

= $\frac{11}{22}.\frac{16}{33}.\frac{3}{5}=\frac{11.16.3}{22.33.5}$

= $\frac{11.2.8.3}{2.11.3.11.5}=\frac{8}{55}$.

Bài 10. Tính:

a) $\left(\frac{-2}{3}+\frac{3}{7}\right):\frac{4}{5}+\left(\frac{-1}{3}+\frac{4}{7}\right):\frac{4}{5}$;

b) $\frac{5}{9}:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac{5}{9}:\left(\frac{1}{15}-\frac{2}{3}\right)$;

Hướng dẫn giải

a) $\left(\frac{-2}{3}+\frac{3}{7}\right):\frac{4}{5}+\left(\frac{-1}{3}+\frac{4}{7}\right):\frac{4}{5}$

= $\left(\frac{-2}{3}+\frac{3}{7}+\frac{-1}{3}+\frac{4}{7}\right):\frac{4}{5}$

= $\left(\left(\frac{-2}{3}+\frac{-1}{3}\right)+\left(\frac{3}{7}+\frac{4}{7}\right)\right):\frac{4}{5}$

= $\left(\frac{-3}{3}+\frac{7}{7}\right):\frac{4}{5}$

= $\left(-1+1\right):\frac{4}{5}$

= $0:\frac{4}{5}=0$.

b) $\frac{5}{9}:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac{5}{9}:\left(\frac{1}{15}-\frac{2}{3}\right)$

= $\frac{5}{9}:\left(\frac{2}{22}-\frac{5}{22}\right)+\frac{5}{9}:\left(\frac{1}{15}-\frac{10}{15}\right)$

= $\frac{5}{9}:\frac{-3}{22}+\frac{5}{9}:\frac{-9}{15}$

= $\frac{5}{9}.\frac{22}{-3}+\frac{5}{9}.\frac{15}{-9}$

= $\frac{5}{9}.\left(\frac{-22}{3}+\frac{-15}{9}\right)$

= $\frac{5}{9}.\left(\frac{-22}{3}+\frac{-5}{3}\right)$

= $\frac{5}{9}.\frac{-27}{3}$

= $\frac{5}{9}.\left(-9\right)=\left(-5\right)$.

Bài 11. Tìm x:

a) $\frac{3}{4}-x=4\frac{2}{3}$;

b) $\frac{2}{7}:x=\frac{1}{4}:0,125$;

c) $-\frac{7}{15}.x=7\frac{1}{3}-\frac{1}{5}$

Hướng dẫn giải

a) $\frac{3}{4}-x=4\frac{2}{3}$

$\frac{3}{4}-x=\frac{14}{3}$

$x=\frac{3}{4}-\frac{14}{3}$

$x=\frac{9}{12}-\frac{56}{12}$

$x=\frac{-47}{12}$

Vậy $x=\frac{-47}{12}$;

b) $\frac{2}{7}:x=\frac{1}{4}:0,125$

$\frac{2}{7}:x=\frac{1}{4}:\frac{1}{8}$

$\frac{2}{7}:x=\frac{1}{4}.\frac{8}{1}$

$\frac{2}{7}:x=2$

$x=\frac{2}{7}:2$

$x=\frac{1}{7}$

Vậy $x=\frac{1}{7}$.

c) $-\frac{7}{15}.x=7\frac{1}{3}-\frac{1}{5}$

$-\frac{7}{15}.x=\frac{22}{3}-\frac{1}{5}$

$-\frac{7}{15}.x=\frac{110}{15}-\frac{3}{15}$

$-\frac{7}{15}.x=\frac{107}{15}$

$x=\frac{107}{15}:\left(-\frac{7}{15}\right)$

$x=\frac{107}{15}.\left(-\frac{15}{7}\right)$

$x=-\frac{107}{7}$

Vậy $x=-\frac{107}{7}$;

Bài 12. Một đội công nhân ngày thứ nhất sửa được $\frac{4}{15}$ quãng đường, ngày thứ hai sửa được $\frac{7}{30}$ quãng đường, ngày thứ ba sửa được $\frac{3}{10}$ quãng đường. Hỏi đội công nhân còn phải sửa bao nhiêu phần của quãng đường nữa?

Hướng dẫn giải

Đội công nhân đã sửa được số phần quãng đường là:

$\frac{4}{15}+\frac{7}{30}+\frac{3}{10}=\frac{4}{5}$ (quãng đường)

Đội công nhân còn phải sửa số phần quãng đường là:

$1-\frac{4}{5}=\frac{1}{5}$ (quãng đường)

Vậy đội công nhân còn phải sửa $\frac{1}{5}$ quãng đường.

Bài 13. Một khu đất hình chữ nhật có chiều dài bằng 34,6 m, chiều rộng bằng $\frac{3}{4}$ chiều dài. Tính chu vi và diện tích của khu đất đó.

Hướng dẫn giải

Chiều rộng khu đấthình chữ nhật là:

$34,6.\frac{3}{4}=25,95$ (m)

Chu vi khu đất hình chữ nhật là:

(34,6 + 25,95). 2 = 121,1 (m)

Diện tích khu đất hình chữ nhật là:

34,6 . 25,95 = 897,87 (m²)

Vậy chu vi và diện tích của khu đất lần lượt là 121,1 m và 897,87 m².

Bài 14. Một cửa hàng có 45 tạ gạo. Ngày thứ nhất bán được $\frac{3}{4}$ số gạo, ngày thứ hai bán được $\frac{4}{5}$ số gạo còn lại. Hỏi sau hai ngày cửa hàng còn lại bao nhiêu tạ gạo?

Hướng dẫn giải

Ngày thứ nhất cửa hàng bán được số gạo là:

$45.\frac{3}{4}=33,75$ (tạ)

Sau ngày thứ nhất cửa hàng còn lại số gạo là:

45 – 33,75 = 11,25 (tạ)

Ngày thứ hai cửa hàng bán được số gạo là:

$11,25.\frac{4}{5}=9$ (tạ)

Sau hai ngày cửa hàng còn lại số gạo là:

45 – 33,75 – 9 = 2,25 (tạ)

Vậy sau hai ngày cửa hàng còn lại 2,25 tạ.

Bài 15. Viết các số sau dưới dạng luỹ thừa số mũ lớn hơn 1:

$0,36;\frac{1}{9};\frac{-27}{216};\frac{144}{225}$.

Hướng dẫn giải

Ta có 0,36 = 0,6 . 0,6 = (0,6)²;

$\frac{1}{9}=\frac{1}{3}.\frac{1}{3}={\left(\frac{1}{3}\right)}^2$;

$\frac{-27}{216}=\frac{-3}{6}.\frac{-3}{6}.\frac{-3}{6}={\left(\frac{-3}{6}\right)}^3$;

$\frac{144}{225}=\frac{12}{15}.\frac{12}{15}={\left(\frac{12}{15}\right)}^2$.

Bài 16. Tính:

${\left(-\frac{1}{2}\right)}^2;{\left(-\frac{1}{2}\right)}^3;{\left(-\frac{1}{2}\right)}^4;{\left(-\frac{1}{2}\right)}^5$

Hãy rút ra nhận xét về dấu của luỹ thừa với số mũ chẵn và luỹ thừa với số mũ lẻ của một số hữu tỉ âm.

Hướng dẫn giải

Ta có:

${\left(-\frac{1}{2}\right)}^2=\frac{{\left(-1\right)}^2}{2^2}=\frac{1}{4}$;

${\left(-\frac{1}{2}\right)}^3=\frac{{\left(-1\right)}^3}{2^3}=\frac{-1}{8}$;

${\left(-\frac{1}{2}\right)}^4=\frac{{\left(-1\right)}^4}{2^4}=\frac{1}{16}$;

${\left(-\frac{1}{2}\right)}^5=\frac{{\left(-1\right)}^5}{2^5}=\frac{-1}{32}$.

Nhận xét:

– Lũy thừa với số mũ chẵn của một số hữu tỉ âm là một số hữu tỉ dương.

– Lũy thừa với số mũ lẻ của một số hữu tỉ âm là một số hữu tỉ âm.

Bài 17. Tìm x:

a) $x:{\left(\frac{3}{4}\right)}^2=\frac{3}{4}$ ;

b) $x.{\left(\frac{-2}{5}\right)}^7={\left(\frac{-2}{5}\right)}^9$;

c) $x:{\left(0,5\right)}^6={\left(\frac{1}{2}\right)}^9$ .

Hướng dẫn giải

a) $x:{\left(\frac{3}{4}\right)}^2=\frac{3}{4}$

$x=\frac{3}{4}.{\left(\frac{3}{4}\right)}^2$

$x={\left(\frac{3}{4}\right)}^3$

$x=\frac{3^3}{4^3}$

$x=\frac{27}{64}$

Vậy $x=\frac{27}{64}$.

b) $x.{\left(\frac{-2}{5}\right)}^7={\left(\frac{-2}{5}\right)}^9$

$x={\left(\frac{-2}{5}\right)}^9:{\left(\frac{-2}{5}\right)}^7$

$x={\left(\frac{-2}{5}\right)}^{9-7}$

$x={\left(\frac{-2}{5}\right)}^2$

$x=\frac{{\left(-2\right)}^2}{5^2}$

$x=\frac{4}{25}$

Vậy $x=\frac{4}{25}$.

c) $x:{\left(0,5\right)}^3={\left(\frac{1}{2}\right)}^2$

$x:{\left(\frac{1}{2}\right)}^3={\left(\frac{1}{2}\right)}^2$

$x={\left(\frac{1}{2}\right)}^3.{\left(\frac{1}{2}\right)}^2$

$x={\left(\frac{1}{2}\right)}^5$

$x=\frac{1^5}{2^5}$

$x=\frac{1}{32}$

Vậy $x=\frac{1}{32}$.

Bài 18. Tính:

a) $\left(1+\frac{2}{3}-\frac{1}{4}\right).{\left(\frac{4}{5}-\frac{3}{4}\right)}^2$

b) $3-{\left(-\frac{6}{7}\right)}^0+{\left(\frac{1}{2}\right)}^2:2$

c) $\left({\left(\frac{2}{3}\right)}^4.{\left(\frac{2}{3}\right)}^5\right):{\left(\frac{2}{3}\right)}^6$

Hướng dẫn giải

a) $\left(1+\frac{2}{3}-\frac{1}{4}\right).{\left(\frac{4}{5}-\frac{3}{4}\right)}^2$

= $\left(\frac{1}{1}+\frac{2}{3}-\frac{1}{4}\right).{\left(\frac{16}{20}-\frac{15}{20}\right)}^2$

= $\left(\frac{12}{12}+\frac{84}{12}-\frac{3}{12}\right).{\left(\frac{1}{20}\right)}^2$

= $\left(\frac{12}{12}+\frac{8}{12}-\frac{3}{12}\right).\frac{1^2}{{20}^2}$

= $\frac{17}{12}.\frac{1}{400}=\frac{17}{4800}$;

b) $3-{\left(-\frac{6}{7}\right)}^0+{\left(\frac{1}{2}\right)}^2:2$

= $3-1+\frac{1^2}{2^2}:2$

= $3-1+\frac{1}{4}:2$

= $3-1+\frac{1}{4}.\frac{1}{2}$

= $3-1+\frac{1}{8}$

= $2+\frac{1}{8}=\frac{2}{1}+\frac{1}{8}$

= $\frac{16}{8}+\frac{1}{8}=\frac{17}{8}$;

c) $\left({\left(\frac{2}{3}\right)}^4.{\left(\frac{2}{3}\right)}^5\right):{\left(\frac{2}{3}\right)}^6$

= ${\left(\frac{2}{3}\right)}^{4+5}:{\left(\frac{2}{3}\right)}^6$

= ${\left(\frac{2}{3}\right)}^9:{\left(\frac{2}{3}\right)}^6$

= ${\left(\frac{2}{3}\right)}^{9-6}$

= ${\left(\frac{2}{3}\right)}^3=\frac{2^3}{3^3}=\frac{8}{27}$;

Bài 19. Bỏ dấu ngoặc rồi tính:

a) $\left(\frac{-2}{3}\right)+\left(\frac{4}{5}-\frac{1}{2}\right)$

b) $\frac{6}{7}-\left(\frac{5}{9}+\frac{4}{7}\right)$

c) $\left(\frac{-1}{4}+1\right)-\left(\frac{3}{4}-\frac{1}{6}\right)$

Hướng dẫn giải

a) $\left(\frac{-2}{3}\right)+\left(\frac{4}{5}-\frac{1}{2}\right)$

= $\left(\frac{-2}{3}\right)+\frac{4}{5}-\frac{1}{2}$

= $\frac{-20}{30}+\frac{24}{30}-\frac{15}{30}$

= $\frac{-11}{30}$;

b) $\frac{6}{7}-\left(\frac{5}{9}+\frac{4}{7}\right)$

= $\frac{6}{7}-\frac{5}{9}-\frac{4}{7}$

= $\frac{6}{7}-\frac{4}{7}-\frac{5}{9}$

= $\frac{2}{7}-\frac{5}{9}$

= $\frac{18}{63}-\frac{35}{63}=\frac{-17}{63}$;

c) $\left(\frac{-1}{4}+1\right)-\left(\frac{3}{4}-\frac{1}{6}\right)$

= $\frac{-1}{4}+1-\frac{3}{4}+\frac{1}{6}$

= $\frac{-1}{4}-\frac{3}{4}+1+\frac{1}{6}$

= $\frac{-4}{4}+1+\frac{1}{6}$

= $(-1)+1+\frac{1}{6}$

= $0+\frac{1}{6}=\frac{1}{6}$.

Bài 20. Tìm x, biết:

a) $\frac{4}{5}+x=\frac{6}{7}$;

b) $5\frac{1}{3}:\left(\frac{5}{4}-x\right)=0,8$;

c) $\frac{3}{10}x-2\frac{1}{3}=\frac{-2}{5}:\frac{2}{15}$.

Hướng dẫn giải

a) $\frac{4}{5}+x=\frac{6}{7}$

$x=\frac{6}{7}-\frac{4}{5}$

$x=\frac{30}{35}-\frac{28}{35}$

$x=\frac{2}{35}$

Vậy $x=\frac{2}{35}$.

b) $5\frac{1}{3}:\left(\frac{5}{4}-x\right)=0,8$

$\frac{16}{3}:\left(\frac{5}{4}-x\right)=\frac{4}{5}$

$\frac{5}{4}-x=\frac{16}{3}:\frac{4}{5}$

$\frac{5}{4}-x=\frac{16}{3}.\frac{5}{4}$

$\frac{5}{4}-x=\frac{20}{3}$

$x=\frac{5}{4}-\frac{20}{3}$

$x=\frac{15}{12}-\frac{80}{12}$

$x=\frac{-65}{12}$.

Vậy $x=\frac{-65}{12}$.

c) $\frac{3}{10}x-2\frac{1}{3}=\frac{-2}{5}:\frac{2}{15}$

$\frac{3}{10}x-\frac{7}{3}=\frac{-2}{5}.\frac{15}{2}$

$\frac{3}{10}x-\frac{7}{3}=-3$

$\frac{3}{10}x=-3+\frac{7}{3}$

$\frac{3}{10}x=\frac{-2}{3}$

$x=\frac{-2}{3}:\frac{3}{10}$

$x=\frac{-2}{3}.\frac{10}{3}$

$x=\frac{-20}{9}$.

Vậy $x=\frac{-20}{9}$.

Bài 21. Tính nhanh:

a) $\frac{16}{25}.\frac{3}{4}+\frac{9}{25}.\frac{3}{4}$;

b) $\frac{5}{8}.\frac{24}{13}-\frac{11}{13}.\frac{5}{8}+\frac{5}{8}$;

Hướng dẫn giải

a) $\frac{16}{25}.\frac{3}{4}+\frac{9}{25}.\frac{3}{4}$

= $\left(\frac{16}{25}+\frac{9}{25}\right).\frac{3}{4}$

= $1.\frac{3}{4}=\frac{3}{4}$;

b) $\frac{5}{8}.\frac{24}{13}-\frac{11}{13}.\frac{5}{8}+\frac{5}{8}$

= $\frac{5}{8}.\left(\frac{24}{13}-\frac{11}{13}+1\right)$

= $\frac{5}{8}.\left(\frac{13}{13}+1\right)$

= $\frac{5}{8}.\left(1+1\right)$

= $\frac{5}{8}.2=\frac{5}{4}$.

Học tốt Toán 7 Chương 1

Các bài học để học tốt Chương 1 Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài tập cuối chương 1

• Giải sbt Toán 7 Bài tập cuối chương 1