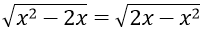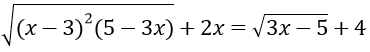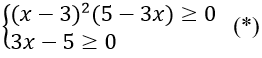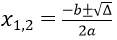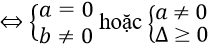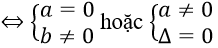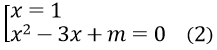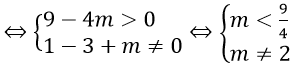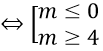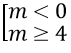Các dạng bài tập chương Phương trình, Hệ phương trình cực hay, có đáp án - Toán lớp 10

---

Các dạng bài tập chương Phương trình, Hệ phương trình cực hay, có đáp án

Với Các dạng bài tập chương Phương trình, Hệ phương trình cực hay, có đáp án Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập chương Phương trình, Hệ phương trình từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

• Dạng 1: Tìm tập xác định của phương trình Xem chi tiết
• Bài tập tìm tập xác định của phương trình Xem chi tiết
• Dạng 2: Giải phương trình bằng phương pháp biến đổi tương đương Xem chi tiết
• Bài tập giải phương trình bằng phương pháp biến đổi tương đương Xem chi tiết
• Dạng 3: Giải và biện luận phương trình bậc nhất Xem chi tiết
• Bài tập giải và biện luận phương trình bậc nhất Xem chi tiết
• Dạng 4: Giải và biện luận phương trình bậc hai Xem chi tiết
• Bài tập giải và biện luận phương trình bậc hai Xem chi tiết
• Dạng 5: Nghiệm của phương trình bậc hai Xem chi tiết
• Bài tập về nghiệm của phương trình bậc hai Xem chi tiết
• Dạng 6: Phương trình chứa ẩn trong dấu giá trị tuyệt đối Xem chi tiết
• Bài tập phương trình chứa ẩn trong dấu giá trị tuyệt đối Xem chi tiết
• Dạng 7: Phương trình chứa ẩn ở mẫu Xem chi tiết
• Bài tập phương trình chứa ẩn ở mẫu Xem chi tiết
• Dạng 8: Phương trình chứa ẩn dưới dấu căn Xem chi tiết
• Bài tập phương trình chứa ẩn dưới dấu căn Xem chi tiết
• Dạng 9: Các dạng phương trình quy về phương trình bậc hai Xem chi tiết
• Bài tập phương trình quy về phương trình bậc hai Xem chi tiết
• Dạng 10: Giải và biện luận hệ phương trình bậc nhất Xem chi tiết
• Bài tập giải và biện luận hệ phương trình bậc nhất Xem chi tiết
• Dạng 11: Các dạng hệ phương trình đặc biệt Xem chi tiết
• Bài tập các dạng hệ phương trình đặc biệt Xem chi tiết

Cách giải phương trình bằng phương pháp biến đổi tương đương

Lý thuyết & Phương pháp giải

- Phương trình tương đương: Hai phương trình f₁(x) = g₁(x) và f₂(x) = g₂(x) được gọi là tương đương nếu chúng có cùng tập nghiệm

- Kí hiệu là f₁(x) = g₁(x) ⇔ f₂(x) = g₂(x)

- Phép biến đổi không làm thay đổi tập nghiệm của phương trình gọi là phép biến đổi tương đương.

- Phương trình hệ quả: f₂(x) = g₂(x) gọi là phương trình hệ quả của phương trình f₁(x) = g₁(x) nếu tập nghiệm của nó chứa tập nghiệm của phương trình f₁(x) = g₁(x)

- Kí hiệu là f₁(x) = g₁(x) ⇒ f₂(x) = g₂(x)

- Để giải phương trình ta thực hiện các phép biến đổi để đưa về phương trình tương đương với phương trình đã cho đơn giản hơn trong việc giải nó. Một số phép biến đổi thường sử dụng:

   + Cộng (trừ) cả hai vế của phương trình mà không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương phương trình đã cho.

   + Nhân (chia) vào hai vế với một biểu thức khác không và không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương với phương trình đã cho.

   + Bình phương hai vế của phương trình ta thu được phương trình hệ quả của phương trình đã cho.

Bình phương hai vế của phương trình (hai vế luôn cùng dấu) ta thu được phương trình tương đương với phương trình đã cho.

Ví dụ minh họa

Bài 1: Giải phương trình

Hướng dẫn:

Điều kiện:

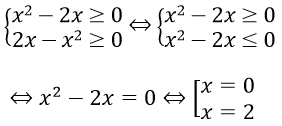
Thử lại ta thấy cả x = 0 và x = 2 đều thỏa mãn phương trình

Vậy tập nghiệm của phương trình là S = {0;2}

Bài 2: Giải phương trình

Hướng dẫn:

Điều kiện:

Ta thấy x = 3 thỏa mãn điều kiện (*)

Nếu x ≠ 3. thì (*)

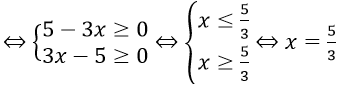
Do đó điều kiện xác định của phương trình là x = 3 hoặc x = 5/3

Thay x = 3 và x = 5/3 vào phương trình thấy chỉ có x = 3 thỏa mãn

Vậy phương trình đã cho có nghiệm duy nhất S = {3}

Bài 3: Giải phương trình

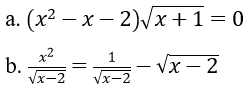
Hướng dẫn:

a. Điều kiện: x ≥ -1.

Ta có x = -1 là một nghiệm.

Nếu x > -1 thì √(x+1) > 0. Do đó phương trình tương đương

x² - x - 2 = 0 ⇔ x = -1 hoặc x = 2.

Đối chiếu điều kiện ta được nghiệm của phương trình là x = -1, x = 2.

Vậy phương trình đã cho có hai nghiệm S = {-1; 2}

b. ĐKXĐ: x > 2

Với điều kiện đó phương trình tương đương với phương trình

x² = 1 - (x - 2)⇔ x² + x - 3 = 0

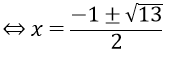
Đối chiếu với điều kiện ta thấy không có giá trị nào thỏa mãn

Vậy phương trình vô nghiệm

Cách giải và biện luận phương trình bậc nhất

Lý thuyết & Phương pháp giải

Cách giải và biện luận phương trình dạng ax+b=0 được tóm tắt trong bảng sau

ax + b = 0  (1)
Hệ số		Kết luận
a ≠ 0		(1) có nghiệm duy nhất x = -b/a
a = 0	b ≠ 0	(1) vô nghiệm
	b = 0	(1) nghiệm đúng với mọi x

Khi a ≠ 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn

Ví dụ minh họa

Bài 1: Cho phương trình (m² - 7m + 6)x + m² - 1 = 0

a. Giải phương trình khi m = 0

b. Biện luận theo m số nghiệm của phương trình

Hướng dẫn:

a. Với m = 0 phương trình trở thành 6x - 1 = 0 ⇔ x = 1/6

Phương trình có nghiệm duy nhất x = 1/6

b. Ta có (m² - 7m + 6)x + m² - 1 = 0 ⇔ (m-1)(m-6)x + (m-1)(m+1) = 0

Nếu (m-1)(m-6) ≠ 0 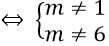thì phương trình có nghiệm duy nhất x = -(m+1)/(m-6)

Nếu m = 1 phương trình trở thành 0 = 0. Khi đó phương trình có vô số nghiệm.

Nếu m = 6 thì phương trình trở thành 35 = 0 (Vô lí). Khi đó phương trình vô nghiệm.

Bài 2: Tìm tất cả các giá trị thực của tham số m để phương trình (2m - 4)x = m - 2 có nghiệm duy nhất.

Hướng dẫn:

Phương trình đã cho có nghiệm duy nhất khi 2m - 4 ≠ 0 ⇔ m ≠ 2

Bài 3: Tìm tất cả các giá trị thực của tham số m để phương trình (m² - 5m + 6)x = m² - 2m vô nghiệm.

Hướng dẫn:

Phương trình đã cho vô nghiệm khi

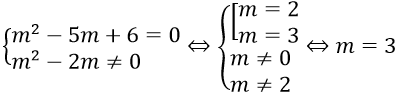
Phương pháp giải và biện luận phương trình bậc hai

Lý thuyết & Phương pháp giải

Giải và biện luận phương trình bậc hai ax² + bx + c = 0

Bước 1. Biến đổi phương trình về đúng dạng ax² + bx + c = 0

Bước 2. Nếu hệ số a chứa tham số, ta xét 2 trường hợp:

   - Trường hợp 1: a = 0, ta giải và biện luận ax + b = 0.

   - Trường hợp 2: a ≠ 0. Ta lập Δ = b² - 4ac. Khi đó:

      + Nếu Δ > 0 thì phương trình có 2 nghiệm phân biệt

      + Nếu Δ = 0 thì phương trình có 1 nghiệm (kép): x = -b/2a

      + Nếu Δ < 0 thì phương trình vô nghiệm.

Bước 3. Kết luận.

Lưu ý:

- Phương trình ax² + bx + c = 0 có nghiệm

- Phương trình ax² + bx + c = 0 có nghiệm duy nhất

Ví dụ minh họa

Bài 1: Phương trình (m–1)x² + 3x – 1 = 0. Phương trình có nghiệm khi:

Hướng dẫn:

Với m = 1, phương trình trở thành 3x - 1 = 0 ⇔ x = 1/3

Do đó m = 1 thỏa mãn.

Với m ≠ 1, ta có Δ = 9 + 4(m-1) = 4m + 5

Phương trình có nghiệm khi Δ ≥ 0

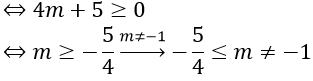
Hợp hai trường hợp ta được m ≥ -5/4 là giá trị cần tìm

Bài 2: Phương trình (x² - 3x + m)(x - 1) = 0 có 3 nghiệm phân biệt khi:

Hướng dẫn:

Phương trình (x² - 3x + m)(x - 1) = 0 ⇔

Phương trình (1) có 3 nghiệm phân biệt

⇔ Phương trình (2) có hai nghiệm phân biệt khác 1

Bài 3: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để phương trình mx² - mx + 1 = 0 có nghiệm.

Hướng dẫn:

Nếu m = 0 thì phương trình trở thành 1 = 0: vô nghiệm.

Khi m ≠ 0, phương trình đã cho có nghiệm khi và chỉ khi

Δ = m² - 4m ≥ 0

Kết hợp điều kiện m ≠ 0, ta được

Vì ∈ Z, m ∈ [-10;10] m ∈ {-10; -9; -8;...; -1} ∪ {4; 5; 6;...; 10}

Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán