Giả sử un là số hạng thứ n của dãy số (un)
Giả sử u là số hạng thứ n của dãy số (u) và .
Giải sách bài tập Toán 11 Bài tập ôn tập cuối năm - Kết nối tri thức
Bài 29 trang 70 SBT Toán 11 Tập 2: Giả sử un là số hạng thứ n của dãy số (un) và .
a) Chứng tỏ rằng u1 = 1, u2 = 1 và un + 2 = un + 1 + un với mọi n ℕ*. Từ đó suy ra (un) là dãy số Fibonacci.
b) Viết 11 số hạng đầu tiên của dãy Fibonacci và 10 tỉ số đầu tiên.
Tính .
Lời giải:
a) Ta có an + 2 – bn + 2 = an + 1.a − bn + 1.b
= an + 1.a + an + 1.b − bn + 1.b − bn + 1.a − an + 1.b + bn + 1.a
= an + 1.(a + b) − bn + 1.(a + b) – ab(an − bn)
= (an + 1 − bn + 1).(a + b) – ab(an − bn) (*)
Có .
.
Áp dụng (*), ta có:
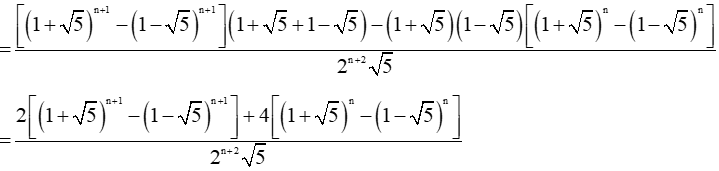
= un+1 + un.
Vậy un + 2 = un+1 + un. Do đó (un) là dãy Fibonacci.
b) Ta có bảng sau
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
un |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
Ta có
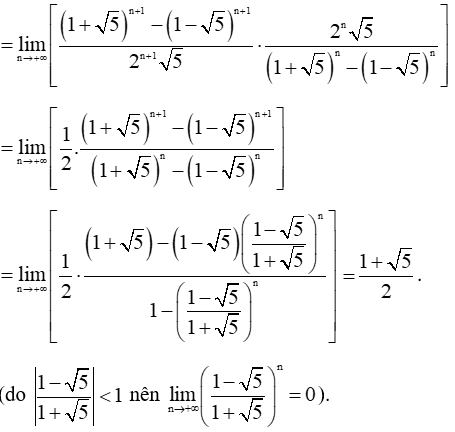
Lời giải SBT Toán 11 Bài tập ôn tập cuối năm hay khác:
Bài 13 trang 68 SBT Toán 11 Tập 2: Cho mẫu số liệu ghép nhóm sau về thời gian sử dụng mạng xã hội của một nhóm học sinh trong ngày ....
Bài 14 trang 68 SBT Toán 11 Tập 2: Cho mẫu số liệu ghép nhóm sau về thời gian sử dụng mạng xã hội của một nhóm học sinh trong ngày ....
Bài 15 trang 68 SBT Toán 11 Tập 2: Trong tỉnh X, tỉ lệ học sinh học giỏi môn Ngữ văn là 9%, học giỏi môn Toán là 12% và học giỏi cả hai môn là 7% ....
Bài 16 trang 68 SBT Toán 11 Tập 2: Có hai hộp đựng bi. Hộp I có 3 viên bi xanh và 2 viên bi đỏ. Hộp 2 có 5 viên bi xanh và 1 viên bi đỏ ....
Bài 17 trang 68 SBT Toán 11 Tập 2: Có bốn đồng xu I, II, III và IV. Xác suất xuất hiện mặt ngửa khi gieo đồng xu I và II là . Xác suất xuất hiện mặt ngửa khi gieo đồng xu III và IV là ....
Bài 18 trang 69 SBT Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau, giao tuyến của (P) và (Q) là đường thẳng c. Gọi a là đường thẳng nằm trên (P) và vuông góc với đường thẳng c, b ....
Bài 19 trang 69 SBT Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Góc giữa hai đường thẳng AC và BC' bằng ....
Bài 20 trang 69 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có mặt phẳng (SAB) vuông góc với mặt đáy (ABCD), tam giác SAB đều, đáy ABCD là hình vuông cạnh bằng a ....
Bài 21 trang 69 SBT Toán 11 Tập 2: Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA bằng a . Khoảng cách giữa hai đường thẳng BD và SC là ....
Bài 22 trang 69 SBT Toán 11 Tập 2: Cho hình lăng trụ ABC.A'B'C' có AA'B'C' là hình tứ diện đều cạnh bằng a. Tính thể tích khối lăng trụ ABC.A'B'C' bằng ....
Bài 23 trang 69 SBT Toán 11 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = a, AA' = a . Thể tích khối tứ diện ACB'D' bằng ....
Bài 24 trang 69 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a và SA vuông góc với mặt phẳng (ABC). Khoảng cách giữa hai đường thẳng SA và BC bằng ....
Bài 25 trang 70 SBT Toán 11 Tập 2: Cho sinx = -, x . Tính giá trị cos ....
Bài 26 trang 70 SBT Toán 11 Tập 2: Chứng minh rằng: a) sin3x = 4sinx sin(60° − x) sin(60° + x) ....
Bài 27 trang 70 SBT Toán 11 Tập 2: Xét xem các dãy số với công thức tổng quát sau có phải là cấp số cộng/cấp số nhân hay không ....
Bài 28 trang 70 SBT Toán 11 Tập 2: Một công ty kĩ thuật đưa ra hai phương án về lương cho kĩ sư làm việc tại công ty như sau ....
Bài 30 trang 70 SBT Toán 11 Tập 2: Tính các giới hạn sau: a) ; b) ....
Bài 31 trang 71 SBT Toán 11 Tập 2: Tìm m để hàm số sau liên tục trên toàn bộ tập số thực ℝ ....
Bài 32 trang 71 SBT Toán 11 Tập 2: Giải các phương trình sau: a) ....
Bài 33 trang 71 SBT Toán 11 Tập 2: Cho các hàm số f(x) = 32x −1 và g(x) = xln9. Giải bất phương trình f'(x) < g'(x) ....
Bài 34 trang 71 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau: a) ....
Bài 35 trang 71 SBT Toán 11 Tập 2: Tiếp tuyến của đồ thị hàm số y = 2x3 – 3x2 – 11x + 13 tại điểm M có hệ số góc là 1. Tìm tọa độ điểm M ....
Bài 36 trang 71 SBT Toán 11 Tập 2: Cho phương trình dao động x(t) = 10cos, ở đây li độ x tính bằng centimét và thời gian t tính bằng giây ....
Bài 37 trang 71 SBT Toán 11 Tập 2: Một công ty bất động sản đã thống kê số lượng khách hàng theo giá đất họ đầu tư và thu được kết quả như sau ....
Bài 38 trang 71 SBT Toán 11 Tập 2: Gieo hai con xúc xắc I và II cân đối, đồng chất một cách độc lập. Xét các biến cố A, B sau đây ....
Bài 39 trang 72 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, đường thẳng SA vuông góc với mặt phẳng (ABCD) và SA = a ....
Bài 40 trang 72 SBT Toán 11 Tập 2: Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA = a ....
Bài 41 trang 72 SBT Toán 11 Tập 2: Cho hình lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a, tam giác AB'C' cân tại A ....
Bài 42 trang 72 SBT Toán 11 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a; AD = a, góc giữa đường thẳng A'C và mặt phẳng (ABCD) bằng 30° ....
Bài 43 trang 72 SBT Toán 11 Tập 2: Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = a, AA' = 2a. Gọi M, N lần lượt là trung điểm của các cạnh BB' và CC' ....
liên tục trên ℝ là ....

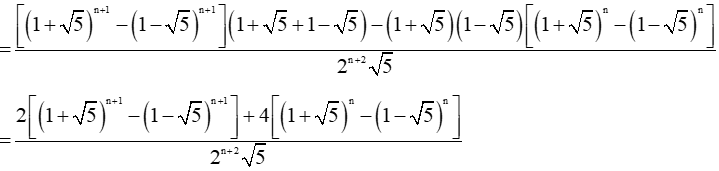
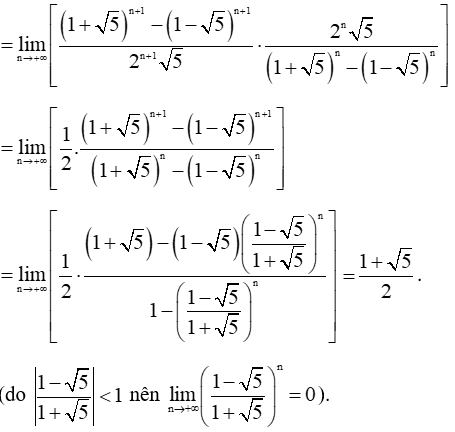
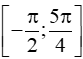 là ....
là ....