Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau y = (-x^3/3) − x^2 + 3x + 1 trên khoảng (0; 3)

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau:

Giải SBT Toán 12 Cánh diều Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 41 trang 19 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau:

a) y = $\frac{- x^{3}}{3}$ − x² + 3x + 1 trên khoảng (0; 3);

b) y = x⁴ – 8x² + 10 trên khoảng ( $- \sqrt{7}$ ; $\sqrt{7}$ );

c) $y = \frac{x^{2} - 1}{x^{2} + 1}$ ;

d) y = x + $\frac{4}{x - 1}$ trên khoảng (−∞; 1).

Lời giải:

a) y = $\frac{- x^{3}}{3}$ − x² + 3x + 1 trên khoảng (0; 3)

Tập xác định: D = ℝ.

Ta có: y = $\frac{- x^{3}}{3}$ − x² + 3x + 1 ⇒y' = −x² – 2x + 3.

y' = 0 ⇔ −x² – 2x + 3 = 0 ⇔ x = 1 hoặc x = −3.

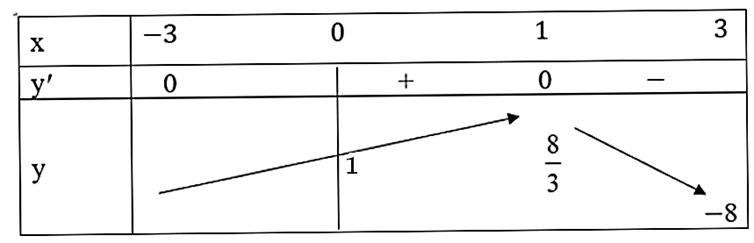
Ta có bảng biến thiên như sau:

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau y = (-x^3/3) − x^2 + 3x + 1 trên khoảng (0; 3)

Vậy $\max_{(0; 3)}$ y = $\frac{8}{3}$ tại x = 1 và hàm số không có giá trị nhỏ nhất trên khoảng (0; 3).

b) y = x⁴ – 8x² + 10 trên khoảng ( $- \sqrt{7}$ ; $\sqrt{7}$ )

Tập xác định: D = ℝ.

Ta có: y = x⁴ – 8x² + 10 ⇒y' = 4x³ – 16x.

y' = 0 ⇔ 4x³ – 16x = 0 ⇔ x = 0 hoặc x = ±2.

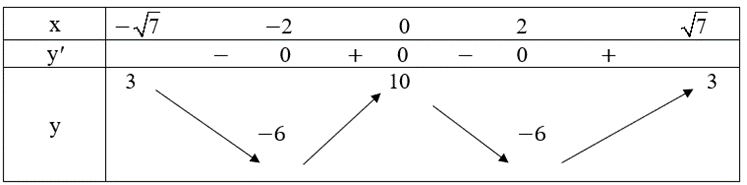
Ta có bảng biến thiên như sau:

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau y = (-x^3/3) − x^2 + 3x + 1 trên khoảng (0; 3)

Vậy $\max_{(- \sqrt{7}; \sqrt{7})}$ y = 10 tại x = 0, $\min_{(- \sqrt{7}; \sqrt{7})}$ y = − 6 tại x = −2, x = 2.

c) $y = \frac{x^{2} - 1}{x^{2} + 1}$ .

Tập xác định: D = ℝ.

Ta có: $y = \frac{x^{2} - 1}{x^{2} + 1}$ ⇒y' = $\frac{2 x (x^{2} + 1) - 2 x (x^{2} - 1)}{{(x^{2} + 1)}^{2}}$ = $\frac{4 x}{{(x^{2} + 1)}^{2}}$ .

y' = 0 ⇔ $\frac{4 x}{{(x^{2} + 1)}^{2}}$ = 0 ⇔ x = 0.

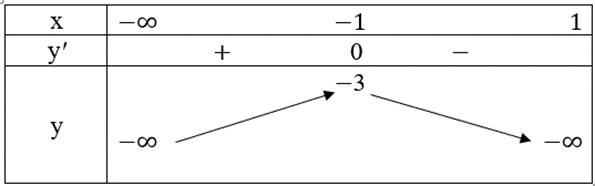
Ta có bảng xét dấu như sau:

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau y = (-x^3/3) − x^2 + 3x + 1 trên khoảng (0; 3)

Vậy $\min_{ℝ}$ y = −1 tại x = 0, hàm không có giá trị lớn nhất trên ℝ.

d) y = x + $\frac{4}{x - 1}$ trên khoảng (−∞; 1).

Tập xác định: D = ℝ\{1}.

Ta có: y = x + $\frac{4}{x - 1}$ ⇒y' = 1 − $\frac{4}{{(x - 1)}^{2}}$ .

y' = 0 ⇔ 1 − $\frac{4}{{(x - 1)}^{2}}$ = 0 ⇔ x = 3 (3 ∉ (−∞; 1)) hoặc x = −1 (−1 ∈ (−∞; 1)).

Ta có bảng biến thiên như sau:

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau y = (-x^3/3) − x^2 + 3x + 1 trên khoảng (0; 3)

Vậy $\max_{(- \infty; 1)}$ y = −3 tại x = −1, hàm số không có giá trị nhỏ nhất trên khoảng (−∞; 1).

Lời giải SBT Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay khác: