Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông

❮ Bài trước Bài sau ❯

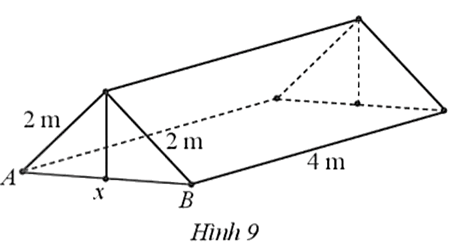
Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như với hai mép tấm bạt sát mặt đất. Tính khoảng cách AB để khoảng không gian trong lều là lớn nhất.

Giải SBT Toán 12 Cánh diều Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 45 trang 20 SBT Toán 12 Tập 1: Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như Hình 9 với hai mép tấm bạt sát mặt đất. Tính khoảng cách AB để khoảng không gian trong lều là lớn nhất.

Lời giải:

Gọi độ dài đoạn AB là x (x > 0, đơn vị: mét).

Lều có dạng hình lăng trụ đứng tam giác với chiều cao h = 4 m và tam giác đáy có độ dài các cạnh là 2 m, 2m, x m, suy ra chiều cao tam giác đáy là $\sqrt{4 - \frac{x^{2}}{4}}$ (m).

Để không gian trong lều là lớn nhất tức là thể tích của nó lớn nhất.

V = S.h = $\frac{1}{2}$ .x. $\sqrt{4 - \frac{x^{2}}{4}}$ .4 = 2x. $\sqrt{4 - \frac{x^{2}}{4}}$ = x. $\sqrt{16 - x^{2}}$ (0 < x < 4).

Ta có: x. $\sqrt{16 - x^{2}}$ ≤ $\frac{x^{2} + 16 - x^{2}}{2}$ = 18.

Dấu bằng xảy ra khi và chỉ khi x = $\sqrt{16 - x^{2}}$ ⇔ x = 2 $\sqrt{2}$ ∈ (0; 4).

Vậy V_max = 18 m³ khi AB = 2 $\sqrt{2}$ m.

Lời giải SBT Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯