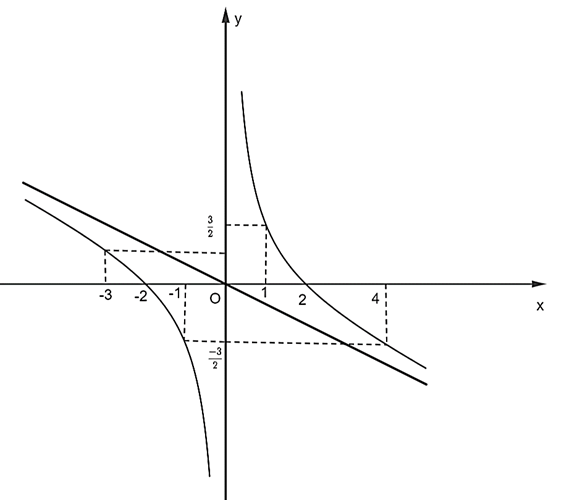Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

❮ Bài trước Bài sau ❯

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

Giải SBT Toán 12 Cánh diều Bài tập cuối chương 1

Bài 108 trang 44 SBT Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

a) y = x³ – 6x² + 9x – 2;

b) y = −x³ – x;

c) y = $\frac{2 x - 4}{x + 1}$ ;

d) $y = \frac{- x + 3}{x - 2}$ ;

e) y = $\frac{x^{2} - x + 2}{x + 1}$ ;

g) y = $\frac{- x^{2} + 4}{2 x}$ .

Lời giải:

a) y = x³ – 6x² + 9x – 2

1) Tập xác định: D = ℝ.

2) Sự biến thiên

Giới hạn tại vô cực: $\lim_{x \to + \infty}$ y = +∞, $\lim_{x \to - \infty}$ y = −∞.

Ta có: y = x³ – 6x² + 9x – 2 ⇒ y' = 3x² – 12x + 9.

y' = 0 ⇔ 3x² – 12x + 9 = 0 ⇔ x = 1 hoặc x = 3.

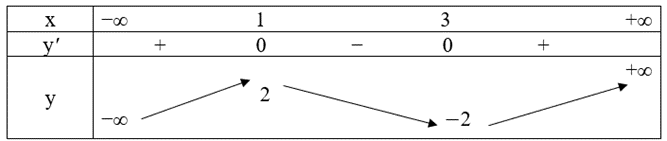
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞).

Hàm số nghịch biến trên khoảng (1; 3).

Hàm số đạt cực đại tại x = 1, y_CĐ = 2; đạt cực tiểu tại x = 3, y_CT = −2.

3) Đồ thị:

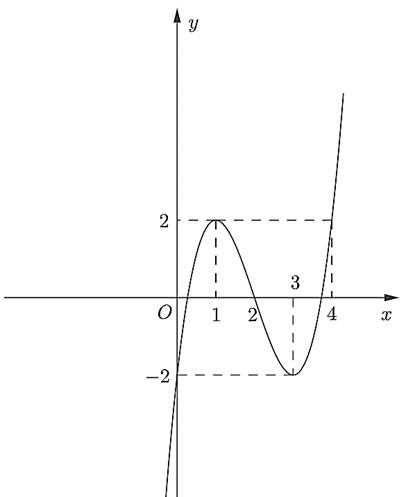
Đồ thị hàm số giao với trục tung tại điểm: (0; −2).

Đồ thị hàm số đi qua các điểm: (0; −2); (1; 2); (2; 0); (3; −2); (4; 2).

Ta có đồ thị như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

b) y = −x³ – x

1) Tập xác định: D = ℝ.

2) Sự biến thiên

Giới hạn tại vô cực: $\lim_{x \to + \infty}$ y = −∞, $\lim_{x \to - \infty}$ y = +∞.

Ta có: y = −x³ – x

⇒ y' = −3x² – 1 < 0 với mọi x.

Hàm số nghịch biến trên ℝ.

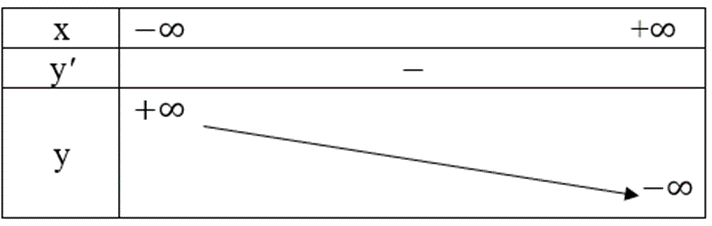
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Hàm số không có cực trị.

3) Đồ thị

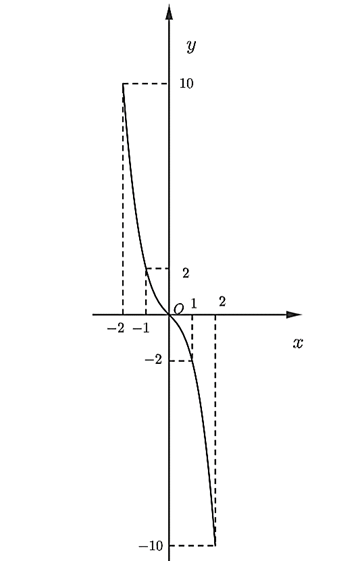
Đồ thị hàm số đi qua các điểm: (−2; 10); (−1; 2); (0; 0); (1; −2); (2; −10).

Có đồ thị hàm số như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

c) y = $\frac{2 x - 4}{x + 1}$

1) Tập xác định: D = ℝ\{−1}.

2) Sự biến thiên

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

Ta có: $\lim_{x \to + \infty}$ y = 2, $\lim_{x \to - \infty}$ y = 2.

Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

$\lim_{x \to - 1^{-}}$ y = +∞, $\lim_{x \to - 1^{+}}$ y = −∞.

Do đó, đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.

y' = $\frac{6}{{(x + 1)}^{2}}$ > 0, với ∀x ∈ D.

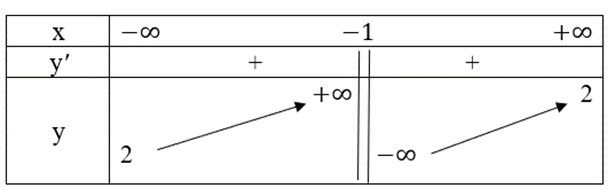
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞).

3) Đồ thị

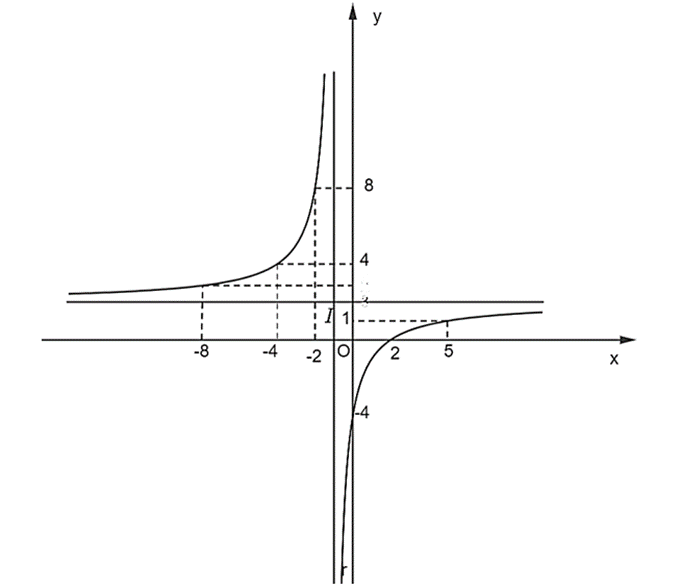
Đồ thị hàm số nhận đường thẳng x = −1 làm tiệm cận đứng, y = 2 làm tiệm cận ngang.

Đồ thị hàm số đi qua các điểm (0; −4); (2; 0); (1; −1); (−2; 8); (5; 1); (−4; 4); $(- 8; \frac{20}{7})$ .

Có đồ thị hàm số như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (−1; 2) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

d) $y = \frac{- x + 3}{x - 2}$

1) Tập xác định: D = ℝ\{2}.

2) Sự biến thiên

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.

Ta có: $\lim_{x \to + \infty}$ y = −1, $\lim_{x \to - \infty}$ y = −1.

Do đó, đường thẳng y = −1 là tiệm cận ngang của đồ thị hàm số.

$\lim_{x \to 2^{-}}$ y = −∞, $\lim_{x \to 2^{+}}$ y = +∞.

Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

Ta có: y' = $\frac{- 1}{{(x - 2)}^{2}}$ < 0 với ∀x ∈ D.

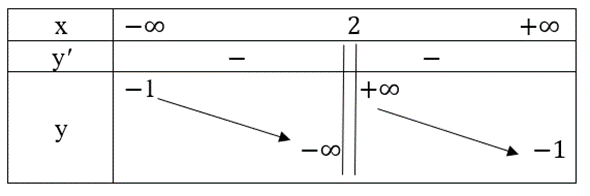
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).

3) Đồ thị

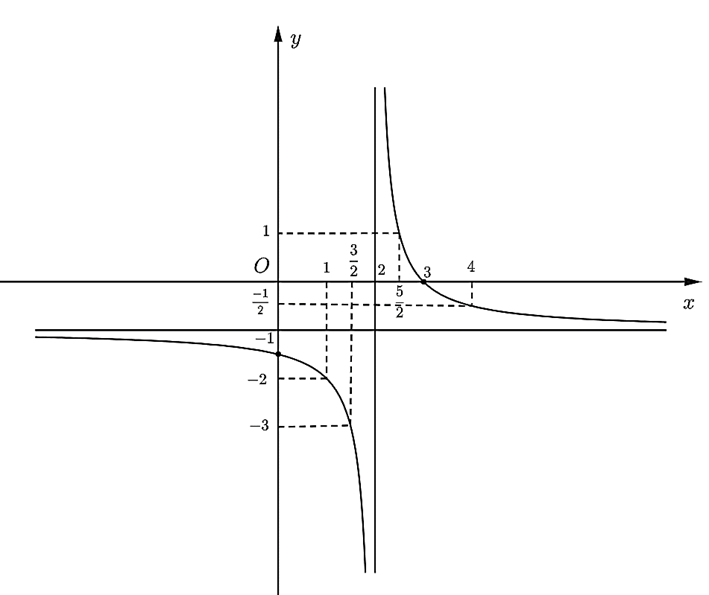
Đồ thị hàm số nhận đường thẳng x = 2 làm tiệm cận đứng, y = −1 làm tiệm cận ngang.

Đồ thị hàm số đi qua các điểm $(0; \frac{- 3}{2})$ ; (1; −2); $(\frac{3}{2}; - 3)$ ; $(\frac{5}{2}; 1)$ ; (3; 0); $(4; \frac{- 1}{2})$ .

Ta có đồ thị hàm số như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (2; −1) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

e) y = $\frac{x^{2} - x + 2}{x + 1}$

1) Tập xác định: D = ℝ\{−1}.

2) Sự biến thiên

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

Ta có: $\lim_{x \to + \infty}$ y = +∞, $\lim_{x \to - \infty}$ y = −∞.

Do đó, hàm số không có đường tiệm cận ngang.

$\lim_{x \to - 1^{-}}$ y = −∞, $\lim_{x \to - 1^{+}}$ y = +∞.

Do đó, đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.

$\lim_{x \to + \infty}$ $\frac{y}{x}$ = $\lim_{x \to + \infty}$ $\frac{x^{2} - x + 2}{(x + 1) x}$ = $\lim_{x \to + \infty}$ $\frac{x^{2} - x + 2}{x^{2} + x}$ = 1.

$\lim_{x \to + \infty}$ (y – x) = $\lim_{x \to + \infty}$ $(\frac{x^{2} - x + 2}{x + 1} - x)$ = $\lim_{x \to + \infty}$ $\frac{- 2 x + 2}{x + 1}$ = −2.

Do đó, đường thẳng y = x − 2 là tiệm cận xiên của đồ thị hàm số.

Ta có: y' = $\frac{x^{2} + 2 x - 3}{{(x + 1)}^{2}}$ ;

y' = 0 khi x = 1 hoặc x = −3.

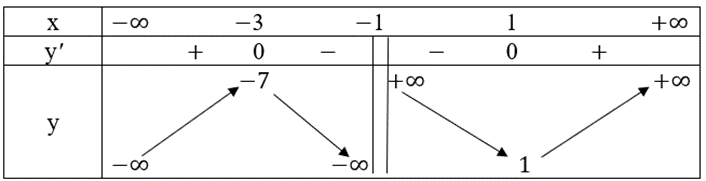
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Hàm số đồng biến trên các khoảng (−∞; −3) và (1; +∞).

Hàm số nghịch biến trên các khoảng (−3; −1) và (−1; 1).

Hàm số đạt cực đại tại x = −3, y_CĐ = −7; đạt cực tiểu tại x = 1, y_CT = 1.

3) Đồ thị

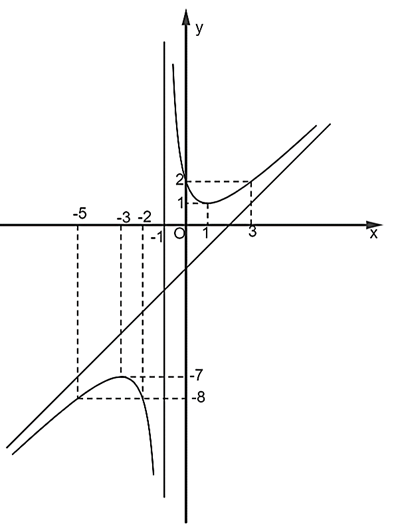
Đồ thị hàm số nhận đường thẳng x = −1 làm tiệm cận đứng, y = x – 2 làm tiệm cận xiên.

Đồ thị hàm số đi qua các điểm: (−5; −8); (−3; −7); (−2; −8); (0; 2); (1; 1); (3; 2).

Có đồ thị hàm số như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (−1; −3) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

g) y = $\frac{- x^{2} + 4}{2 x}$

1) Tập xác định: D = ℝ\{0}.

2) Sự biến thiên

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

Ta có: $\lim_{x \to + \infty}$ y = −∞, $\lim_{x \to - \infty}$ y = +∞.

Do đó, hàm số không có đường tiệm cận ngang.

$\lim_{x \to 0^{-}}$ y = −∞, $\lim_{x \to 0^{+}}$ y = +∞.

Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số.

$\lim_{x \to + \infty}$ $\frac{y}{x}$ = $\lim_{x \to + \infty}$ $\frac{- x^{2} + 4}{2 x^{2}}$ = $\frac{- 1}{2}$ .

$\lim_{x \to + \infty}$ = $\lim_{x \to + \infty}$ $(\frac{- x^{2} + 4}{2 x} + \frac{1}{2} x)$ = $\lim_{x \to + \infty}$ $\frac{2}{x}$ = 0.

Do đó, đường thẳng y = là tiệm cận xiên của đồ thị hàm số.

Ta có y' = $\frac{- 2 x^{2} - 8}{4 x^{2}}$ < 0 với ∀x ∈ D.

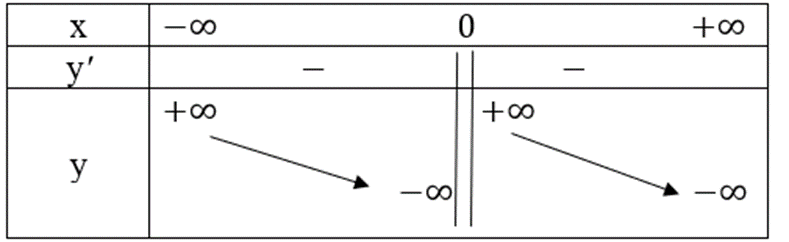
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Hàm số nghịch biến trên các khoảng (−∞; 0) và (0; +∞).

Hàm số không có cực trị.

3) Đồ thị

Đồ thị nhận được thẳng x = 0 làm tiệm cận đứng, y = $\frac{- 1}{2}$ x làm tiệm cận xiên.

Đồ thị hàm số đi qua các điểm: $(1; \frac{3}{2})$ ; $(- 1; - \frac{3}{2})$ ;(2; 0); $(- 3; \frac{5}{6})$ ; (−2; 0); $(4; \frac{- 3}{2})$ .

Có đồ thị hàm số như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = x^3 – 6x^2 + 9x – 2

Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (0; 0) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

Lời giải SBT Toán 12 Bài tập cuối chương 1 hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯