Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32

❮ Bài trước Bài sau ❯

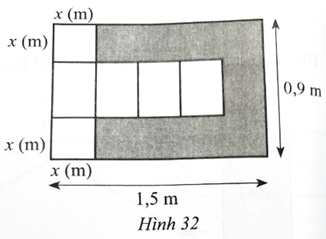
Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32. Bạn Minh cắt đi phần tô màu xám và gấp lại để được một hình hộp chữ nhật. Gọi V là thể tích hình hộp chữ nhật được tạo thành, V được tính theo x bởi công thức nào? Tìm x để hình hộp tạo thành có thể tích lớn nhất.

Giải SBT Toán 12 Cánh diều Bài tập cuối chương 1

Bài 109 trang 44 SBT Toán 12 Tập 1: Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32. Bạn Minh cắt đi phần tô màu xám và gấp lại để được một hình hộp chữ nhật. Gọi V là thể tích hình hộp chữ nhật được tạo thành, V được tính theo x bởi công thức nào? Tìm x để hình hộp tạo thành có thể tích lớn nhất.

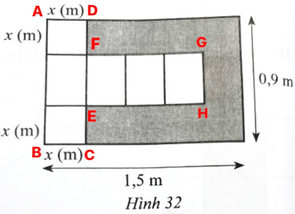
Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32

Lời giải:

Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32

Đặt các điểm trên Hình 32 như trên. Khi đó ta có:

EF = DC – DF – EC = 0,9 − 2x (m).

Lúc này, khi miếng bìa được gập vào thành hình hộp chữ nhật có chiều cao là x (m), chiều rộng đáy là x (m) và chiều dài đáy là 0,9 – 2x (m).

Suy ra V = x².(0,9 – 2x) (m³)

Xét hàm số V(x) = x².(0,9 – 2x).

V'(x) = −6x² + 1,8x

V'(x) = 0 ⇔ −6x² + 1,8x = 0 ⇔ x = 0 hoặc x = 0,3.

Mà điều kiện 0 < x < $\frac{0, 9}{2}$ = 0,45 nên x = 0,3 thỏa mãn điều kiện.

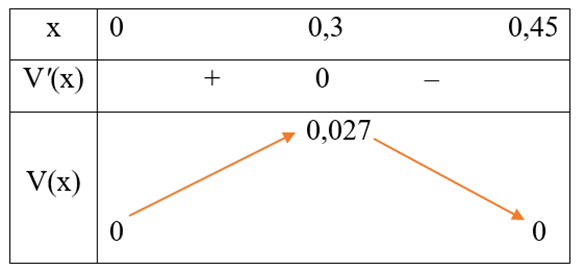
Bảng biến thiên của hàm số V(x) trên khoảng (0; 0,45) như sau:

Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32

Căn cứ vào bảng biến thiên, ta có hàm số V(x) đạt giá trị lớn nhất 0,027 tại x = 0,3.

Vậy x = 0,3 m thì thể tích của hình hộp chữ nhật tạo thành là lớn nhất.

Lời giải SBT Toán 12 Bài tập cuối chương 1 hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

2018 © All Rights Reserved.