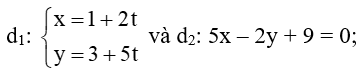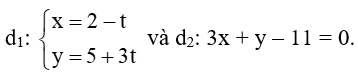Bài 4 trang 57 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10
Xét vị trí tương đối của các cặp đường thẳng d và d sau đây:
Giải Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 4 trang 57 Toán lớp 10 Tập 2: Xét vị trí tương đối của các cặp đường thẳng d1 và d2 sau đây:
a) d1: x – y + 2 = 0 và d2 : x + y + 4 = 0;
b)
c)
Lời giải:
a) Đường thẳng d1 có vectơ pháp tuyến là = (1; −1)
Đường thẳng d2 có vectơ pháp tuyến là = (1; 1).
Ta có: . = 1. 1 + 1. (−1) = 0 ⇒ ⊥.
⇒ d1 ⊥ d2.
Vậy d1 vuông góc với d2.
b) Đường thẳng d1 có VTCP là = (2; 5) ⇒ VTPT của d1 là = (5; −2).
Đường thẳng d2 có VTCP là = (5; −2).
⇒ = . Do đó, d1 và d2song song hoặc trùng nhau.
Lấy điểm M(1; 3) ∈ d1, thay tọa độ của M vào phương trình d2, ta được: 5. 1 − 2. 3 + 9 = 0
⇒ M ∉ d2.
⇒ d1 // d2.
Vậy đường thẳng d1 song song với đường thẳng d2.
c) Đường thẳng d1 có VTPT là = (−1; 3) ⇒ = (3; 1) là vectơ pháp tuyến của d1.
Đường thẳng d2 có VTPT là = (3; 1)
⇒ = .
Do đó, d1 và d2 song song hoặc trùng nhau.
Lấy điểm N(2; 5) ∈ d1, thay tọa độ của điểm N vào phương trình d2, ta được: 3. 2 + 5 − 11 = 0
⇒ N ∈ d2.
Suy ra d1 trùng d2.
Vậy hai đường thẳng d1 và d2 trùng nhau.
Lời giải bài tập Toán 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ hay, chi tiết khác: