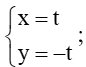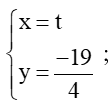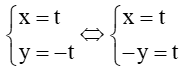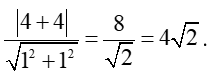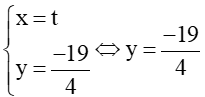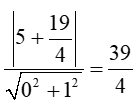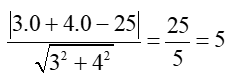Bài 7 trang 58 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10
Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau:
Giải Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 7 trang 58 Toán lớp 10 Tập 2: Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau:
a) M(1; 2) và ∆: 3x – 4y + 12 = 0;
b) M(4; 4) và ∆:
c) M(0; 5) và ∆:
d) M(0; 0) và ∆: 3x + 4y – 25 = 0.
Lời giải:
a) Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:
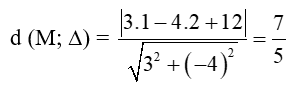
Vậy khoảng cách từ điểm M đến đường thẳng ∆ là .
b) Xét đường thẳng ∆:
⇒ x = - y
⇔ x + y = 0
Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:
d(M; ∆) =
Vậy khoảng cách từ điểm M đến đường thẳng ∆ là .
c) Xét đường thẳng ∆:
⇔ y + = 0
Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:
d(M; ∆) =
Vậy khoảng cách từ điểm M đến đường thẳng ∆ là .
d) Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:
d(M; ∆) =
Vậy khoảng cách từ điểm M đến đường thẳng ∆ là 5.
Lời giải bài tập Toán 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ hay, chi tiết khác: