Thực hành 6 trang 57 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh A(1; 1), B(5; 2), C(4; 4). Tính độ dài các đường cao của tam giác ABC.
Giải Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ
Thực hành 6 trang 57 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh A(1; 1), B(5; 2), C(4; 4). Tính độ dài các đường cao của tam giác ABC.
Lời giải:
+) Ta có: (4; 1)
Đường thẳng AB nhận (4; 1) làm vectơ chỉ phương nên vectơ pháp tuyến của AB là (1; -4). Khi đó phương trình đường thẳng AB là:
1(x – 1) – 4(y – 1) = 0
⇔ x – 4y + 3 = 0.
Độ dài đường cao kẻ từ C là khoảng cách từ điểm C đến đường thẳng AB:
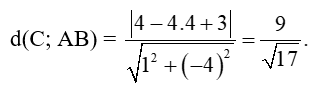
+) Ta có:(3; 3)
Đường thẳng AC nhận (3; 3) làm vectơ chỉ phương nên vectơ pháp tuyến của AC là (1; -1). Khi đó phương trình đường thẳng AC là:
1(x – 1) – 1(y – 1) = 0
⇔ x – y = 0.
Độ dài đường cao kẻ từ B là khoảng cách từ điểm B đến đường thẳng AC:
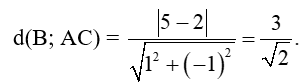
+) Ta có: (-1; 2)
Đường thẳng BC nhận (-1; 2) làm vectơ chỉ phương nên vectơ pháp tuyến của BC là (2; 1). Khi đó phương trình đường thẳng BC là:
2(x – 4) + 1(y – 4) = 0
⇔ 2x + y – 12 = 0.
Độ dài đường cao kẻ từ A là khoảng cách từ điểm A đến đường thẳng BC:
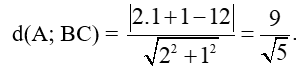
Vậy khoảng cách của các đường cao kẻ từ đỉnh A, B, C của tam giác lần lượt là: .
Lời giải bài tập Toán 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ hay, chi tiết khác:

