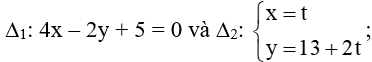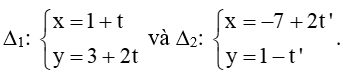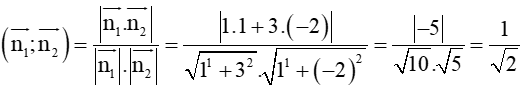Thực hành 5 trang 56 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10
Tìm số đo của góc giữa hai đường thẳng ∆ và ∆ trong các trường hợp sau:
Giải Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ
Thực hành 5 trang 56 Toán lớp 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng ∆1 và ∆2 trong các trường hợp sau:
a) ∆1: x + 3y – 7 = 0 và ∆2: x – 2y + 3 = 0;
b) 
c) 
Lời giải:
a) Đường thẳng ∆1: x + 3y – 7 = 0 có VTPT là = (1; 3).
Đường thẳng ∆2: x – 2y + 3 = 0 có VTPT là = (1; -2).
Ta có: cos(∆1; ∆2)
= cos
Suy ra (∆1; ∆2) = 45°.
Vậy góc giữa hai đường thẳng ∆1 và ∆2 là 45°.
b) Đường thẳng ∆1: 4x – 2y + 5 = 0 có vectơ pháp tuyến là (4; -2)
Đường thẳng ∆2: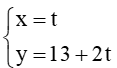
có vectơ chỉ phương (1; 2) hay vectơ pháp tuyến là (2; -1).
Ta có: a1.b2 – a2.b1 =4.(-1) – (-2).2 = 0. Do đó hai vectơ và cùng phương.
Suy ra (∆1; ∆2) = 0°.
Vậy góc giữa hai đường thẳng ∆1 và ∆2 là 0°.
c) Đường thẳng ∆1: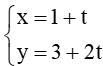 
có vectơ chỉ phương là (1; 2)
Đường thẳng ∆2: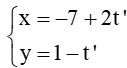 
có vectơ chỉ phương là (2; -1)
Ta có: . Do đó hai vectơ và vuông góc.
Suy ra (∆1; ∆2) = 90°.
Vậy góc giữa hai đường thẳng ∆1 và ∆2 là 90°.
Lời giải bài tập Toán 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ hay, chi tiết khác:
