Hoạt động khám phá 1 trang 46 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

❮ Bài trước Bài sau ❯

Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M(x; y) và cho hai vectơ = (a; b) và = (-b; a) khác vectơ – không. Cho biết có giá song song hoặc trùng với ∆.

Giải Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ

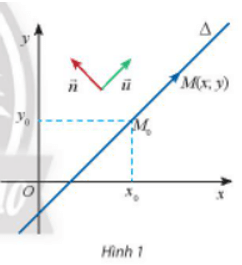
Hoạt động khám phá 1 trang 46 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và cho hai vectơ $\vec{n}$ = (a; b) và $\vec{u}$ = (-b; a) khác vectơ – không. Cho biết $\vec{u}$ có giá song song hoặc trùng với ∆.

a) Tính tích vô hướng $\vec{n}$ . $\vec{u}$ và nêu nhận xét về phương của hai vectơ $\vec{n}$ , $\vec{u}$ .

b) Gọi M(x; y) là điểm di động trên ∆. Chứng tỏ rằng vectơ $\vec{M_{0} M}$ luôn cùng phương với vectơ $\vec{u}$ và luôn vuông góc với vectơ $\vec{n}$ .

Hoạt động khám phá 1 trang 46 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

Lời giải:

a) Ta có: $\vec{n} . \vec{u}$ = a.(-b) + b.a = 0.

Do đó $\vec{n} ⊥ \vec{u}$ .

Vậy hai vectơ $\vec{n}$ , $\vec{u}$ có phương vuông góc với nhau.

b) Vì $\vec{u}$ có giá song song hoặc trùng với ∆ mà $\vec{M_{0} M}$ trùng với ∆ nên $\vec{u}$ có giá song song hoặc trùng với $\vec{M_{0} M}$ .

Do đó $\vec{u}$ cùng phương với $\vec{M_{0} M}$ .

c) Từ ý b) ta có $\vec{u}$ cùng phương với $\vec{M_{0} M}$

Mặt khác vectơ $\vec{u}$ vuông góc với vectơ $\vec{n}$ nên $\vec{u}$ vuông góc với $\vec{M_{0} M}$ .

Lời giải bài tập Toán 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯