15 Bài tập Tam giác cân. Đường trung trực của đoạn thẳng (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Tam giác cân. Đường trung trực của đoạn thẳng Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.
15 Bài tập Tam giác cân. Đường trung trực của đoạn thẳng (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7
Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa:
Câu 1. Cho tam giác ABC cân tại A. Khẳng định đúng là
A. AB = AC;
B. AB = BC;
C. A ^ = B ^
D. BC = AC.
Hiển thị đáp án
Đáp án đúng là: A
Tam giác ABC cân tại A thì AB = AC; B ^ C ^
Câu 2. Khẳng định nào sau đây sai ?
A. Tam giác cân là tam giác có hai cạnh bằng nhau ;
B. Tam giác đều là tam giác có 3 cạnh bằng nhau ;
C. Tam giác đều có 3 góc bằng nhau và bằng 60° ;
D. Tam giác cân có thể có hai góc tù.
Hiển thị đáp án
Đáp án đúng là: D
Tam giác cân có:
- Hai cạnh bằng nhau;
- Hai góc ở đáy bằng nhau.
Tam giác đều có:
- Ba cạnh bằng nhau.
- Ba góc bằng nhau và bằng 60°
Giải sử tam giác ABC cân tại A⇒B ^ C ^
Mà tổng 3 góc trong tam giác là 180°
⇒ B ^ = C ^ 180 ° − A ^ 2 90 ° − A ^ 2
Vậy trong tam giác cân có hai góc ở đáy luôn là góc nhọn, do đó không thể có hai góc tù.
Câu 3. Đường trung trực của một đoạn thẳng là
A. đường thẳng vuông góc với đoạn thẳng đó;
B. đường thẳng vuông góc với đoạn thẳng tại một điểm nằm giữa đoạn thẳng đó ;
C. đường thẳng vuông góc với đoạn thẳng đó tại trung điểm ;
D. đường thẳng đi qua trung điểm của đoạn thẳng đó .
Hiển thị đáp án
Đáp án đúng là: C
Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
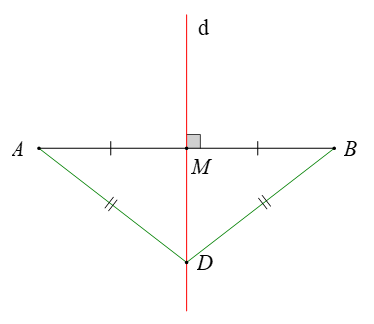
Ví dụ: Đường thẳng d vuông góc với đoạn AB tại M và M là trung điểm của AB. Khi đó d được gọi là đường trung trực của đoạn thẳng AB.
Câu 4. Cho điểm D nằm trên đường trung trực của đoạn thẳng AB. Khẳng định đúng là
A. DA > DB ;
B. DA = DB ;
C. DA < DB ;
D. DA ≥ DB .
Hiển thị đáp án
Đáp án đúng là: B
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Đường thẳng d là đường trung trực của đoạn thẳng AB và D ∈ d.
Khi đó DA = DB.
Câu 5. Cho tam giác ABC có A ^ = B ^
A. Tam giác ABC là tam giác đều ;
B. Tam giác ABC cân tại A ;
C. Tam giác ABC cân tại B ;
D. Tam giác ABC cân tại C .
Hiển thị đáp án
Đáp án đúng là: D
Tam giác ABC có A ^ = B ^
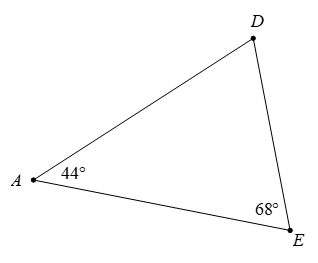
Câu 6. Cần thêm điều kiện gì để tam giác EAD trong hình vẽ dưới đây là tam giác cân:
A. Không cần thêm điều kiện gì;
B. AE = AD ;
C. AE = DE ;
D.AD = DE.
Hiển thị đáp án
Đáp án đúng là: A
Xét tam giác EDA có: E ^ + A ^ + D ^ = 180 °
⇒ 68 ° + 44 ° + D ^ = 180 °
⇒ D ^ = 68 °
⇒ D ^ = E ^ = 68 °
⇒ Tam giác EDA cân tại A.
Vậy không cần thêm điều kiện gì.
Câu 7. Cho tam giác MNP cân tại M có MN = 6 cm; NP = 7 cm. Chu vi tam giác MNP là
A. 20 cm ;
B. 19 cm ;
C. 18 cm ;
D. 17 cm .
Hiển thị đáp án
Đáp án đúng là: B
Tam giác MNP cân tại M nên MN = MP ⇒ MP = MN = 6 cm
Chu vi tam giác MNP là: MN + NP + MP = 6 + 7 + 6 = 19 (cm)
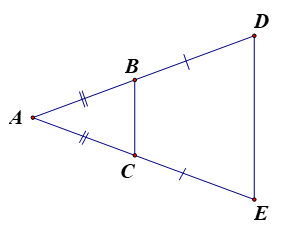
Câu 8. Hình dưới đây có các tam giác cân là
A. tam giác ABE ;
B. tam giác CAB ;
C. tam giác CAB và tam giác EAD ;
D. tam giác ABC .
Hiển thị đáp án
Đáp án đúng là: C
Xét tam giác CAB có: AB = AC
⇒ tam giác CAB cân tại A.
Có: AB = AC và BD = CE
Mà: AD = AB + BD; AE = AC + CE
Nên AD = AE
⇒ tam giác EAD cân tại A.
Câu 9. Cho tam giác MNP cân tại M có P ^ = 50 °
A. 50° ;
B. 80° ;
C. 90° ;
D. 130° .
Hiển thị đáp án
Đáp án đúng là: B
Tam giác MNP cân tại M nên N ^ = P ^ N ^ = P ^ = 50 °
Có N ^ + P ^ + M ^ = 180 °
⇒ 50 ° + 50 ° + M ^ = 180 °
⇒ M ^ = 80 °
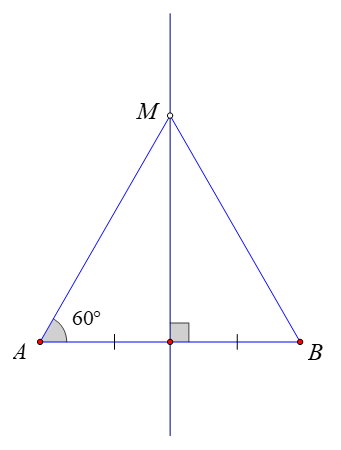
Câu 10. Cho điểm M thuộc đường trung trực của đoạn thẳng AB sao cho góc MAB bằng 60°. Khẳng định đúng nhất là
A. Tam giác MAB là tam giác cân tại M ;
B. Tam giác MAB đều;
C. Tam giác MAB là tam giác vuông cân ;
D. Tam giác MAB là tam giác tù .
Hiển thị đáp án
Đáp án đúng là: B
M thuộc đường trung trực của đoạn thẳng AB nên MA = MB (tính chất đường trung trực)
Do đó tam giác MAB cân tại M
Mà M A B ^ = 60 °
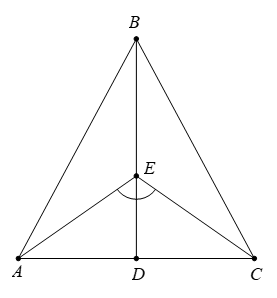
Câu 11. Cho hình vẽ dưới đây. Tam giác ABC cân tại B, D là trung điểm của AC. Biết A E C ^ = 110 ° A B E ^ + B A E ^
A. 20° ;
B. 110° ;
C. 55° ;
D. 70° .
Hiển thị đáp án
Đáp án đúng là: C
Xét tam giác BAD và tam giác BCD có:
BA = BC ( Δ A B C
AD là cạnh chung
AD = CD (D là trung điểm của AC)
⇒ Δ B A D = Δ B C D
⇒ B D A ^ = B D C ^
Mà B D A ^ + B D C ^ = 180 °
Nên B D A ^ = B D C ^ = 90 °
Xét tam giác ADE vuông tại D và tam giác CDE vuông tại D có:
AD = CD
DE là cạnh chung
⇒ Δ A D E = Δ C D E
⇒ A E D ^ = C E D ^
Mà A E C ^ = 110 °
⇒ A E D ^ = C E D ^ = A E C ^ 2 = 55 °
Ta có góc AED là góc ngoài tại đỉnh E của tam giác ABE nên
A B E ^ + B A E ^ = A E D ^ = 55 °
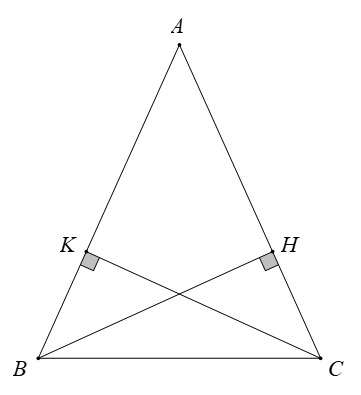
Câu 12. Cho hình vẽ dưới đây, biết tam giác ABC cân tại A. Khẳng định sai là
A. BH = BC ;
B. AB = AC ;
C. Δ B H A = Δ C K A
D. A B C ^ = A C B ^
Hiển thị đáp án
Đáp án đúng là: A
Tam giác ABC cân tại A ⇒ AB = AC và A B C ^ = A C B ^
Xét tam giác BHA (vuông tại H) và tam giác CKA (vuông tại K) có:
AB = AC ( Δ A B C
A ^
⇒ Δ B H A = Δ C K A
⇒ BH = CK (hai cạnh tương ứng)
Vậy khẳng định A sai.
Câu 13. Cho tam giác ABC cân tại A. I là trung điểm của đoạn thẳng BC.
Khẳng định đúng nhất là
A. Δ A I B = Δ A I C
B. AI ⊥ BC;
C. AI là tia phân giác của góc BAC;
D. Cả A, B và C đều đúng .
Hiển thị đáp án
Đáp án đúng là: D
Xét tam giác AIB và tam giác AIC có:
AB = AC (Δ A B C
BI = CI (theo giả thiết)
AI là cạnh chung
⇒ Δ A I B = Δ A I C
⇒ A I B ^ = A I C ^
Mà A I B ^ + A I C ^ = 180 °
⇒ A I B ^ = A I C ^ = 90 °
⇒ AI ⊥ BC
Vì Δ A I B = Δ A I C
⇒ I A B ^ = I A C ^
⇒ AI là tia phân giác của góc BAC
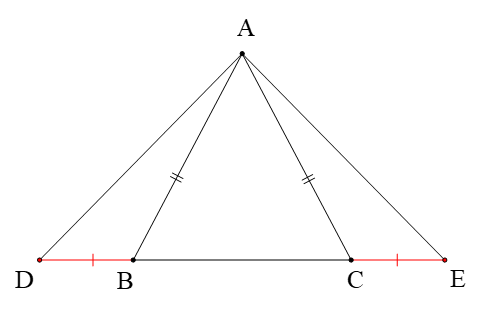
Câu 14. Cho hình vẽ dưới đây, biết tam giác ABC cân tại A và BD = CE. Khẳng định đúnglà
A. Tam giác ADC cân tại A ;
B. Tam giác ABE cân tại A ;
C. Tam giác ADE cân tại A ;
D. Cả A, B và D đều sai .
Hiển thị đáp án
Đáp án đúng là: C
Δ A B C A B C ^ = A C B ^
Mà: A B C ^ + A B D ^ = 180 °
A C B ^ + A C E ^ = 180 °
⇒ A B D ^ = A C E ^
Xét tam giác ADB và tam giác AEC có:
AB = AC (Δ A B C
A B D ^ = A C E ^
BD = CE (theo giả thiết)
⇒ Δ A D B = Δ A E C
⇒ AD = AE (hai cạnh tương ứng)
⇒ Δ A D E
Câu 15. Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Khẳng định sai là
A. AH ⊥ BC;
B. AH là đường trung trực của đoạn thẳng BC;
C. HB = HC ;
D. HA = HB .
Hiển thị đáp án
Đáp án đúng là: D
Xét tam giác ABH và tam giác ACH có:
AB = AC (Δ A B C
B A H ^ = C A H ^
AH là cạnh chung
⇒ Δ A B H = Δ A C H
⇒ HB = HC (hai cạnh tương ứng) (1)
Và A H B ^ = A H C ^
Mà A H B ^ + A H C ^ = 180 °
⇒ A H B ^ = A H C ^ = 90 °
Từ (1) và (2) ⇒ AH là đường trung trực của đoạn thẳng BC