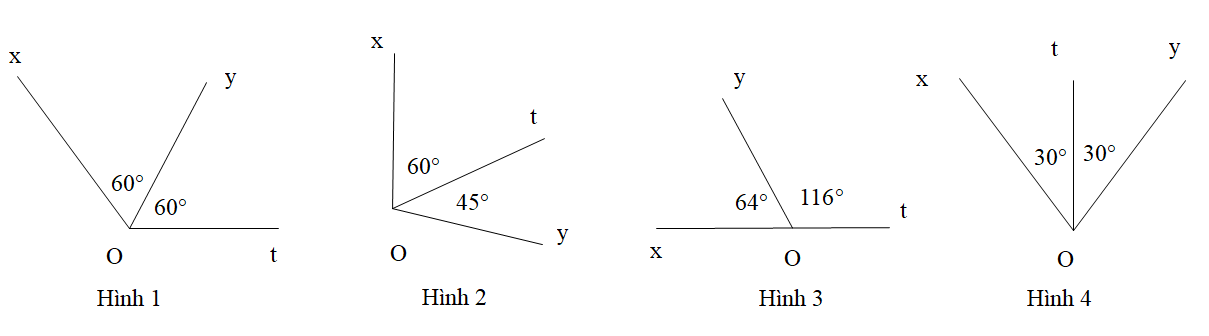15 Bài tập Góc ở vị trí đặc biệt. Tia phân giác của một góc (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

---

Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Góc ở vị trí đặc biệt. Tia phân giác của một góc Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Góc ở vị trí đặc biệt. Tia phân giác của một góc (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Xem thử

Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Câu 1. Chọn đáp án đúng. Tính chất của hai góc kề bù là:

A. Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau;

B. Hai góc kề bù có tổng số đo bằng 180^o;                        

C. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia;                                                                        

D. Hai góc bằng nhau.

Hiển thị đáp án

Đáp án đúng là: B

Đáp án A là định nghĩa về hai góc kề bù.

Tính chất của hai góc kề bù: hai góc kề bù có tổng số đo bằng 180^o.

Câu 2. Chọn đáp án sai. Hai góc đối đỉnh là:

A. Hai góc bằng nhau;

B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia;

C. Hai góc có tổng số đo bằng 180^o;

D. Hai góc được tạo bởi hai đường thẳng cắt nhau.

Hiển thị đáp án

Đáp án đúng là: C

Hai góc có tổng số đo bằng 180^o là hai góc bù nhau.

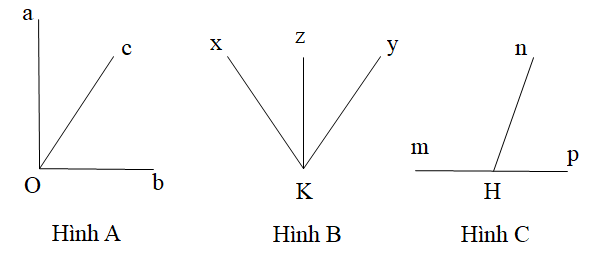
Câu 3. Trong các hình dưới đây hình nào chứa 2 góc kề bù.

A. Hình A;

B. Hình B;

C. Hình C;

D. Không có hình nào.

Hiển thị đáp án

Đáp án đúng là: C

Hình C chứa hai góc kề bù do hai góc đó kề nhau và tổng số đo 2 góc đó bằng 180^o.

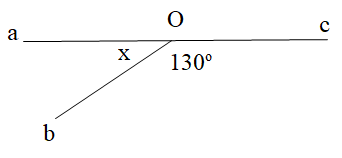
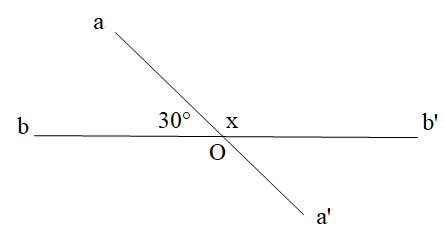
Câu 4. Tìm số đo x:

A.65°;

B.120°;

C.95°;

D. 50°.

Hiển thị đáp án

Đáp án đúng là: D

Ta có góc aOb và góc bOc là hai góc kề bù nên $\widehat{aOb}+\widehat{bOc}=180°$.

Suy ra $x=\widehat{aOb}=180°-\widehat{bOc}=180°-130°=50°$.

Vậy x = 50^o.

Câu 5. Hai góc đối đỉnh thì:

A. Có hiệu bằng 180°;

B.Có tổng bằng 180°;

C.Kề nhau;

D.Bằng nhau.

Hiển thị đáp án

Đáp án đúng là: D

Hai góc đối đỉnh thì bằng nhau.

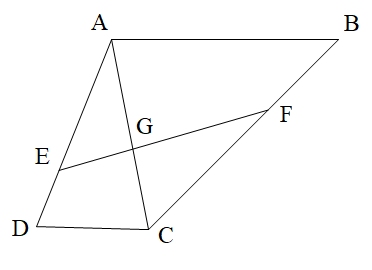
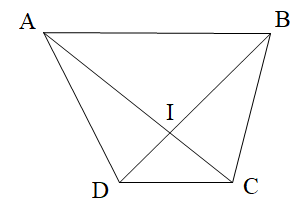
Câu 6. Quan sát hình bên và chỉ ra hai góc đối đỉnh.

A. Góc AGE và góc FGC;

B. Góc FGA và góc FGC;

C. Góc FBA và góc GFC;

D. Góc BCG và góc CAD.

Hiển thị đáp án

Đáp án đúng là: A

Các cặp góc đối đỉnh trong hình trên là góc AGE và góc FGC; góc AGF và góc EGC.

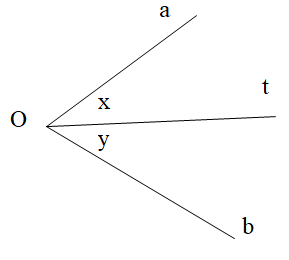
Câu 7. Cho hình vẽ,

Biết $\widehat{aOb}=70°$ và tia Ot là tia phân giác góc xOy. Tính x, y.

A. $x=y=35°$;

B. $x=35°;y=45°$;

C. $x=45°;y=35°$ ;

D. $x=y=70°$.

Hiển thị đáp án

Đáp án đúng là: A

Ta có tia Ot là tia phân giác góc xOy nên suy ra $\widehat{aOt}=\widehat{tOb}=\frac{\widehat{aOb}}{2}=\frac{70°}{2}=35°$

Suy ra $x=\widehat{aOt}=35°;y=\widehat{tOb}=35°$

Vậy x = y = 35^o.

Câu 8. Chọn đáp án đúng.

A.$\widehat{AID}$ và $\widehat{CIB}$ là hai góc kề bù;

B. $\widehat{ABC}$ và $\widehat{ADC}$ là hai góc kề bù;

C. $\widehat{AIB}$ và $\widehat{BIC}$ là hai góc kề bù;

D. $\widehat{AIB}$ và $\widehat{DIC}$ là hai góc kề bù.

Hiển thị đáp án

Đáp án đúng là: C

$\widehat{AID}$ và $\widehat{CIB}$ là hai góc hai góc kề bù (sai, vì $\widehat{AID}$ và $\widehat{CIB}$ là hai góc hai góc đối đỉnh loại phương án A);

$\widehat{ABC}$ và $\widehat{ADC}$ là hai góc kề bù (sai, vì $\widehat{ABC}$ và $\widehat{ADC}$ là hai góc của tứ giác ABCD, loại phương án B);

$\widehat{AIB}$ và $\widehat{BIC}$ là hai góc kề bù (đúng, chọn phương án C);

$\widehat{AIB}$ và $\widehat{DIC}$ là hai góc kề bù (sai, vì $\widehat{AIB}$ và $\widehat{DIC}$ là hai góc đối đỉnh, loại phương án D).

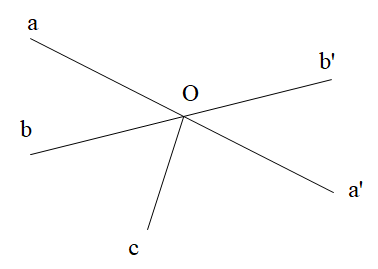
Câu 9.Góc aOb và góc b’Oa’ là:

A. Hai góc bù nhau;

B. Hai góc kề bù;

C. Hai góc đối đỉnh;

D. Hai góc kề nhau.

Hiển thị đáp án

Đáp án đúng là: C

Góc aOb và góc b’Oa’ là hai góc đối đỉnh.

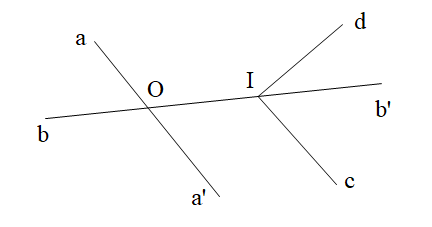
Câu 10.Cho hình vẽ. Em hãy chỉ ra cặp góc đối đỉnh (khác góc bẹt).

A. $\widehat{aOb}$ và $\widehat{aO{b}^{\text{'}}}$ ;

B. $\widehat{cI{b}^{\text{'}}}$ và $\widehat{bId}$ ;

C. $\widehat{aO{b}^{\text{'}}}$ và $\widehat{aOd}$ ;

D. $\widehat{aOb}$ và $\widehat{a^{\text{'}}O{b}^{\text{'}}}$ .

Hiển thị đáp án

Đáp án đúng là: D

Hai góc đối đỉnh (khác góc bẹt) là $\widehat{aOb}$ và $\widehat{a^{\text{'}}O{b}^{\text{'}}}$ .

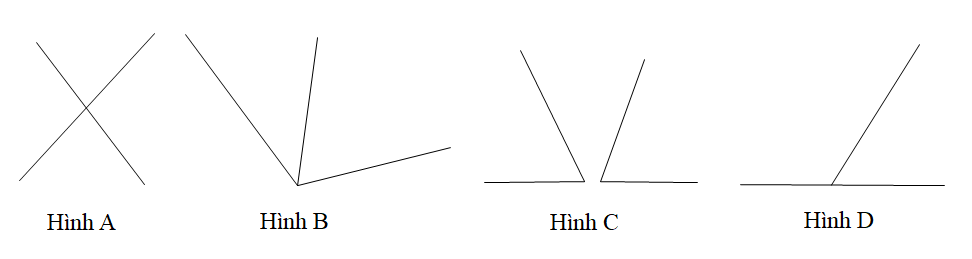
Câu 11. Trong các hình dưới đây hình nào không chứa hai góc kề nhau.

A. Hình A;

B. Hình B;

C. Hình C;

D. Hình D.

Hiển thị đáp án

Đáp án đúng là: C.

Hai góc kề nhau là có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.

Hình C không chứa hai góc kề nhau vì hai góc này không có đỉnh chung và cạnh chung.

Suy ra chọn đáp án C.

Câu 12. Khi Ot là tia phân giác của góc xOy thì

A. $\widehat{xOt}=\widehat{yOt}=\frac{1}{3}\widehat{xOy}$ ;

B. $\widehat{xOt}=\widehat{yOt}=\frac{1}{2}\widehat{xOy}$ ;

C. $\widehat{xOt}+\widehat{yOt}=\frac{1}{2}\widehat{xOy}$ ;

D. $\widehat{xOt}+\widehat{yOt}=\frac{1}{3}\widehat{xOy}$ .

Hiển thị đáp án

Đáp án đúng là: B

Tính chất của tia phân giác:

Khi Ot là tia phân giác của góc xOy thì $\widehat{xOt}=\widehat{yOt}=\frac{1}{2}\widehat{xOy}$.

Câu 13. Hai đường thẳng xx’, yy’ cắt nhau và trong các góc tạo thành có một góc vuông được gọi là

A. Hai đường thẳng song song;

B. Hai đường thẳng trùng nhau;

C. Hai đường thẳng cắt nhau;

D. Hai đường thẳng vuông góc.

Hiển thị đáp án

Đáp án đúng là: D

Hai đường thẳng xx’, yy’ cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc.

Câu 14. Tìm số đo x:

A. 120^o;

B. 60^o;

C. 30^o;

D. 150^o.

Hiển thị đáp án

Đáp án đúng là: D

Ta có góc aOb và góc aOb’ là hai góc kề bù nên $\widehat{aOb}+\widehat{aOb\text{'}}=180°$

Suy ra $x=\widehat{aOb\text{'}}=180°-\widehat{aOb}=180°-30°=150°$ .

Câu 15. Tia Ot nào trong các hình dưới đây là tia phân giác của góc xOy.

A. Hình 1;

B. Hình 2;

C. Hình 3;

D. Hình 4.

Hiển thị đáp án

Đáp án đúng là: D

Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Hình 1 và hình 3 tia Ot không nằm trong góc nên tia Ot không phải tia phân giác của góc xOy.

Hình 2 có tia Ot nằm trong góc nhưng không tạo với hai cạnh của góc đó hai góc bằng nhau nên tia Ot trong hình 2 không phải tia phân giác của góc xOy.

Chỉ có hình 4 là tia Ot nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau nên Ot là tia phân giác của góc xOy.

Do đó chọn phương án D.

Xem thử