Tính chất ba đường trung trực của tam giác (Lý thuyết Toán lớp 7) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tính chất ba đường trung trực của tam giác (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Tính chất ba đường trung trực của tam giác

1. Đường trung trực của tam giác

– Trong một tam giác, đường trung trực của mỗi cạnh được gọi là đường trung trực của tam giác đó.

Chú ý: Đường trung trực của một tam giác có thể không đi qua đỉnh nào của tam giác.

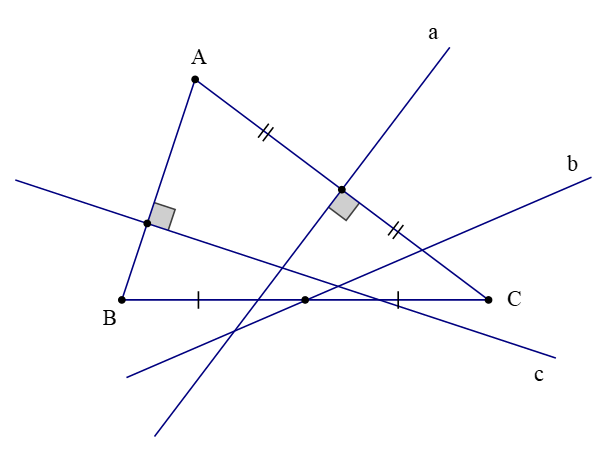
Ví dụ: Quan sát hình vẽ và chỉ ra các đường trung trực của tam giác (nếu có):

Hướng dẫn giải

Đường thẳng a vuông góc với AC tại trung điểm của cạnh đó nên đường thẳng a là trung trực của ∆ABC.

Đường thẳng b đi trung điểm của BC nhưng không vuông góc với BC tại trung điểm của cạnh đó nên đường thẳng b không là đường trung trực của ∆ABC.

Đường thẳng c ⊥ AB nhưng không vuông góc tại trung điểm của cạnh đó nên đường thẳng c không là đường trung trực của ∆ABC.

– Nhận xét: Mỗi tam giác có 3 đường trung trực.

2. Tính chất ba đường trung trực của tam giác

– Ba đường trung trực của một tam giác cùng đi qua một điểm.

Nhận xét:

+ Để xác định giao điểm ba đường trung trực của một tam giác, ta chỉ cần vẽ hai đường trung trực bất kì và xác định giao điểm của hai đường đó.

+ Giao điểm ba đường trung trực của một tam giác cách đều ba đỉnh của tam giác đó.

Do đó, trong một tam giác ba đường trung trực cùng đi qua một điểm và điểm đó cách đều ba đỉnh của tam giác.

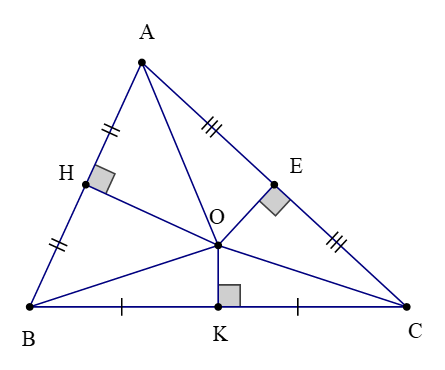
Ví dụ: Cho ∆ABC có ba đường trung trực của AB, BC, AC cắt nhau tại O, tương ứng cắt AB, BC, CA lần lượt tại H, K, E. Chứng minh rằng: BK < OA < OC + BC.

Hướng dẫn giải

Vì O là giao điểm của ba đường trung trực trong ∆ABC nên OA = OB = OC.

Xét ∆OBK vuông tại K nên OB > BK (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất).(1)

∆OBC có OB < OC + BC (bất đẳng thức trong tam giác)

Mà OA = OB

Do đó OA < OC + BC(2)

Từ (1) và (2) suy ra BK < OA < OC + BC

Vậy BK < OA < OC + BC.

Bài tập Tính chất ba đường trung trực của tam giác

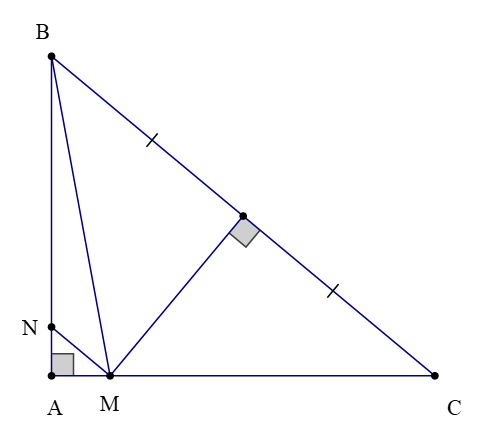
Bài 1. Cho ∆ABC vuông tại A, có $\hat{\text{C}}=40°$ và đường trung trực của BC cắt AC tại M. Qua M kẻ đường thẳng song song với BC cắt AB tại N. Tính số đo các góc của ∆BMN.

Hướng dẫn giải

Theo bài ta có: M nằm trên đường trung trực của BC nên BM = CM.

Suy ra ∆BMC cân tại M nên $\hat{\text{C}}=\widehat{\text{CBM}}=40°$

Vì MN // BC nên $\widehat{\text{NMB}}=\widehat{\text{CBM}}=40°$ (hai góc so le trong)

Xét ∆ABC vuông tại A có:

$\widehat{\text{ABC}}+\hat{\text{C}}=90°$(tổng của hai góc nhọn trong tam giác vuông bằng 90°)

Suy ra $\widehat{\text{ABC}}=90°-\hat{\text{C}}=90°-40°=50°$

Ta lại có $\widehat{NBM}+\widehat{\text{MBC}}=\widehat{\text{NBC}}=\widehat{\text{ABC}}$

Suy ra $\widehat{\text{NBM}}=\widehat{\text{ABC}}-\widehat{\text{MBC}}=50°-40°=10°.$

Do MN // BC nên $\widehat{\text{MNB}}+\widehat{\text{NBC}}=180°$ (hai góc trong cùng phía)

Suy ra $\widehat{\text{MNB}}=180°-\widehat{\text{NBC}}=180°-50°=130°.$

Vậy ∆BMN có $\widehat{\text{MNB}}=130°$ ;$\widehat{\text{NBM}}=10°$ ; $\widehat{\text{NMB}}=40°$ .

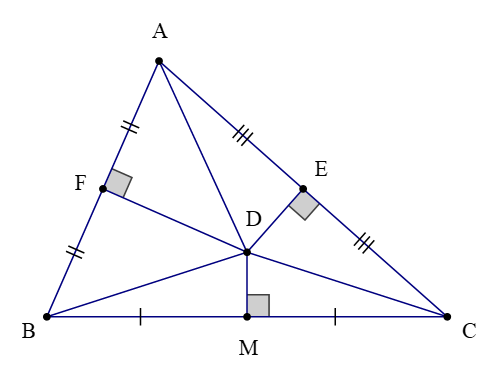
Bài 2. Cho ∆ABC có D là giao điểm các đường trung trực của tam giác. Kẻ DE ⊥ AC tại E; DF ⊥ AB tại F và DM ⊥ BC tại M. Chứng minh rằng $\text{DA >}\frac{\text{AB + AC +BC}}{6}$ .

Hướng dẫn giải

Ta có D là giao điểm các đường trung trực của ∆ABC và DE ⊥ AC tại E; DF ⊥ AB tại F và DM ⊥ BC tại M.

Suy ra DF, DM, DE lần lượt là đường trung trực của AB, BC, AC.

Do đó F, M, E lần lượt là trung điểm của AB, BC, AC

Suy ra $AF=\frac{1}{2}\text{AB, BM =}\frac{1}{2}\text{BC, CE =}\frac{1}{2}\text{AC}$

∆ADF vuông tại F nên DA > AF (vì cạnh huyền lớn nhất)

Suy ra $\text{DA >}\frac{1}{2}\text{AB}$ (1)

∆DBM vuông tại M nên DB > BM (vì cạnh huyền lớn nhất)

Suy ra $\text{DB >}\frac{1}{2}\text{BC}$ (2)

∆CDE vuông tại E nên DC > EC (vì cạnh huyền lớn nhất)

Suy ra $\text{DC >}\frac{1}{2}\text{AC}$ (3)

Từ (1), (2) và (3) suy ra $\text{DA + DB + DC >}\frac{1}{2}AB+\frac{1}{2}BC+\frac{1}{2}AC$

Hay $\text{DA + DB + DC >}\frac{1}{2}\text{(AB +}BC+AC\text{)}$

Vì D là giao điểm của các đường trung trực trong ∆ABC nên DA = DB = DC.

Do đó $\text{DA + DB + DC >}\frac{1}{2}\text{(AB +}BC+AC\text{)}$

Hay $\text{DA + DA + DA >}\frac{1}{2}\text{(AB +}BC+AC\text{)}$

Suy ra $\text{3DA >}\frac{1}{2}\text{(AB +}BC+AC\text{).}$

Suy ra $\text{DA >}\frac{\text{AB + BC +AC}}{6}.$

Vậy $\text{DA >}\frac{\text{AB + AC +BC}}{6}$ .

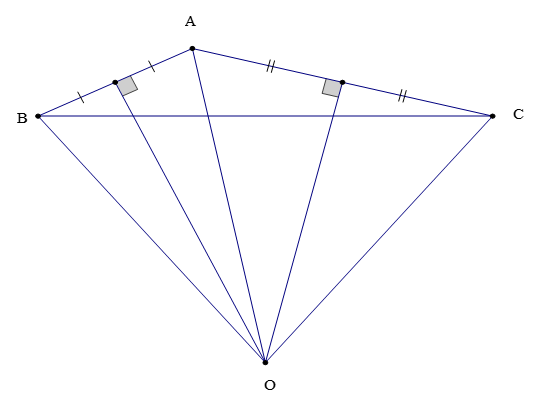
Bài 3. Cho ∆ABC có góc A là góc tù, gọi O là giao điểm các đường trung trực của tam giác sao cho $\widehat{\text{BOC}}=84°$ . Tính $\widehat{\text{BAC}}$ .

Hướng dẫn giải

Theo bài ta có: O là giao điểm các đường trung trực của ∆ABC.

Do đó OA = OB = OC (tính chất đường trung trực trong tam giác).

• Xét ∆OAB có OA = OB nên ∆OAB cân tại O.

Suy ra $\widehat{\text{OBA}}=\widehat{\text{OAB}}$ (tính chất tam giác cân)

∆OAB có $\widehat{\text{BOA}}+\widehat{\text{OBA}}+\widehat{\text{OAB}}=180°$ (tổng ba góc trong tam giác)

Suy ra $\widehat{\text{BOA}}=180°-\widehat{\text{ABO}}-\widehat{\text{BAO}}$

Mà $\widehat{\text{OBA}}=\widehat{\text{OAB}}$ (chứng minh trên)

Nên $\widehat{\text{BOA}}=180°-2\widehat{\text{BAO}}$ (1)

• Xét ∆OAC có OA = OC nên ∆OAC cân tại O.

Suy ra $\widehat{\text{OCA}}=\widehat{\text{OAC}}$ (tính chất tam giác cân).

∆OAC có $\widehat{\text{COA}}+\widehat{\text{OCA}}+\widehat{\text{OAC}}=180°$ (tổng ba góc trong tam giác)

Suy ra $\widehat{\text{COA}}=180°-\widehat{\text{ACO}}-\widehat{\text{CAO}}$

Mà $\widehat{\text{OCA}}=\widehat{\text{OAC}}$ (chứng minh trên)

Suy ra $\widehat{\text{COA}}=180°-2\widehat{\text{CAO}}$ (2)

Từ (1) và (2) suy ra:

$\widehat{\text{BOA}}+\widehat{\text{COA}}=180°-2\widehat{\text{BAO}}+180°-2\widehat{\text{CAO}}$

Hay $\widehat{\text{BOC}}=360°-2(\widehat{\text{BAO}}+\widehat{\text{CAO}})$

Suy ra $84°=360°-2\widehat{\text{BAC}}$

Suy ra $2\widehat{\text{BAC}}=360°-84°=276°$

Suy ra $\widehat{\text{BAC}}=276°:2=138°$

Vậy $\widehat{\text{BAC}}=138°$ .

Học tốt Tính chất ba đường trung trực của tam giác

Các bài học để học tốt Tính chất ba đường trung trực của tam giác Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác

• Giải sbt Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác