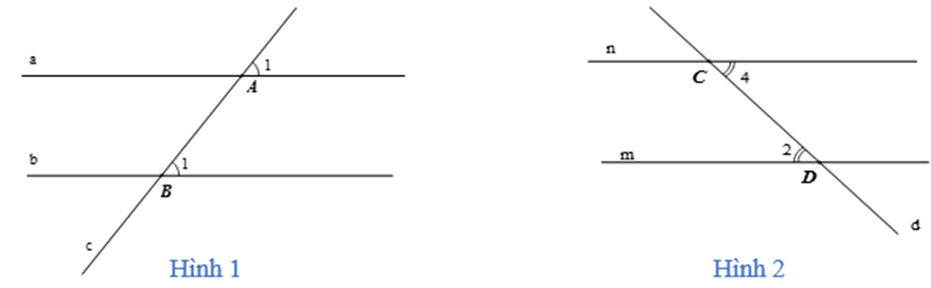Hai đường thẳng song song (Lý thuyết Toán lớp 7) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 3: Hai đường thẳng song song hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Hai đường thẳng song song (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Hai đường thẳng song song

1. Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.

Khi đó, ta thấy:

+ Góc A₁ và góc B₁ ở “cùng một phía” của đường thẳng c.

+ Góc A₁ ở “phía trên” đường thẳng a. Góc B₁ cũng ở “phía trên” đường thẳng b.

Hai góc A₁ và B₁ ở vị trí như thế được gọi là hai góc đồng vị.

+ Góc A₃ và góc B₁ ở “hai phía” của đường thẳng c.

+ Góc A₃ ở “phía dưới” của đường thẳng a. Góc B₁ lại ở “phía trên” của đường thẳng b.

Hai góc A₃ và B₁ ở vị trí như thế gọi là hai góc so le trong.

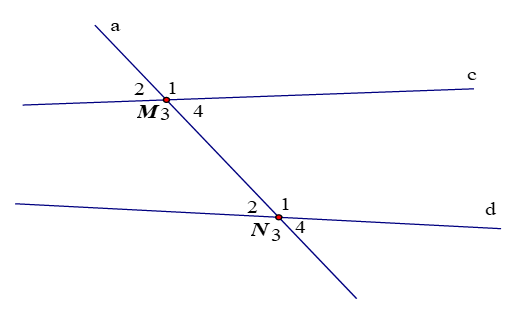
Ví dụ: Kể tên các cặp góc so le trong và đồng vị trong hình sau:

Hướng dẫn giải

Các cặp góc so le trong là: M₃ và N₁; M₄ và N₂.

Các cặp góc đồng vị là: M₁ và N₁; M₂ và N₂; M₃ và N₃; M₄ và N₄.

2. Dấu hiệu nhận biết hai đường thẳng song song

- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.

- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.

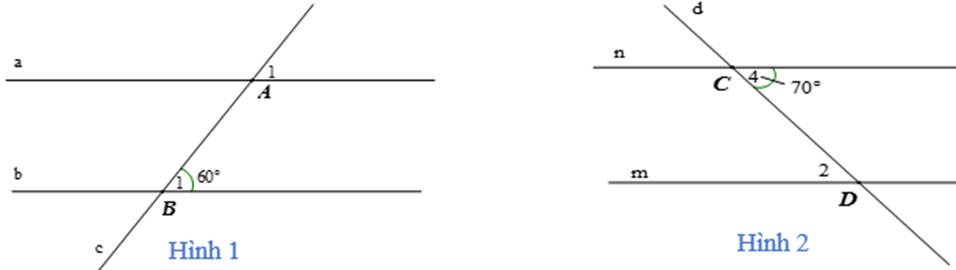
Ví dụ:

- Ở hình 1: Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau $\left(\widehat{A_1}=\widehat{B_1}\right)$ nên a // b.

- Ở hình 2: Đường thẳng d cắt hai đường thẳng m, n và trong các góc tạo thành có một cặp góc so le trong bằng nhau $\left(\widehat{C_4}=\widehat{D2}\right)$ nên m // n.

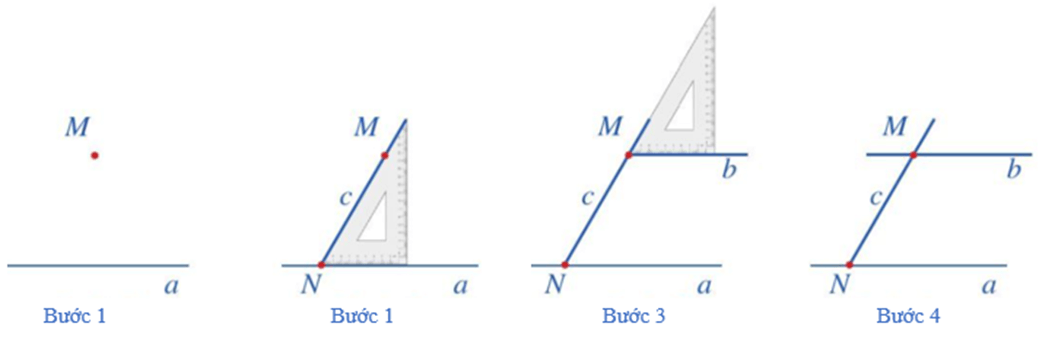
Ví dụ: Vẽ một đường thẳng b đi qua điểm M và song song với đường thẳng a (M ∉ a) bằng ê ke.

Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.

Bước 2: Đặt ê ke sao cho cạnh ngắn của góc vuông nằm trên đường thẳng a và cạnh huyền đi qua điểm M, vẽ theo cạnh huyền một phần đường thẳng c đi qua M (đường thẳng c cắt đường thẳng a tại điểm N).

Bước 3: Dịch chuyển ê ke sao cho cạnh huyền của ê ke vẫn nằm trên đường thẳng c còn cạnh ngắn của góc vuông đi qua điểm M, vẽ theo cạnh ngắn của góc vuông một phần đường thẳng b đi qua điểm M.

Bước 4: Vẽ hoàn thiện đường thẳng b.

Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.

3. Tiên đề Euclid về đường thẳng song song

Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.

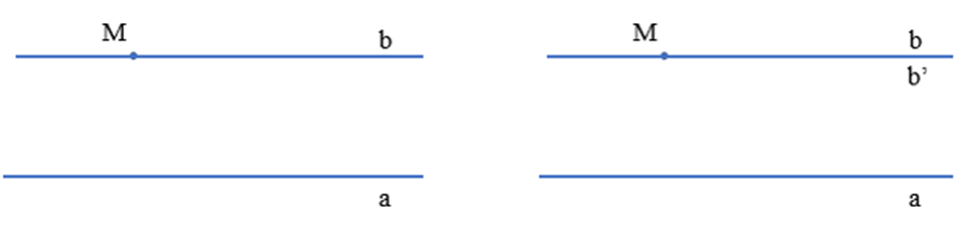
Ví dụ:

Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.

Và vẽ được đường thẳng b’ cũng đi qua M và b’ song song với a.

Khi đó theo Tiên đề Euclid thì b và b’ trùng nhau.

4. Tính chất của hai đường thẳng song song

Nếu một đường thẳng cắt hai đường thẳng song song thì:

- Hai góc đồng vị bằng nhau.

- Hai góc so le trong bằng nhau.

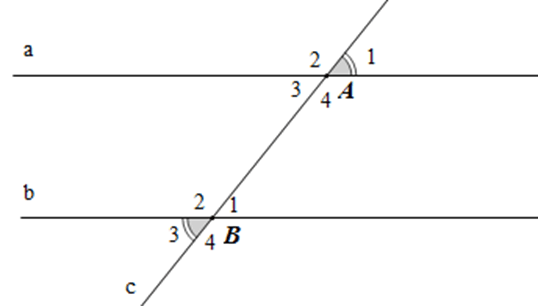
Ví dụ: Tính số đo các góc A₁ và góc D₂ ­ trong hai hình vẽ sau, biết a // b và m // n.

Hướng dẫn giải

- Hình 1: Do a // b nên ta có: $\widehat{A_1}=\widehat{B_1}$ (hai góc đồng vị), mà $\widehat{B_1}={60}^0$ nên $\widehat{A_1}=\widehat{B_1}={60}^0$.

Vậy $\widehat{A_1}={60}^0$.

- Hình 2: Do m // n nên: $\widehat{C_4}=\widehat{D_2}$ (hai góc so le trong), mà $\widehat{C_4}={70}^0$ nên $\widehat{C_4}=\widehat{D_2}=70$.

Vậy $\widehat{D_2}={70}^0$.

Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:

+ Hai góc so le ngoài bằng nhau.

+ Hai góc trong cùng phía có tổng số đo bằng 180⁰.

Ví dụ:

- Các cặp góc so le ngoài A₁ và B₃; A₂ và B₄; Khi đó: $\widehat{A_1}=\widehat{B_3}$ và $\widehat{A_2}=\widehat{B_4}$.

- Hai góc trong cùng phía: góc A₃ và góc B₂; góc A₄ và góc B₁.

Khi đó: $\widehat{A_3}+\widehat{B_2}={180}^0$; $\widehat{A_4}+\widehat{B_1}={180}^0$.

Bài tập Hai đường thẳng song song

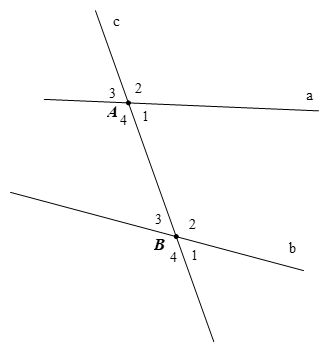
Bài 1: Hãy kể tên các cặp góc so le trong, đồng vị trong hình vẽ sau.

Hướng dẫn giải

- Các cặp góc so le trong là: A₁ và B₃; A₄ và B₂.

- Các cặp góc đồng vị là: A₁ và B₁; A₂ và B₂; A₃ và B₃; A₄ và B₄.

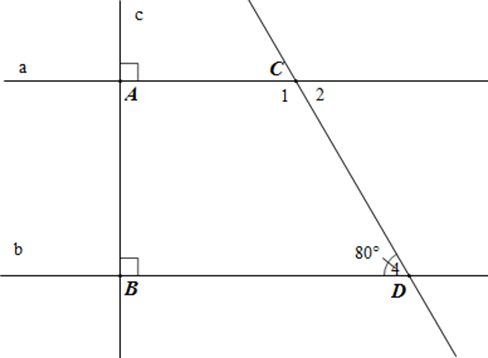
Bài 2: Cho hình vẽ sau:

a) Vì sao a // b?

b) Tính số đo các góc C₁, C₂ trong hình vẽ.

Hướng dẫn giải

a) Ta có góc A và góc B là hai góc đồng vị, mà $\hat{A}=\hat{B}={90}^0$.

Vậy nên a // b.

b) Ta có góc C₁ và D₄ là hai góc trong cùng phía.

Mà a // b nên $\widehat{C_1}+\widehat{D_4}={180}^0$

Suy ra $\widehat{C_1}={180}^0-\widehat{D_4}={180}^0-{80}^0={100}^0$.

Góc C₂ và góc D₄ ở vị trí so le trong nên $\widehat{C_2}=\widehat{D_4}={80}^0$.

Vậy $\widehat{C_1}={100}^0$; $\widehat{C_2}={80}^0$.

Học tốt Hai đường thẳng song song

Các bài học để học tốt Hai đường thẳng song song Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 3: Hai đường thẳng song song

• Giải sbt Toán 7 Bài 3: Hai đường thẳng song song