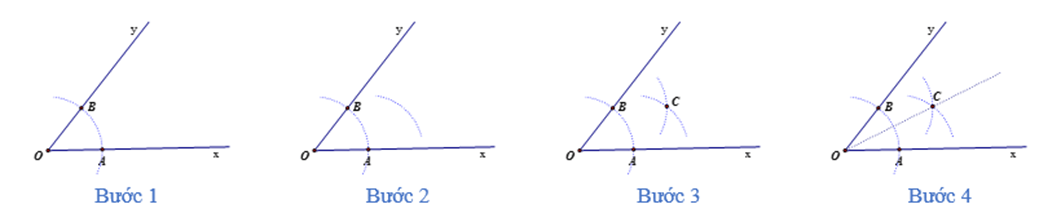Tổng hợp lý thuyết Toán 7 Chương 4 Cánh diều

---

Với Tổng hợp lý thuyết Toán 7 Chương 4: Góc. Đường thẳng song song sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tổng hợp lý thuyết Toán 7 Chương 4 Cánh diều

Lý thuyết tổng hợp Toán 7 Chương 4

1. Góc ở vị trí đặc biệt

a) Hai góc kề nhau

Hai góc kề nhau là hai góc có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.

Tính chất:

- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó. Khi đó hai góc xOy và yOz là hai góc kề nhau và $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox, Oz), ta cũng có: $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

b) Hai góc bù nhau. Hai góc kề bù

- Hai góc bù nhau là hai góc có tổng bằng 180⁰.

- Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.

Chú ý: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau là hai góc kề bù.

c) Hai góc đối đỉnh

- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Hai góc đối đỉnh thì bằng nhau.

2. Tia phân giác của một góc

a) Định nghĩa

Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

b) Vẽ tia phân giác của một góc

Cho góc xOy. Để vẽ tia phân giác của góc xOy ta có các cách sau:

Cách 1: Vẽ tia phân giác của một góc bằng thước thẳng và compa.

Bước 1: Trên tia Ox lấy điểm A bất kì (A khác O). Vẽ một phần đường tròn tâm O bán kính OA, cắt tia Oy tại điểm B.

Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.

Bước 3: Vẽ một phần đường tròn tâm B bán kính AO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.

Bước 4: Vẽ tia OC, ta được tia phân giác của góc xOy.

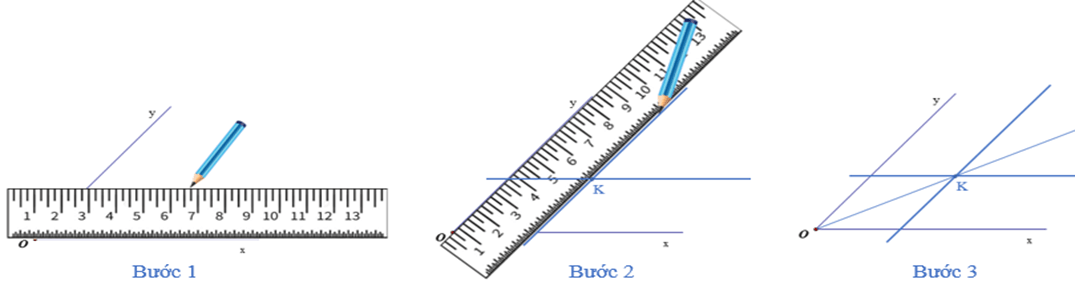
Cách 2: Dùng thước hai lề

Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với một trong hai cạnh của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh còn lại của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 3: Hai nét vạch ở bước 1 và bước 2 cắt nhau tại điểm K nằm trong góc xOy. Vẽ tia OK, ta được tia này là tia phân giác của góc xOy.

3.Hai đường thẳng song song

a) Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.

Khi đó, ta thấy:

+ Góc A₁ và góc B₁ ở “cùng một phía” của đường thẳng c.

+ Góc A₁ ở “phía trên” đường thẳng a. Góc B₁ cũng ở “phía trên” đường thẳng b.

Hai góc A₁ và B₁ ở vị trí như thế được gọi là hai góc đồng vị.

+ Góc A₃ và góc B₁ ở “hai phía” của đường thẳng c.

+ Góc A₃ ở “phía dưới” của đường thẳng a. Góc B₁ lại ở “phía trên” của đường thẳng b.

Hai góc A₃ và B₁ ở vị trí như thế gọi là hai góc so le trong.

b) Dấu hiệu nhận biết hai đường thẳng song song

- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.

- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.

Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.

c) Tiên đề Euclid về đường thẳng song song

Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.

d) Tính chất của hai đường thẳng song song

Nếu một đường thẳng cắt hai đường thẳng song song thì:

- Hai góc đồng vị bằng nhau.

- Hai góc so le trong bằng nhau.

Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:

+ Hai góc so le ngoài bằng nhau.

+ Hai góc trong cùng phía có tổng số đo bằng 180⁰.

4. Định lý

a) Định lí

Khẳng định có các tính chất sau thì được gọi là định lý:

- Là một phát biểu về một tính chất toán học;

- Tính chất toán học đó đã được chứng tỏ là đúng không dựa vào trực giác hay đo đạc,..

Nhận xét:

+ Định lý thường được phát biểu dưới dạng “Nếu … thì …”.

+ Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết, phần nằm sau từ “thì” là phần kết luận.

b) Chứng minh định lý

Chứng minh định lý là một tiến trình lập luận từ giả thiết suy ra kết luận là đúng.

Bài tập tổng hợp Toán 7 Chương 4

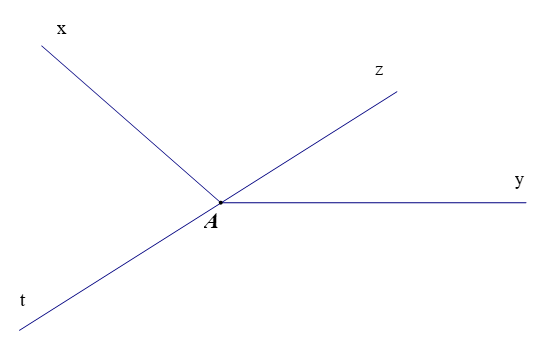
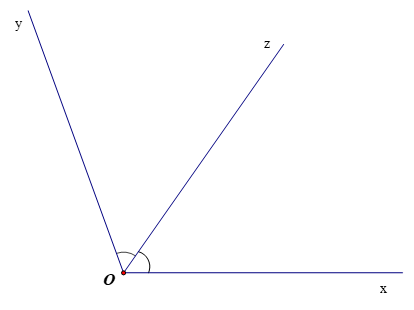
Bài 1: Kể tên các cặp góc kề nhau trong hình sau:

Hướng dẫn giải

- Góc xAz và góc xAt là hai góc kề nhau.

- Góc xAy và xAt là hai góc kề nhau.

- Góc xAz và yAz là hai góc kề nhau.

- Góc zAy và tAy là hai góc kề nhau.

- Góc xAy và tAy là hai góc kề nhau.

- Góc tAy và tAx là hai góc kề nhau.

- Góc xAz và zAt là hai góc kề nhau.

- Góc xAt và zAt là hai góc kề nhau.

- Góc yAt và zAt là hai góc kề nhau.

- Góc yAz và zAt là hai góc kề nhau.

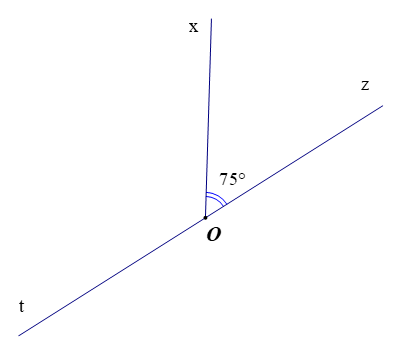
Bài 2: Biết góc xOz và xOt là hai góc kề bù. Hãy tính góc xOt.

Hướng dẫn giải

Vì góc xOz và góc xOt là hai góc kề bù nên $\widehat{xOz}+\widehat{xOt}={180}^0$.

Suy ra ${75}^0+\widehat{xOt}={180}^0$ suy ra $\widehat{xOt}={180}^0-{75}^0={105}^0$.

Vậy $\widehat{xOt}={105}^0$.

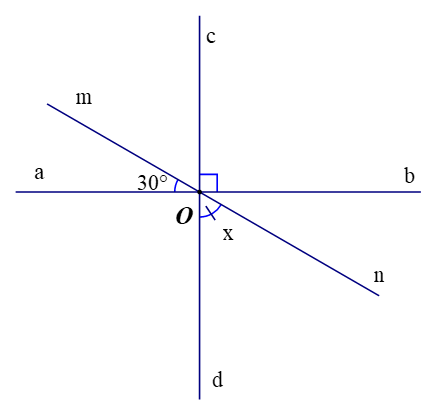
Bài 3: Tìm x trong hình vẽ

Hướng dẫn giải

Góc aOc và góc cOb kề bù, mà $\widehat{cOb}={90}^0$.

Nên $\widehat{aOc}={180}^0-\widehat{cOb}={180}^0-{90}^0={90}^0$.

Ta có góc aOm và mOc là hai góc kề nhau.

Nên $\widehat{aOc}=\widehat{aOm}+\widehat{mOc}$, mà $\widehat{aOc}={90}^0$

Suy ra: $\widehat{mOc}=\widehat{aOc}-\widehat{aOm}={90}^0-{30}^0={60}^0$.

Vì góc mOc và góc nOd đối đỉnh nên ta có $x=\widehat{nOd}=\widehat{mOc}={60}^0$.

Vậy $x={60}^0$.

Bài 4: Cho góc xOy có số đo bằng 110⁰. Tia Oz là tia phân giác của góc xOy. Tính số đo các góc xOz và yOz.

Hướng dẫn giải

Vì tia Oz là tia phân giác của góc xOy nên:

Ta có $\widehat{xOz}=\widehat{yOz}=\widehat{xOy}:2={110}^0:2={55}^0$.

Vậy $\widehat{xOz}=\widehat{yOz}={55}^0$.

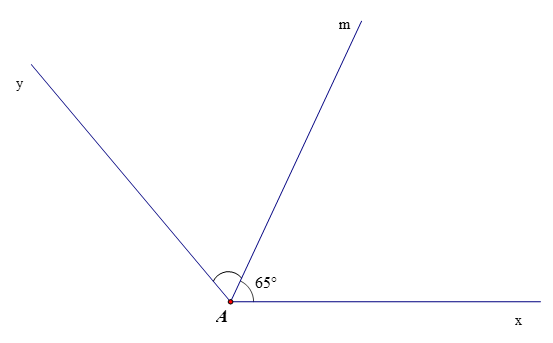
Bài 5: Cho góc xAm có số đo bằng 65⁰ và tia Am là tia phân giác của xAy. Tính số đo góc xAy.

Hướng dẫn giải

Vì Am là tia phân giác của góc xAy nên:

Ta có $\widehat{xAy}=2.\widehat{xAm}={2.65}^0={130}^0$.

Vậy $\widehat{xAy}={130}^0$.

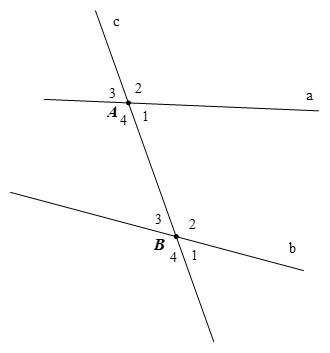
Bài 6: Hãy kể tên các cặp góc so le trong, đồng vị trong hình vẽ sau.

Hướng dẫn giải

- Các cặp góc so le trong là: A₁ và B₃; A₄ và B₂.

- Các cặp góc đồng vị là: A₁ và B₁; A₂ và B₂; A₃ và B₃; A₄ và B₄.

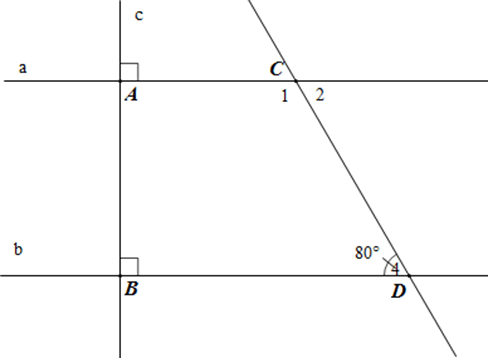
Bài 7: Cho hình vẽ sau:

a) Vì sao a // b?

b) Tính số đo các góc C₁, C₂ trong hình vẽ.

Hướng dẫn giải

a) Ta có góc A và góc B là hai góc đồng vị, mà $\hat{A}=\hat{B}={90}^0$.

Vậy nên a // b.

b) Ta có góc C₁ và D₄ là hai góc trong cùng phía.

Mà a // b nên $\widehat{C_1}+\widehat{D_4}={180}^0$

Suy ra $\widehat{C_1}={180}^0-\widehat{D_4}={180}^0-{80}^0={100}^0$.

Góc C₂ và góc D₄ ở vị trí so le trong nên $\widehat{C_2}=\widehat{D_4}={80}^0$.

Vậy $\widehat{C_1}={100}^0$; $\widehat{C_2}={80}^0$.

Bài 8: Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho định lý sau: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường còn lại”.

Hướng dẫn giải

GT	a // b c ⊥ a
KL	c ⊥ b

Bài 9: Cho định lý : “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”.

a) Vẽ hình minh họa nội dung định lý trên.

b) Viết giả thiết, kết luận của định lý trên.

c) Chứng minh định lý trên.

Hướng dẫn giải

a)

b)

GT	a // b, c cắt a tại A, c cắt b tại B $\widehat{A_1},\widehat{B_1}$ là hai góc đồng vị.
KL	$\widehat{A_1}=\widehat{B_1}$

c) Chứng minh

Qua điểm B kẻ đường thẳng b’ sao cho góc $\widehat{B_2}=\widehat{A_1}$.

Khi đó đường thẳng c tạo với hai đường thẳng a và b’ hai góc đồng vị bằng nhau.

Theo dấu hiệu nhận biết hai đường thẳng song song, ta có a và b’ song song với nhau.

Suy ra qua B có hai đường thẳng b, b’ cùng song song với a.

Theo Tiên đề Euclid thì hai đường thẳng b’ và b trùng nhau.

Từ đó suy ra $\widehat{B_1}=\widehat{A_1}$ (vì cùng bằng $\widehat{B_2}$).

Học tốt Toán 7 Chương 4

Các bài học để học tốt Chương 4 Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài tập cuối chương 4

• Giải sbt Toán 7 Bài tập cuối chương 4