Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (Lý thuyết Toán lớp 7) - Cánh diều
Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (Lý thuyết Toán lớp 7) - Cánh diều
Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
1. Trường hợp bằng nhau cạnh – cạnh –cạnh (c.c.c)
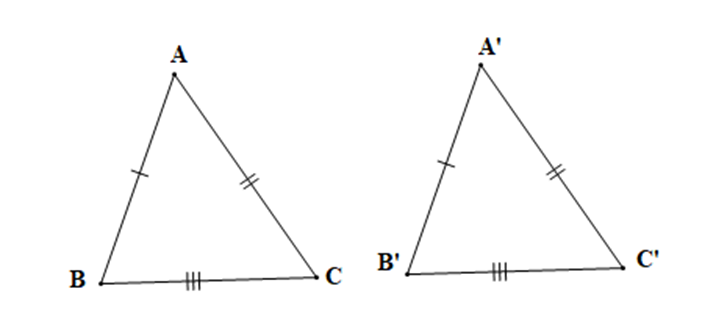
– Tính chất: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Nếu AB=A’B’, AC = A’C’, BC = B’C’ thì ∆ABC = ∆A’B’C’ (c.c.c).
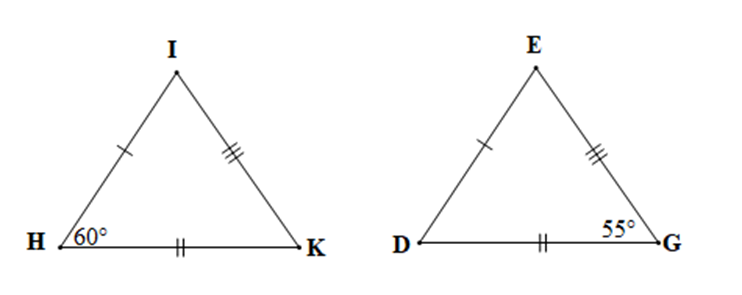
Ví dụ: Cho hai tam giác HIK và DEG thỏa mãn HI = DE, IK = EG, HK = DG.
a) Chứng minh ∆HIK = ∆DEG.
b) Biết Tính số đo góc D và góc I.
Hướng dẫn giải
a) Xét ∆HIK và ∆DEG có:
HI = DE (giả thiết),
IK = EG (giả thiết),
HK = DG (giả thiết),
Suy ra ∆HIK = ∆DEG (c.c.c).
Vậy ∆HIK = ∆DEG.
b) Vì ∆HIK = ∆DEG (theo câu a)
Suy ra (các cặp góc tương ứng)
Mà nên
Xét ∆DEG có: (tổng ba góc trong một tam giác)
Do đó
Mà
Suy ra
Lại có (chứng minh trên).
Nên
Vậy
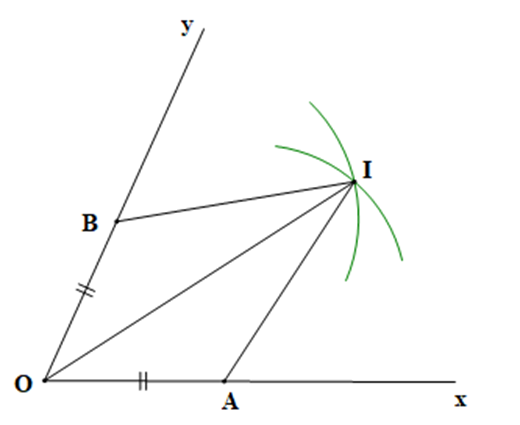
Ví dụ: Cho trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Vẽ các cung tròn tâm A và B có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong góc xOy. Chứng minh OI là tia phân giác của góc xOy.
Hướng dẫn giải
Vì các cung tròn tâm A và tâm B có cùng bán kính cắt nhau ở điểm I nằm trong góc xOy (giả thiết) nên ta có AI = BI
Xét tam giác OAI và tam giác OBI có:
OA = OB (giả thiết),
AI = BI (chứng minh trên),
OI là cạnh chung.
Suy ra ∆OAI = ∆OBI (c.c.c).
Do đó (hai góc tương ứng)
Nên tia OI là tia phân giác của góc xOy.
Vậy tia OI là tia phân giác của góc xOy.
– Nhận xét: Cách vẽ tia phân giác của một góc đã được chứng minh cụ thể như trên.
2. Áp dụng vào trường hợp bằng nhau về cạnh huyền và cạnh góc vuông của tam giác vuông
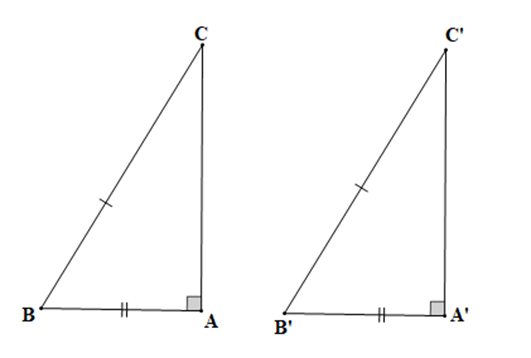
– Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Hai tam giác ABC và A’B’C’ có BC = B’C’, AB=A’B’ thì ∆ABC = ∆A’B’C’ (cạnh huyền – cạnh góc vuông).
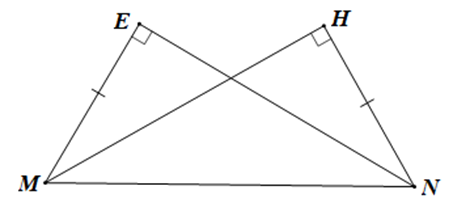
Ví dụ: Cho hình vẽ sau:
a) Chứng minh
b) Biết Chứng minh MH là tia phân giác của
Hướng dẫn giải
a) Xét ∆EMN và ∆HNM có:
ME = HN (giả thiết),
MN là cạnh chung,
Suy ra ∆EMN = ∆HNM (cạnh huyền – cạnh góc vuông).
Do đó (hai góc tương ứng).
Vậy
b) Xét ∆EMN vuông tại E có: (tổng hai góc nhọn trong tam giác vuông bằng 90°).
Suy ra
Mà (chứng minh trên)
Do đó
Mặt khác và là hai góc kề nhau nên ta có:
Suy ra
Do đó
Suy ra MH là tia phân giác của
Vậy MH là tia phân giác của
3. Vẽ tam giác khi biết ba cạnh
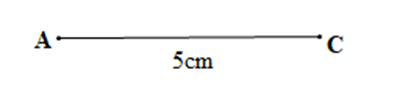
Ví dụ: Để vẽ tam giác ABC có AB = 3 cm, AC = 5 cm, BC = 7 cm bằng thước thẳng (có chia đơn vị) và compa, ta làm như sau:
–Bước 1: Vẽ đoạn thẳng AC = 5 cm
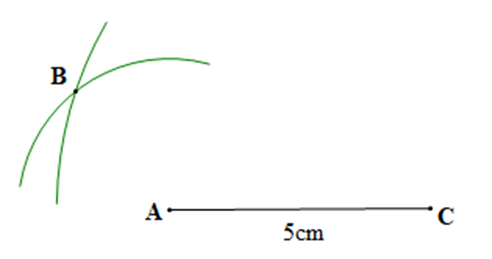
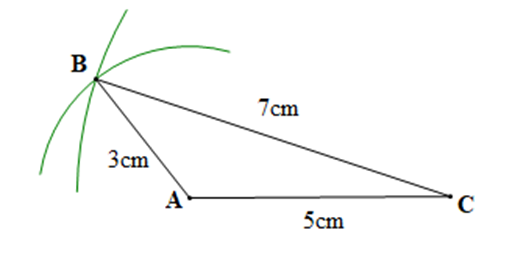
– Bước 2: Vẽ một phần đường tròn tâm A bán kính 3 cm và một phần đương tròn tâm C bán kính 7 cm, B là điểm chung của hai phần đường tròn đó
– Bước 3: Vẽ các đoạn thẳng AB, BC. Ta được tam giác ABC.
Bài tập Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
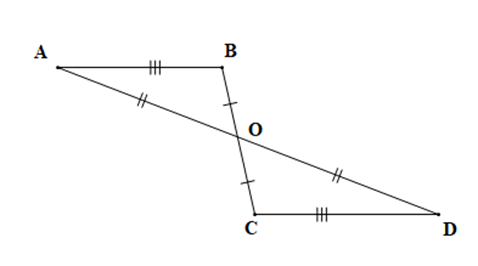
Bài 1. Cho hình vẽ:
Chứng minh AB // CD.
Hướng dẫn giải
Xét ∆OAB và ∆ODC có:
AB = DC (giả thiết),
OB = OC (giả thiết),
OA = OD (giả thiết),
Suy ra ∆OAB = ∆ODC (c.c.c)
Do đó (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong của AB và CD.
Nên AB // CD (dấu hiệu nhận biết).
Vậy AB // CD.
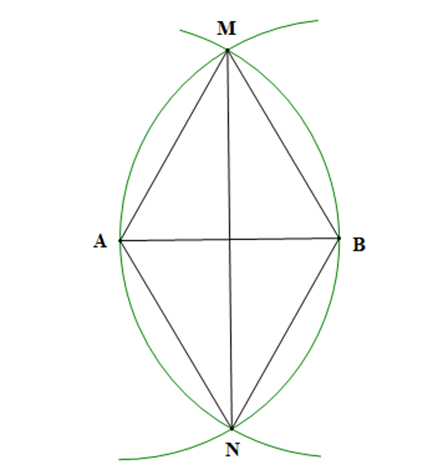
Bài 2. Cho đoạn thẳng AB. Vẽ cung tròn tâm A bán kính AB, vẽ cung tròn tâm B bán kính BA, chúng cắt nhau tại hai điểm M và N. Chứng minh ∆ABM = ∆ABN và ∆AMN = ∆BMN.
Hướng dẫn giải
Vì cung tròn tâm A bán kính AB cắt cung tròn tâm B bán kính BA tại hai điểm M và N nên AM = AN = BM = BN = AB.
+) Xét ∆MAB và ∆NAB có:
AB là cạnh chung,
MA = NA (chứng minh trên),
MB = NB (chứng minh trên),
Suy ra ∆MAB = ∆NAB (c.c.c).
+) Xét ∆AMN và ∆BMN có:
MN là cạnh chung,
MA = MB (chứng minh trên),
AN = NB (chứng minh trên),
Suy ra ∆AMN = ∆BMN (c.c.c)
Vậy ∆ABM = ∆ABN và ∆AMN = ∆BMN.
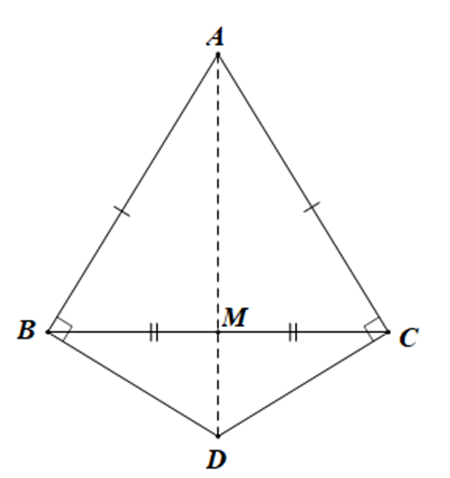
Bài 3. Cho tam giác ABC có AB = AC. Đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AC tại C cắt nhau tại điểm D.
a) Chứng minh ∆ABD = ∆ACD.
b) Gọi M là trung điểm của BC. Chứng minh A, M, D thẳng hàng.
Hướng dẫn giải
a) Vì AB ⊥ BD tại B nên
Vì AC ⊥ CD tại C nên
Xét ∆ABD và ∆ACD có:
AD là cạnh chung,
AB = AC (giả thiết),
Do đó ∆ABD = ∆ACD (cạnh huyền – cạnh góc vuông).
Vậy ∆ABD = ∆ACD.
b) Vì M là trung điểm của BC nên MB = MC.
Xét ∆ABM và ∆ACM có:
AB = AC (giả thiết),
AM là cạnh chung,
MB = MC (chứng minh trên).
Do đó ∆ABM = ∆ACM (c.c.c)
Suy ra (hai góc tương ứng)
Mà (hai góc kề bù)
Do đó
Chứng minh tương tự ta cũng có:
∆DBM = ∆DCM (c.c.c)
Suy ra (hai góc tương ứng)
Mà (hai góc kề bù)
Do đó
Ta có: và
Suy ra
Do đó và là hai góc kề bù.
Nên ba điểm A, M, D cùng nằm trên một đường thẳng.
Vậy ba điểm A, M, D thẳng hàng.
Học tốt Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
Các bài học để học tốt Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh Toán lớp 7 hay khác: