Hai tam giác bằng nhau (Lý thuyết Toán lớp 7) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 3: Hai tam giác bằng nhau hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Hai tam giác bằng nhau (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Hai tam giác bằng nhau

– Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

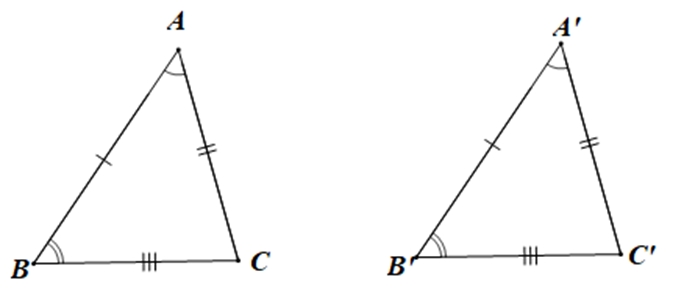
Ví dụ: Cho hai tam giác ABC và A’B’C’ như hình vẽ dưới đây:

Hai tam giác này có bằng nhau không? Vì sao?

Hướng dẫn giải

Xét tam giác ABC và tam giác A'B'C' có:

+) AB = A'B', AC = A'C', BC = B'C';

+) $\hat{A}=\widehat{A^{\text{'}}},\hat{B}=\widehat{B^{\text{'}}},\hat{C}=\widehat{C^{\text{'}}}.$

Do đó hai tam giác ABC và A’B’C’ là hai tam giác bằng nhau.

– Khi tam giác ABC và tam giác A'B'C' bằng nhau thì ta kí hiệu là: ∆ABC = ∆A'B'C'.

– Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.

- Chú ý:

+ Nếu AB=A'B', AC = A'C', BC = B'C' và $\hat{A}=\widehat{A^{\text{'}}},\hat{B}=\widehat{B^{\text{'}}},\hat{C}=\widehat{C^{\text{'}}}$ thì ∆ABC = ∆A'B'C'.

+ Nếu ∆ABC = ∆A'B'C' thì AB=A'B', AC = A'C', BC = B'C' và $\hat{A}=\widehat{A^{\text{'}}},$ $\hat{B}=\widehat{B^{\text{'}}},$$\hat{C}=\widehat{C^{\text{'}}}.$

Ở đây:

• Hai góc A và A' (B và B', C và C') là hai góc tương ứng;

• Hai cạnh AB và A'B' (BC và B'C', AC và A'C') là hai cạnh tương ứng.

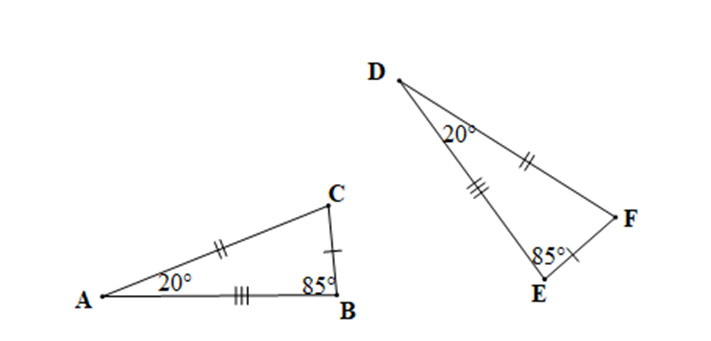
Ví dụ: Cho hai tam giác ABC và DEF như hình vẽ dưới đây:

Hai tam giác ABC và DEF có bằng nhau không? Nếu bằng nhau hãy viết kí hiệu bằng nhau của hai tam giác đó.

Hướng dẫn giải

Xét tam giác FDE có $\hat{F}+\hat{D}+\hat{E}=180°$(định lí tổng ba góc trong một tam giác)

Suy ra $\hat{F}=180°-\hat{E}-\hat{D}$

Hay $\hat{F}=180°-85°-20°=75°$

Xét tam giác BCA ta cũng có:$\hat{B}+\hat{C}+\hat{A}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{C}=180°-\hat{B}-\hat{A}$

Hay $\hat{C}=180°-85°-30°=75°$

Xét tam giác FDE và tam giác BCA có:

+) AB = DE, AC = DF, BC = EF

+) $\hat{A}=\hat{D}\left(=20°\right),\hat{B}=\hat{E}\left(=85°\right),\hat{C}=\hat{F}\left(=75°\right)$

Do đó ∆ABC = ∆DEF.

Bài tập Hai tam giác bằng nhau

Bài 1. Cho biết DABC = DMNP, AB = 4 cm, AC = 3 cm, NP = 5 cm.

a) Tính độ dài các cạnh BC, MP, NM.

b) Tính chu vi tam giác ABC.

c) So sánh $\hat{P}$ và $\hat{N}.$

Hướng dẫn giải

Vì ∆ABC = ∆MNP nên ta có:

AB = MN, AC = MP, BC = NP(các cặp cạnh tương ứng)

Mà AB = 4 cm, AC = 3 cm, NP = 5 cm

Do đó MN = 4cm, MP = 3 cm, BC = 5 cm.

Vậy MN = 4cm, MP = 3 cm, BC = 5 cm.

b) Chu vi tam giác ABC là:

AB + BC + CA = 4 + 5 + 3 = 12 (cm).

Vậy chu vi tam giác ABC bằng 12 cm.

c) Xét tam giác MNP có:

• Cạnh MN đối diện với $\hat{P};$

• Cạnh MP đối diện với $\hat{N};$

• MN > MP

Do đó $\hat{P}>\hat{N}$ (quan hệ giữa cạnh và góc đối diện)

Vậy $\hat{P}>\hat{N}$

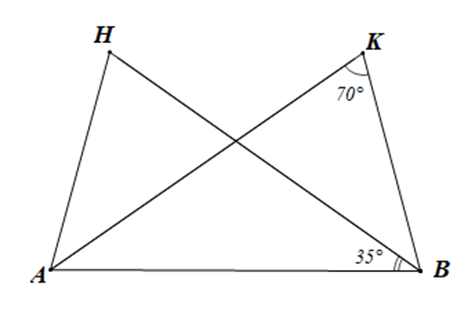
Bài 2. Cho hình vẽ:

Biết ∆ABH = ∆BAK, tính số đo góc ABK.

Hướng dẫn giải

Vì ∆ABH = ∆BAK nên $\widehat{HAB}=\widehat{KBA}\widehat{,HBA}=\widehat{K\text{A}B}$ (các cặp góc tương ứng)

Mà $\widehat{HBA}=35°$

Suy ra $\widehat{K\text{A}B}=35°.$

Xét tam giác ABK có $\hat{K}+\widehat{K\text{A}B}+\widehat{KBA}=180°$(tổng ba góc trong một tam giác)

Suy ra $\widehat{ABK}=180°-\widehat{K\text{A}B}-\hat{K}$

Hay $\widehat{ABK}=180°-35°-70°=75°$

Vậy số đo góc ABK là 75°.

Bài 3. Cho ∆ABC = ∆A’B’C’. Biết $\hat{A}:\hat{B}:\hat{C}=3:4:5.$ Tính các góc của tam giác A’B’C’.

Hướng dẫn giải

Xét tam giác ABC có $\hat{A}+\hat{B}+\hat{C}=180°$(tổng ba góc trong một tam giác)

Theo bài $\hat{A}:\hat{B}:\hat{C}=3:4:5$

Suy ra $\frac{\hat{A}}{3}=\frac{\hat{B}}{4}=\frac{\hat{C}}{5}$

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{\hat{A}}{3}=\frac{\hat{B}}{4}=\frac{\hat{C}}{5}=\frac{\hat{A}+\hat{B}+\hat{C}}{3+4+5}=\frac{180°}{12}=15°$

Khi đó:

• $\frac{\hat{A}}{3}=15°$ suy ra $\hat{A}=15°.3=45°;$

• $\frac{\hat{B}}{4}=15°$ suy ra $\hat{B}=15°.4=60°;$

• $\frac{\hat{C}}{5}=15°$ suy ra $\hat{C}=15°.5=75°.$

Vì ∆ABC = ∆A’B’C’ nên ta có:

$\hat{A}=\widehat{A^{\text{'}}}=45°;\hat{B}=\widehat{B^{\text{'}}}=60°$ và $\hat{C}=\widehat{C^{\text{'}}}=75°$(các cặp góc tương ứng)

Vậy $\widehat{A^{\text{'}}}=45°,\widehat{B^{\text{'}}}=60°$ và $\widehat{C^{\text{'}}}=75°.$

Học tốt Hai tam giác bằng nhau

Các bài học để học tốt Hai tam giác bằng nhau Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 3: Hai tam giác bằng nhau

• Giải sbt Toán 7 Bài 3: Hai tam giác bằng nhau