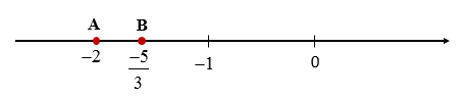Tập hợp ℚ các số hữu tỉ (Lý thuyết Toán lớp 7) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 7 Bài 1: Tập hợp Q các số hữu tỉ hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tập hợp ℚ các số hữu tỉ (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Tập hợp Q các số hữu tỉ

1. Số hữu tỉ

- Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}$ (a, b ∈ ℤ, b ≠ 0).

- Tập hợp các số hữu tỉ kí hiệu là ℚ.

Ví dụ: Các số -7; 0,6; -1,2; 1$\frac{4}{5}$ là các số hữu tỉ bởi vì chúng đều viết được dưới dạng phân số: $-7=\frac{-7}{1}\text{; 0,6=}\frac{6}{10};-\text{1,2=}\frac{-12}{10};\text{ 1}\frac{4}{5}=\frac{9}{5}$.

Chú ý:

- Mỗi số nguyên là một số hữu tỉ.

- Các phân số bằng nhau là cách viết khác nhau của cùng một số hữu tỉ.

Ví dụ: Vì $\frac{1}{2}=\frac{2}{4}$ nên $\frac{1}{2}$ và $\frac{2}{4}$ cùng biểu diễn một số hữu tỉ.

2. Biểu diễn số hữu tỉ trên trục số

- Tương tự số nguyên ta có thể biểu diễn mọi số hữu tỉ trên trục số.

- Điểm biểu diễn số hữu tỉ a được gọi là điểm a.

- Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số ta chọn một trong những phân số đó để biểu diễn. Thông thường ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.

- Nếu số hữu tỉ chưa viết dưới dạng phân số thì ta viết lại chúng dưới dạng phân số rồi biểu diễn phân số đó trên trục số.

Ví dụ: a) Biểu diễn số hữu tỉ 1,5 trên trục số.

- Ta viết 1,5 dưới dạng phân số: $1,5=\frac{15}{10}=\frac{3}{2}$. Ta sẽ biểu diễn phân số $\frac{3}{2}$ trên trục số.

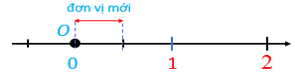
- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành hai phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ).

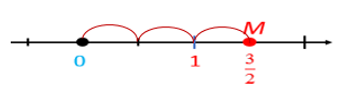
- Đi theo chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm M. Điểm M biểu diễn số hữu tỉ $\frac{3}{2}$ , và cũng chính là điểm biểu diễn số hữu tỉ 1,5 và $\frac{15}{10}$ .

b) Biểu diễn số hữu tỉ $\frac{-3}{2}$trên trục số.

- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành hai phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ).

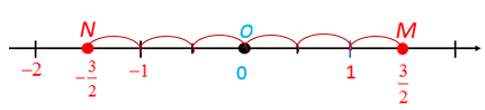
- Đi theo chiều ngược chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm N. Điểm N biểu diễn số hữu tỉ $\frac{-3}{2}$ .

Nhận xét: Vì $-\frac{3}{2}=\frac{-3}{2}=\frac{3}{-2}$nên điểm N biểu diễn số $\frac{-3}{2}$ cũng là điểm biểu diễn số $-\frac{3}{2}$và $\frac{3}{-2}$ .

3. Số đối của một số hữu tỉ

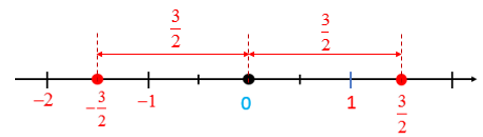
- Trên trục số hai số hữu tỉ phân biệt có điểm biểu diễn nằm về hai phía của điểm gốc O và cách đều điểm gốc O được gọi là hai số đối nhau.

- Số đối của số hữu tỉ a, kí hiệu là –a.

- Số đối của số 0 là 0.

Ví dụ:

- Số đối của số $\frac{3}{2}$ là số $-\frac{3}{2}$

- Số đối của số $\frac{-2}{7}$ là số $-\left(\frac{-2}{7}\right)=\frac{2}{7}$ .

4. So sánh các số hữu tỉ

4.1 So sánh hai số hữu tỉ

Trong hai số hữu tỉ khác nhau bao giờ cũng có một số nhỏ hơn số kia.

- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.

- Số hữu tỉ 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương

- Nếu a < b và b < c thì a < c.

4.2 Cách so sánh hai số hữu tỉ

+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta dùng quy tắc đã học ở lớp 6 để so sánh.

+ Các trường hợp khác hai trường hợp trên, để so sánh hai số hữu tỉ ta viết chúng cùng về dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.

Ví dụ:

a) So sánh $-\frac{1}{3}$ và $\frac{-2}{5}$

Hai phân số trên cùng là phân số, vì vậy ta sẽ áp dụng quy tắc so sánh hai phân số đã học.

Ta quy đồng để đưa hai phân số về cùng mẫu số dương

$-\frac{1}{3}=\frac{-1}{3}=\frac{(-1)\cdot 5}{3\cdot 5}=\frac{-5}{15}$; $\frac{-2}{5}=\frac{(-2)\cdot 3}{5\cdot 3}=\frac{-6}{15}$

Vì $-5>-6$ nên $\frac{-5}{15}>\frac{-6}{15}$ . Suy ra $-\frac{1}{3}>\frac{-2}{5}$ .

b) So sánh 1,206 và 1,3

Hai số trên cùng là số thập phân, vì vậy ta sẽ áp dụng quy tắc so sánh hai số thập phân.

Ta so sánh phần nguyên với nhau, khi phần nguyên bằng nhau ta sẽ so sánh đến phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn…

1,206 < 1,3 (vì phần nguyên bằng nhau, hàng phần mười có 2 < 3).

c) So sánh –0,3 và $\frac{-2}{7}$

Ta thấy hai số trên chưa cùng là phân số hoặc số thập phân, vì vậy ta đưa chúng về cùng là phân số hoặc số thập phân sau đó so sánh chúng.

Ta có $-0,3=\frac{-3}{10}$, ta sẽ áp dụng quy tắc so sánh hai phân số $\frac{-3}{10}$ và $\frac{-2}{7}$

Ta có : $\frac{-3}{10}=\frac{(-3)\cdot 7}{10\cdot 7}=\frac{-21}{70}$; $\frac{-2}{7}=\frac{(-2)\cdot 10}{7\cdot 10}=\frac{-20}{70}$

Vì – 21 < –20 nên $\frac{-21}{70}<\frac{-20}{70}$ . Suy ra – 0,3 < $\frac{-2}{7}$

4.3 Minh họa trên trục số

Hai điểm x, y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số :

- Trên trục số nằm ngang: Nếu x < y hay y > x thì điểm x nằm bên trái điểm y.

- Trên trục số thẳng đứng: Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y.

Ví dụ : So sánh hai số: – 2 và $\frac{-5}{3}$

Ta có : $-2=\frac{-2}{1}=\frac{-6}{3}$ mà $\frac{-6}{3}<\frac{-5}{3}$ vậy nên $-2<\frac{-5}{3}$ .

Trên trục số nằm ngang điểm – 2 nằm bên trái điểm $\frac{-5}{3}$ .

Bài tập Tập hợp Q các số hữu tỉ

Bài 1. Các số: $-1,25;\text{0; 2}\frac{5}{7};$ có là số hữu tỉ không? Vì sao?

Hướng dẫn giải

Các số $-1,25;\text{0; 2}\frac{5}{7};$ đều là số hữu tỉ, vì vậy chúng viết được dưới dạng phân số: $-1,25=\frac{-125}{100};\text{0=}\frac{0}{1}\text{; 2}\frac{5}{7}\text{=}\frac{19}{7}$ .

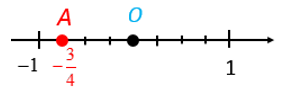
Bài 2. Hãy biểu diễn số hữu tỉ $-\frac{3}{4}$ trên trục số.

Hướng dẫn giải

- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành bốn phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ).

- Đi theo chiều ngược chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm A. Điểm A chính là điểm biểu diễn số hữu tỉ $-\frac{3}{4}$ .

Bài 3. Tìm số đối của số hữu tỉ $\frac{3}{-5}$ .

Hướng dẫn giải

Số đối của số hữu tỉ $\frac{3}{-5}$ là: $-\left(\frac{3}{-5}\right)=-\left(-\frac{3}{5}\right)=\frac{3}{5}$ .

Bài 4. So sánh hai số hữu tỉ $\frac{2}{-7}$ và $\frac{-3}{11}$ .

Hướng dẫn giải

Hai số hữu tỉ trên đã viết dưới dạng phân số vì vậy để so sánh ta đưa phân số về có cùng mẫu dương, sau đó ta chỉ cần so sánh hai tử số.

Ta có $\frac{2}{-7}=\frac{-2}{7}=\frac{-22}{77}$ và $\frac{-3}{11}=\frac{-21}{77}$

Vì -22 < -21 nên $\frac{-22}{77}<\frac{-21}{77}$. Suy ra $\frac{2}{-7}<\frac{-3}{11}$.

Học tốt Tập hợp Q các số hữu tỉ

Các bài học để học tốt Tập hợp Q các số hữu tỉ Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ