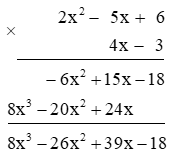Phép nhân đa thức một biến (Lý thuyết Toán lớp 7) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 4: Phép nhân đa thức một biến hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Phép nhân đa thức một biến (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Phép nhân đa thức một biến

1. Nhân đơn thức với đơn thức

– Muốn nhân đơn thức A với đơn thức B, ta làm như sau:

+ Nhân hệ số của đơn thức A với hệ số của đơn thức B;

+ Nhân luỹ thừa của biến A với luỹ thừa của biến đó trong B;

+ Nhân các kết quả vừa tìm được với nhau.

– Tổng quát: Với a ≠ 0, b ≠ 0; m, n ∈ℕ ta có:

ax^m. bxⁿ = a.b. x^m. xⁿ = abx^{m + n}.

Ví dụ: Tính:

a) 3x². 5x⁶;

b) – 4x³. 4x²;

c) 2x^{m + 2}. x^{n – 2} (m, n ∈ℕ, n > 2).

Hướng dẫn giải

a) 3x². 5x⁶ = 3.5. x². x⁶ = 15x^{2 + 6} = 15x⁸;

b) – 4x³. 4x² = – 4.4. x³. x² = –16x^{3 + 2} = –16x⁵;

c) 2x^{m + 2}. x^{n – 2} = 2. x^{m + 2}. x^{n – 2} = 2x^{m + 2 + n – 2} = 2x^{m + n}.

2. Nhân đơn thức với đa thức

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng đơn thức của đa thức rồi cộng các tích với nhau.

A(B + C) = AB + AC

A(B – C) = AB – AC

Ví dụ: Tính:

a) x(2x + 1);

b) –2x²(2x² + 2x – 1);

c) –2x³($\frac{1}{2}$x² + 3x – 5).

Hướng dẫn giải

a) x(2x + 1) = x.2x + x.1 = 2x² + x;

b) –2x²(2x² + 2x – 1)

= –2x².2x² –2x².2x –2x².(–1)

= –4x⁴ – 4x³ + 2x²;

c) –2x³($\frac{1}{2}$x² + 3x – 5)

= –2x³.$\frac{1}{2}$x² –2x³.3x – 2x³.(–5)

= –x⁵ – 6x⁴ + 10x³.

3. Nhân đa thức với đa thức

– Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.

(A + B)(C + D) = AC + AD + BC + BD

– Tích của hai đa thức là một đa thức.

– Sau khi thực hiện phép nhân hai đa thức, ta thường viết đa thức tích ở dạng thu gọn và sắp xếp các đơn thức theo số mũ tăng dần hoặc giảm dần của biến.

Ví dụ: Thực hiện phép nhân (4x – 3)(2x² – 5x + 6).

Hướng dẫn giải

Ta có: (4x – 3)(2x² – 5x + 6)

= 4x(2x² – 5x + 6) – 3(2x² – 5x + 6)

= 4x.2x² – 4x.5x + 4x.6 – 3.2x² – 3.(–5x) – 3.6

= 8x³ – 20x² + 24x – 6x² + 15x – 18

= 8x³ – 26x² + 39x – 18

Vậy (4x – 3)(2x² – 5x + 6) = 8x³ – 26x² + 39x – 18.

– Chúng ta có thể trình bày phép nhân đa thức theo cột dọc.

Chú ý: Khi thực hiện phép nhân hai đa thức theo cột dọc, các đơn thức có cùng số mũ (của biến) được xếp vào cùng một cột.

Ví dụ: Thực hiện phép nhân (4x – 3)(2x² – 5x + 6) theo cột dọc.

Hướng dẫn giải

Ta có: (4x – 3)(2x² – 5x + 6) = (2x² – 5x + 6).(4x – 3)

Thực hiện phép nhân theo cột dọc như sau:

Vậy (4x – 3)(2x² – 5x + 6) = 8x³ – 26x² + 39x – 18.

Bài tập Phép nhân đa thức một biến

Bài 1. Thực hiện phép tính:

a) $\frac{3}{2}$x⁵. 4x²;

b) y²(0,5y³ + 2y² – y + 0,25);

c) (x² + 2x + 1)(x² – x – 1);

d) (2x – 3)(3x + 1) – (x + 2)(6x – 1).

Hướng dẫn giải

a) $\frac{3}{2}$x⁵. 4x² = $\frac{3}{2}$.4. x⁵.x² = 6x⁷.

b) y²(0,5y³ + 2y² – y + 0,25)

= y².0,5y³ + y².2y² – y².y + y².0,25

= 0,5y⁵ + 2y⁴ – y³ + 0,25y²

c) (x² + 2x + 1)(x² – x – 1)

= (x².x² – x².x – x².1) + (2x.x² – 2x.x – 2x.1) + (1.x² – 1.x – 1.1)

= x⁴ – x³ – x² + 2x³ – 2x² – 2x + x² – x – 1

= x⁴ + (– x³ + 2x³) + (– x² – 2x² + x²) + (– 2x – x) – 1

= x⁴ + x³ – 2x² – 3x – 1

d) (2x – 3)(3x + 1) – (x + 2)(6x – 1)

= 2x.3x + 2x.1 – 3.3x – 3.1 – [x.6x – x.1 + 2.6x + 2.(–1)]

= 6x² + 2x – 9x – 3 – 6x² + x – 12x + 2

= (6x² – 6x²) + (2x – 9x + x – 12x) + (– 3 +2)

= –18x – 1.

Bài 2. Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau:

a) A(x) = (x² – x + 1)(x + 1)

b) B(x) = (x³ + x² – 1)(3x³ – x)

Hướng dẫn giải

a) A(x) = (x² – x + 1)(x + 1)

= x².x + x².1 – x.x – x.1 + 1.x + 1.1

= x³ + x² – x² – x + x + 1

= x³ + 1

Bậc của A(x) là 3, hệ số cao nhất là 1, hệ số tự do là 1.

b) B(x) = (x³ + x² – 1)(3x³ – x)

= x³.3x³ – x³.x + x².3x³ – x².x – 1.3x³ + 1.x

= 3x⁶ – x⁴ + 3x⁵ – x³ – 3x³ + x

= 3x⁶ + 3x⁵ – x⁴ – 4x³ + x

Bậc của B(x) là 6, hệ số cao nhất là 3, hệ số tự do là 0.

Bài 3. Cho đa thức P(x) = x²(x² – x – 1) + 3x(x + a) + 2, với a là một số.

a) Thu gọn đa thức P(x) rồi sắp xếp đa thức theo số mũ giảm dần của biến.

b) Tìm a sao cho tổng các hệ số của đa thức P(x) bằng 10.

Hướng dẫn giải

a) P(x) = x²(x² – x – 1) + 3x(x + a) + 2

= x².x² – x².x – x².1 + 3x.x + 3x.a + 2

= x⁴ – x³ – x² + 3x² + 3ax + 2

= x⁴ – x³ + 2x² + 3ax + 2

Vậy P(x) = x⁴ – x³ + 2x² + 3ax + 2.

b) Ta có P(x) = x⁴ – x³ + 2x² + 3ax + 2.

Hệ số của x⁴ là 1;

Hệ số của x³ là –1;

Hệ số của x² là 2;

Hệ số của x là 3a;

Hệ số tự do là 2.

Tổng các hệ số của P(x) là:

1 + (–1) + 2 + 3a + 2 = 3a + 4.

Mà theo bài tổng các hệ số của đa thức P(x) bằng 10.

Khi đó: 3a + 4 = 10

Do đó 3a = 6

Vậy a = 2.

Bài 4. Một hình hộp chữ nhật có chiều dài đáy là x + 3 (cm), chiều rộng đáy nhỏ hơn chiều dài đáy 5 cm và chiều cao là x + 2 (cm). Tính thể tích hình hộp chữ nhật đó.

Hướng dẫn giải

Chiều rộng hình hộp chữ nhật là: x + 3 – 5 = x – 2 (cm).

Thể tích hình hộp chữ nhật là:

V = (x + 3)(x – 2)(x + 2)

= (x.x – 2.x + 3.x – 3.2)(x + 2)

= (x² + x – 6)(x + 2)

= x².x + x².2 + x.x + x.2 – 6.x – 6.2

= x³ + 2x² + x² + 2x – 6x – 12

= x³ + 3x² – 4x – 12

Vậy thể tích hình hộp chữ nhật là: x³ + 3x² – 4x – 12 (cm³).

Học tốt Phép nhân đa thức một biến

Các bài học để học tốt Phép nhân đa thức một biến Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 4: Phép nhân đa thức một biến

• Giải sbt Toán 7 Bài 4: Phép nhân đa thức một biến