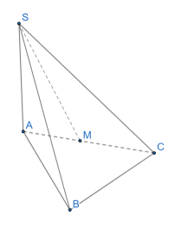
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông cân tại B

Giải sách bài tập Toán 12 Bài tập ôn tập cuối năm - Kết nối tri thức

Bài 12 trang 50 SBT Toán 12 Tập 2: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông cân tại B, biết SA = AB = BC = a. Gọi M là trung điểm của cạnh AC. Tính tích vô hướng $\overrightarrow{\mathrm{S}\mathrm{M}}.\overrightarrow{\mathrm{B}\mathrm{C}}$ bằng

A. $\frac{{\mathrm{a}}^2}{2}$ .

B. a².

C. −a².

D. $-\frac{{\mathrm{a}}^2}{2}$ .

Lời giải:

Đáp án đúng là: A

Tam giác ABC vuông tại B và có AB = BC nên tam giác BAC vuông cân tại B.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại B, ta có:

BA² + BC² = AC² ⇒ AC = $\sqrt{\mathrm{B}{\mathrm{A}}^2+\mathrm{B}{\mathrm{C}}^2}$  = $\mathrm{a}\sqrt{2}$

Ta có: $\overrightarrow{\mathrm{S}\mathrm{M}}.\overrightarrow{\mathrm{B}\mathrm{C}}$  = $\left(\overrightarrow{\mathrm{S}\mathrm{A}}+\overrightarrow{\mathrm{A}\mathrm{M}}\right)\overrightarrow{\mathrm{B}\mathrm{C}}=\overrightarrow{\mathrm{A}\mathrm{M}}.\overrightarrow{\mathrm{B}\mathrm{C}}=\frac{1}{2}.\overrightarrow{\mathrm{A}\mathrm{C}}.\overrightarrow{\mathrm{B}\mathrm{C}}$

= $\frac{1}{2}$ . $\mathrm{a}\sqrt{2}$.a.cos45° = $\frac{{\mathrm{a}}^2}{2}$ .

Lời giải Sách bài tập Toán lớp 12 Bài tập ôn tập cuối năm hay khác:

• Bài 1 trang 47 SBT Toán 12 Tập 2: Giá trị của tham số m để hàm số y = $\frac{1}{3}$ x³ – mx² + 4x – 2023 đạt cực trị tại x = −2 là ....

• Bài 2 trang 48 SBT Toán 12 Tập 2: Cho hàm số y = x³ + 3x² + 1 có đồ thị (C). Xét đường thẳng đi qua điểm A(−3; 1) ....

• Bài 3 trang 48 SBT Toán 12 Tập 2: Đồ thị trong hình vẽ dưới đây là của hàm số nào? ....

• Bài 4 trang 48 SBT Toán 12 Tập 2: Tất cả các giá trị thực của tham số m để đường thẳng y = x + m – 1 cắt đồ thị hàm số y ....

• Bài 5 trang 48 SBT Toán 12 Tập 2: Cho hàm số y = $\frac{{\mathrm{x}}^2-2\mathrm{x}+1}{\mathrm{x}+1}$ có đồ thị (C). Khẳng định nào sau đây là sai? ....

• Bài 6 trang 49 SBT Toán 12 Tập 2: Cho f(x) là một hàm số liên tục trên đoạn [a; b] và F(x) là một nguyên hàm của f(x) trên [a; b] ....

• Bài 7 trang 49 SBT Toán 12 Tập 2: Phát biểu nào sau đây là sai? A. $\int \mathrm{d}\mathrm{x}$ = x + C; B. $\int {\mathrm{x}}^3\mathrm{d}\mathrm{x}=\frac{1}{4}{\mathrm{x}}^4$ + C ....

• Bài 8 trang 49 SBT Toán 12 Tập 2: Nguyên hàm F(x) của hàm số f(x) = 4x³ + 2x – 1 thỏa mãn F(1) = 10 ....

• Bài 9 trang 49 SBT Toán 12 Tập 2: Cho $\underset{0}{\overset{4}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=5$ và $\underset{0}{\overset{4}{\int }}\mathrm{g}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}=6$. Giá trị của $\underset{0}{\overset{4}{\int }}\left[\mathrm{f}\left(\mathrm{x}\right)+2\mathrm{g}\left(\mathrm{x}\right)\right]\mathrm{d}\mathrm{x}$ là ....

• Bài 10 trang 49 SBT Toán 12 Tập 2: Tích phân $\mathrm{\pi }\underset{1}{\overset{3}{\int }}{\left(\mathrm{x}-1\right)}^2\mathrm{d}\mathrm{x}$ dùng để tính một trong các đại lượng sau, đó là đại lượng nào? ....

• Bài 11 trang 50 SBT Toán 12 Tập 2: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = x2 + 2, y = 3x ....

• Bài 13 trang 50 SBT Toán 12 Tập 2: Cho hình hộp ABCD.A'B'C'D', gọi G là trọng tâm của tam giác ADA' và M là trung điểm ....

• Bài 14 trang 50 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho đường thẳng ∆: $\frac{\mathrm{x}-3}{2}=\frac{\mathrm{y}+1}{1}=\frac{\mathrm{z}+4}{-3}$ ....

• Bài 15 trang 50 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho điểm A(2; −1; −3) và mặt phẳng (P): 2x – 2y – z = 0 ....

• Bài 16 trang 50 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho mặt cầu (S): x² + y² + z² – 2x – 4y + 6z + 9 = 0 ....

• Bài 17 trang 51 SBT Toán 12 Tập 2: Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư ....

• Bài 18 trang 51 SBT Toán 12 Tập 2: Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư ....

• Bài 19 trang 51 SBT Toán 12 Tập 2: Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư ....

• Bài 20 trang 51 SBT Toán 12 Tập 2: Chọn ngẫu nhiên một lá bài từ cỗ bài tú lơ khơ gồm 52 lá bài. Xác suất để lá bài lấy ra có chất rô ....

• Bài 21 trang 51 SBT Toán 12 Tập 2: Chọn ngẫu nhiên gia đình có 2 con. Biết rằng người con đầu là con gái ....

• Bài 22 trang 51 SBT Toán 12 Tập 2: Giao hai con xúc xắc cân đối, đồng chất. Biết rằng số chấm trên hai con xúc xắc bé hơn 5 ....

• Bài 23 trang 51 SBT Toán 12 Tập 2: a) Khảo sát sự biến thiên và vẽ đồ thị hàm số y = −x³ + 3x² – 2 ....

• Bài 24 trang 51 SBT Toán 12 Tập 2: a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số y = $\frac{2\mathrm{x}-1}{\mathrm{x}-1}$ ....

• Bài 25 trang 52 SBT Toán 12 Tập 2: a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = $-\frac{{\mathrm{x}}^2+\mathrm{x}+1}{\mathrm{x}}$ ....

• Bài 26 trang 52 SBT Toán 12 Tập 2: a) Lập bảng biến thiên của hàm số y = $\frac{{\mathrm{x}}^2}{\mathrm{x}+1}$; b) Tìm giá trị lớn nhất ....

• Bài 27 trang 52 SBT Toán 12 Tập 2: Một hình chóp tứ giác đều ngoại tiếp hình cầu bán kính R ....

• Bài 28 trang 52 SBT Toán 12 Tập 2: Tìm học các nguyên hàm của mỗi hàm số sau: a) f(x) = 3x² – 2x + $\frac{2}{\mathrm{x}}$ ....

• Bài 29 trang 53 SBT Toán 12 Tập 2: Tính: a) $\underset{0}{\overset{\frac{\mathrm{\pi }}{4}}{\int }}{\sin }^2\frac{\mathrm{x}}{2}\mathrm{d}\mathrm{x}$;b) $\underset{0}{\overset{1}{\int }}\left(3\mathrm{x}-4{\mathrm{x}}^3\right)\mathrm{d}\mathrm{x}-\underset{1}{\overset{2}{\int }}\left(4{\mathrm{x}}^3-3\mathrm{x}\right)\mathrm{d}\mathrm{x}$; ....

• Bài 30 trang 53 SBT Toán 12 Tập 2: Cho hàm số f(x) có f'(x) = 10x – e^x với mọi x ∈ ℝ. Biết f(0) = 1, tính giá trị f(2) ....

• Bài 31 trang 53 SBT Toán 12 Tập 2: Một ô tô đang chạy với vận tốc 15 m/s thì tăng tốc, chuyển động nhanh dần đều ....

• Bài 32 trang 53 SBT Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi các đường y = $\sqrt{\mathrm{x}}$ − 2 ....

• Bài 33 trang 53 SBT Toán 12 Tập 2: Tính thể tích khối tròn xoay tạo thành khi quay quanh Ox hình phẳng giới hạn bởi ....

• Bài 34 trang 53 SBT Toán 12 Tập 2: Cho tứ diện đều ABCD có cạnh bằng a. Tính $\left(\overrightarrow{\mathrm{A}\mathrm{B}}+\overrightarrow{\mathrm{A}\mathrm{D}}\right).\overrightarrow{\mathrm{B}\mathrm{C}}$ ....

• Bài 35 trang 53 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho đường thẳng ∆: $\frac{\mathrm{x}-2}{1}=\frac{\mathrm{y}+2}{2}=\frac{\mathrm{z}-3}{2}$ ....

• Bài 36 trang 54 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho mặt cầu (S): x² + y² + (z – 2)² = 9 và mặt phẳng (P): 2x + 2y – z + 8 = 0 ....

• Bài 37 trang 54 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho hai đường thẳng: ∆: $\left\{\begin{array}{l}\mathrm{x}=3\\ \mathrm{y}=1+\mathrm{t}\\ \mathrm{z}=-1+3\mathrm{t}\end{array}\right.$  và ∆': $\left\{\begin{array}{l}\mathrm{x}=1+\mathrm{s}\\ \mathrm{y}=-2+3\mathrm{s}\\ \mathrm{z}=-5\end{array}\right.$ ....

• Bài 38 trang 54 SBT Toán 12 Tập 2: Trong không gian Oxyz, cho hai điểm A(1; 2; 0) và B(3; 2; 2) ....

• Bài 39 trang 54 SBT Toán 12 Tập 2: Một quả bóng được chuyền theo một đường parabol nằm trong một mặt phẳng (α) ....

• Bài 40 trang 54 SBT Toán 12 Tập 2: Đối với một vị trí P trong không trung, gọi M là giao điểm của tia OP với bề mặt Trái Đất ....

• Bài 41 trang 55 SBT Toán 12 Tập 2: Một nhóm học sinh áp dụng hai thiết bị để đo công suất của một chiếc quạt điện ....

• Bài 42 trang 55 SBT Toán 12 Tập 2: Nghiên cứu hiệu quả của hai loại thuốc hạ huyết áp A và B trên 4000 người ta thu được bảng ....

• Bài 43 trang 55 SBT Toán 12 Tập 2: Gieo ba con xúc xắc cân đối và đồng chất. Xét các biến cố sau: ....

• Bài 44 trang 55 SBT Toán 12 Tập 2: Một cặp trẻ sinh đôi có thể do cùng một trứng sinh ra (gọi đó là cặp song sinh cùng trứng) ....

• Bài 45 trang 55 SBT Toán 12 Tập 2: Thống kê cho thấy tỉ lệ người mắc bệnh X trong dân cư là 20% ....