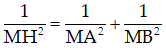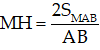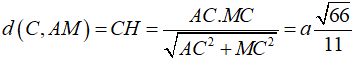20 dạng bài Vectơ trong không gian, Quan hệ vuông góc trong không gian chọn lọc - Toán lớp 11
20 dạng bài Vectơ trong không gian, Quan hệ vuông góc trong không gian chọn lọc
Với 20 dạng bài Vectơ trong không gian, Quan hệ vuông góc trong không gian chọn lọc Toán lớp 11 tổng hợp các dạng bài tập, 200 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Vectơ trong không gian, Quan hệ vuông góc trong không gian từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Tổng hợp lý thuyết chương Vectơ trong không gian. Quan hệ vuông góc trong không gian
- Lý thuyết Vectơ trong không gian
- Lý thuyết Hai đường thẳng vuông góc
- Lý thuyết Đường thẳng vuông góc với mặt phẳng
- Lý thuyết Hai mặt phẳng vuông góc
- Lý thuyết Khoảng cách
- Lý thuyết Tổng hợp chương Vectơ trong không gian. Quan hệ vuông góc trong không gian
Các dạng bài tập
- Các phép toán vectơ trong không gian Xem chi tiết
- Phân tích một vectơ theo các vectơ khác | Biểu diễn 1 vectơ theo 2, 3 vectơ không cùng phương Xem chi tiết
- Điều kiện để 2 vectơ cùng phương Xem chi tiết
- Điều kiện để 3 vectơ đồng phẳng Xem chi tiết
- Bài tập chứng minh đẳng thức vectơ Xem chi tiết
- Tìm tập hợp điểm thỏa mãn đẳng thức vectơ Xem chi tiết
Chủ đề: Hai đường thẳng vuông góc
- Câu hỏi trắc nghiệm lí thuyết hai đường thẳng vuông góc Xem chi tiết
- Xác định góc giữa hai vecto, góc giữa hai đường thẳng Xem chi tiết
- Tính tích vô hướng của hai vectơ Xem chi tiết
- Hai đường thẳng vuông góc trong không gian Xem chi tiết
Chủ đề: Đường thẳng vuông góc với mặt phẳng
- Câu hỏi trắc nghiệm lí thuyết đường thẳng vuông góc với mặt phẳng Xem chi tiết
- Chứng minh đường thẳng vuông góc với mặt phẳng Xem chi tiết
- Tính góc giữa đường thẳng và mặt phẳng Xem chi tiết
- Cách làm bài tập về tìm thiết diện Xem chi tiết
Chủ đề: Hai mặt phẳng vuông góc
- Câu hỏi trắc nghiệm lí thuyết hai mặt phẳng vuông góc Xem chi tiết
- Tính góc giữa hai mặt phẳng trong không gian Xem chi tiết
- Chứng minh hai mặt phẳng vuông góc trong không gian Xem chi tiết
- Tính độ dài đoạn thẳng trong không gian Xem chi tiết
- Xác định thiết diện chứa một đường thẳng và vuông góc với một mặt phẳng Xem chi tiết
Chủ đề: Khoảng cách
- Tính khoảng cách từ một điểm đến một đường thẳng Xem chi tiết
- Khoảng cách từ một điểm đến một mặt phẳng (sử dụng hình chiếu) Xem chi tiết
- Khoảng cách từ một điểm đến một mặt phẳng (dùng quan hệ song song) Xem chi tiết
- Khoảng cách giữa đường thẳng và mặt phẳng song song Xem chi tiết
- Khoảng cách giữa hai mặt phẳng song song Xem chi tiết
- Đoạn vuông góc chung của hai đường thẳng chéo nhau Xem chi tiết
- Đoạn vuông góc chung của hai đường thẳng chéo nhau trong không gian (dùng quan hệ song song) Xem chi tiết
Cách tìm điều kiện để 3 vectơ đồng phẳng
A. Phương pháp giải
* Để chứng minh ba vectơ đồng phẳng, ta có thể chứng minh bằng một trong các cách:
- Chứng minh các giá của ba vectơ cùng song song với một mặt phẳng.
- Dựa vào điều kiện để ba vectơ đồng phẳng: Nếu có m, n ∈ R: c→ = ma→ + nb→ thì a→ ; b→ ; c→ đồng phẳng.
+ Để phân tích một vectơ x ⃗ theo ba vectơ a→; b→; c→ không đồng phẳng, ta tìm các số m, n, p sao cho: x→ = ma→ + nb→ + pc→ .
B. Ví dụ minh họa
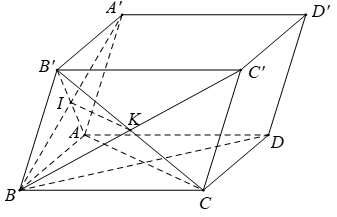
Ví dụ 1: Cho hình hộp ABCD.A’B’C’D’. Gọi I và K lần lượt là tâm của hình bình hành ABB’A’ và BCC’B’. Khẳng định nào sau đây sai?
A. IK→ = (1/2)AC→ = (1/2)A'C'→
B. Bốn điểm I; K; C; A đồng phẳng.
C. BD→ + 2IK→ = 2BC→
D. Ba vectơ BD→ ; IK→ ; B'C'→ không đồng phẳng.
Hướng dẫn giải
Chọn D.
Ta xét các phương án:
+ A đúng do tính chất đường trung bình trong tam giác A’BC’ và tính chất của hình bình hành ACC’A’.
+ B đúng do IK là đường trung bình của tam giác AB’C nên IK // AC
⇒ bốn điểm I; K; C; A đồng phẳng.
+ C đúng do việc ta phân tích:
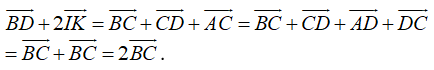
+ D sai do giá của ba vectơ BD→ ; IK→ ; B'C'→ đều song song hoặc trùng với mặt phẳng . Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
Ví dụ 2: Cho ba vectơ a→ ; b→ ; c→ không đồng phẳng. Xét các vectơ x→ = 2a→ + b→, y→ = a→ - b→ - c→, z→ = -3b→ - 2c→. Chọn khẳng định đúng?
A. Ba vectơ x→, y→, z→ đồng phẳng
B. Ba vectơ x→, a→ cùng phương
C. Ba vectơ x→, b→ cùng phương
D. Ba vectơ x→, y→, z→ đôi một cùng phương
Hướng dẫn giải
Chọn A.
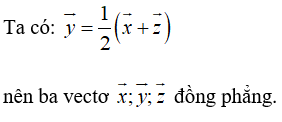
Ví dụ 3: Cho hình hộp ABCD.EFGH. Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành BCGF. Trong các khẳng định sau, khẳng định nào đúng?
A. BD→, AK→, GF→ đồng phẳng
B. BD→, IK→, GF→ đồng phẳng
C. BD→, EK→, GF→ đồng phẳng
D. BD→, IK→, GC→ đồng phẳng
Hướng dẫn giải
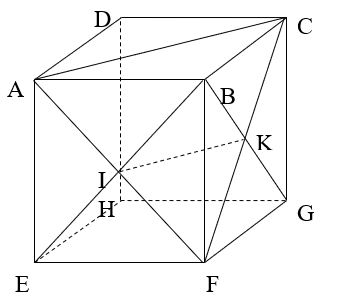
Chọn B.
+ Xét tam giác FAC có I; K lần lượt là trung điểm của AF và FC nên IK là đường trung bình của tam giác.
⇒ IK // AC nên IK // mp (ABCD) .
+ BC // GF nên GF // mp(ABCD)
+ 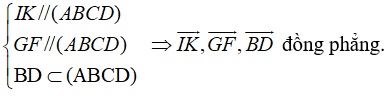
Ví dụ 4: Trong các khẳng định sau, khẳng định nào sai?
A. Nếu giá của ba vectơ a→; b→; c→ cắt nhau từng đôi một thì ba vectơ đó đồng phẳng.
B. Nếu trong ba vectơ a→; b→; c→ có một vectơ 0→ thì ba vectơ đó đồng phẳng.
C. Nếu giá của ba vectơ a→; b→; c→ cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.
D. Nếu trong ba vectơ a→; b→; c→ có hai vectơ cùng phương thì ba vectơ đó đồng phẳng.
Hướng dẫn giải
Chọn A.
Ví dụ hình lập phương ABCD.A’B’C’D’ có giá ba vecto AB→; AD→ và AA'→ đôi một cắt nhau nhưng ba vecto đó không đồng phẳng.
Cách xác định góc giữa hai vecto, góc giữa hai đường thẳng
A. Phương pháp giải
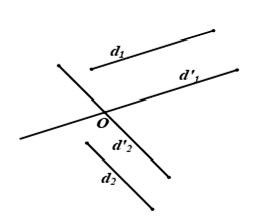
Để tính góc giữa hai đường thẳng d1; d2 trong không gian ta có thể thực hiện theo hai cách
Cách 1. Tìm góc giữa hai đường thẳng d1, d2 bằng cách chọn một điểm O thích hợp (O thường nằm trên một trong hai đường thẳng).
Lưu ý 1: Để tính góc này ta thường sử dụng định lí côsin trong tam giác
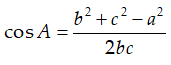
Cách 2. Tìm hai vec tơ chỉ phương u1, u2 của hai đường thẳng d1, d2
Khi đó góc giữa hai đường thẳng d1, d2 xác định bởi cos(d1, d2) = 
Lưu ý 2: Để tính u1→, u2→, |u1→|, |u2→| ta chọn ba vec tơ a→, b→, c→ không đồng phẳng mà có thể tính được độ dài và góc giữa chúng,sau đó biểu thị các vec tơ u1→, u2→ qua các vec tơ a→, b→, c→ rồi thực hiện các tính toán.
B. Ví dụ minh họa
Ví dụ 1: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB→ và DH→
A. 45° B. 90° C. 120° D.60°
Hướng dẫn giải:
Vì DH→ = AE→ ( ADHE là hình vuông) nên (AB→, DH→) = (AB→, AE→) = ∠BAE = 90° (ABFE là hình vuông).
Chọn B
Ví dụ 2: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB→ và EG→?
A. 90° B. 60° C. 45° D. 120°
Hướng dẫn giải
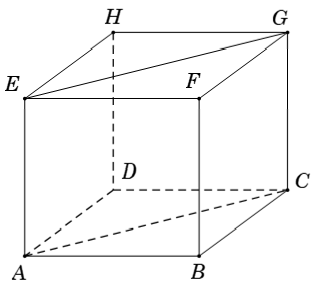
Vì EG→ = AC→ ( tứ giác AEGC là hình chữ nhật) nên:
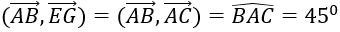
Chọn C.
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa AC và DA’ là:
A. 45° B. 90° C. 60° D. 120°
Hướng dẫn giải
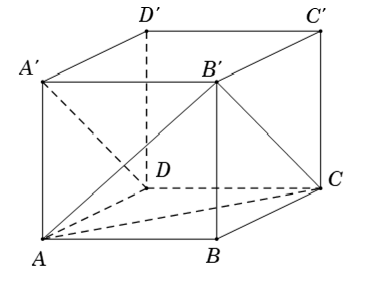
Gọi a là độ dài cạnh hình lập phương
Khi đó, tam giác AB’C đều (AB' = B'C = CA = a√2) do đó ∠B'CA= 60° .
Lại có, DA’ song song CB’ nên
(AC, DA') = (AC, CB') = ∠ACB'= 60°.
Chọn C
Cách tính khoảng cách từ một điểm đến một đường thẳng
A. Phương pháp giải
- Để tính khoảng cách từ điểm M đến đường thẳng Δ ta cần xác định được hình chiếu H của điểm M trên đường thẳng Δ. Khi đó MH chính là khoảng cách từ M đến đường thẳng. Điểm H thường được dựng theo hai cách sau:
+ Trong mp(M; Δ) vẽ MH vuông góc Δ ⇒ d(M; Δ) = MH
+ Dựng mặt phẳng (α) qua M và vuông góc với Δ tại H ⇒ d(M; Δ) = MH.
- Hai công thức sau thường được dùng để tính MH:
+ Tam giác AMB vuông tại M và có đường cao AH thì
+ MH là đường cao của tam giác MAB thì
B. Ví dụ minh họa
Ví dụ 1: Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2; BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?
A. 2a B. 4a C.3a D. 5a
Hướng dẫn giải
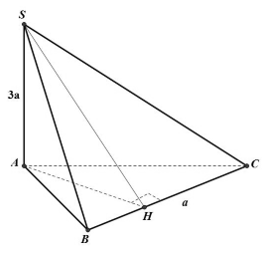
+ Kẻ AH vuông góc với BC
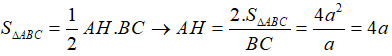
Ta có: SA ⊥ (ABC) ⇒ SA ⊥ BC
Lại có: AH ⊥ BC nên BC ⊥ (SAH)
⇒ SH ⊥ BC và khoảng cách từ S đến BC chính là SH
+ Ta có tam giác vuông SAH vuông tại A nên ta có
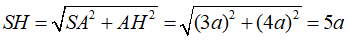
Chọn D
Ví dụ 2: Cho hình chóp ABCD có cạnh AC ⊥ (BCD) và BCD là tam giác đều cạnh bằng a. Biết AC = a√2 và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
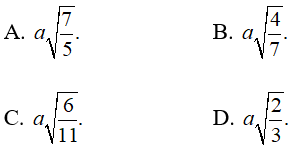
Hướng dẫn giải
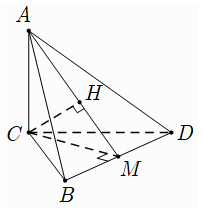
+ Do tam giác BCD đều cạnh a nên đường trung tuyến CM đồng thời là đường cao và MC = a√3/2
+ Ta có: AC ⊥ (BCD) ⇒ AC ⊥ CM
Gọi H là chân đường vuông góc kẻ từ C đến AM
Ta có:
Chọn đáp án C
Ví dụ 3: Cho tứ diện SABC trong đó SA; SB; SC vuông góc với nhau từng đôi một và SA = 3a; SB = a; SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:

Hướng dẫn giải
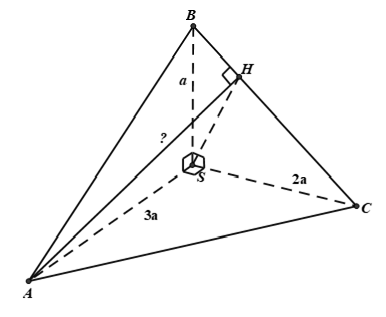
Chọn đáp án B
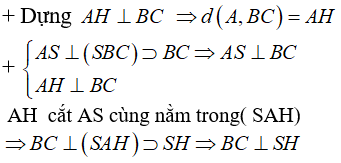
Xét trong tam giác SBC vuông tại S có SH là đường cao ta có:
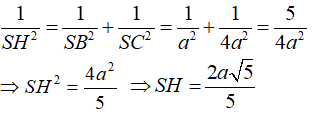
+ Ta dễ chứng minh được AB ⊥ (SBC) ⊃ SH ⇒ AS ⊥ SH
⇒ tam giác SAH vuông tại S.
Áp dụng định lsi Pytago trong tam giác ASH vuông tại S ta có:
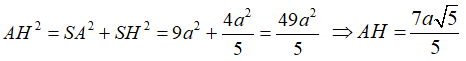
Chọn B