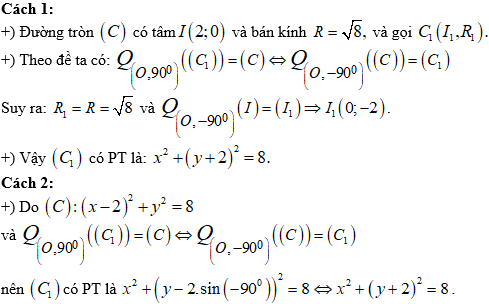10 dạng bài tập Phép dời hình và phép đồng dạng trong mặt phẳng chọn lọc - Toán lớp 11
10 dạng bài tập Phép dời hình và phép đồng dạng trong mặt phẳng chọn lọc
Với 10 dạng bài tập Phép dời hình và phép đồng dạng trong mặt phẳng chọn lọc Toán lớp 11 tổng hợp các dạng bài tập, 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phép dời hình và phép đồng dạng trong mặt phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 11.
Tổng hợp lý thuyết chương Phép dời hình và phép đồng dạng trong mặt phẳng
- Lý thuyết Phép biến hình
- Lý thuyết Phép tịnh tiến
- Lý thuyết Phép đối xứng trục
- Lý thuyết Phép đối xứng tâm
- Lý thuyết Phép quay
- Lý thuyết Khái niệm về phép dời hình và hai hình bằng nhau
- Lý thuyết Phép vị tự
- Lý thuyết Phép đồng dạng
- Lý thuyết Tổng hợp chương Phép dời hình và phép đồng dạng trong mặt phẳng
Các dạng bài tập
- Các bài toán về phép tịnh tiến
- Các bài toán về phép đối xứng tâm
- Các bài toán về phép đối xứng trục
- Các bài toán về phép quay
- Các bài toán về phép vị tự
- Các bài toán về phép đồng dạng
Các dạng bài tập chương Phép dời hình và phép đồng dạng trong mặt phẳng
Chủ đề: Phép tịnh tiến
- Tính chất của phép tịnh tiến cực hay Xem chi tiết
- Cách tìm ảnh của 1 điểm qua phép tịnh tiến cực hay Xem chi tiết
- Cách tìm ảnh của 1 đường thẳng qua phép tịnh tiến cực hay Xem chi tiết
- Cách tìm ảnh của 1 đường tròn qua phép tịnh tiến cực hay Xem chi tiết
Chủ đề: Phép đối xứng trục
- Tính chất đối xứng trục cực hay Xem chi tiết
- Tìm ảnh của một điểm qua phép đối xứng trục cực hay Xem chi tiết
- Tìm ảnh của một đường thẳng qua phép đối xứng trục cực hay Xem chi tiết
- Tìm ảnh của một đường tròn qua phép đối xứng trục cực hay Xem chi tiết
Chủ đề: Phép đối xứng tâm
- Tìm ảnh của một điểm qua phép đối xứng tâm cực hay Xem chi tiết
- Tìm ảnh của một đường thẳng qua phép đối xứng tâm cực hay Xem chi tiết
- Tìm ảnh của một đường tròn qua phép đối xứng tâm cực hay Xem chi tiết
- Cách tìm tâm đối xứng cực hay Xem chi tiết
Chủ đề: Phép quay
- Dạng bài tập về phép quay 90 độ cực hay Xem chi tiết
- Dạng bài tập về phép quay 180 độ cực hay Xem chi tiết
- Cách tìm ảnh của điểm qua phép quay cực hay Xem chi tiết
- Cách tìm ảnh của đường thẳng qua phép quay cực hay Xem chi tiết
- Cách tìm ảnh của đường tròn qua phép quay cực hay Xem chi tiết
Chủ đề: Vị tự
- Tìm ảnh của một điểm qua phép vị tự cực hay Xem chi tiết
- Tìm ảnh của một đường thẳng qua phép vị tự cực hay Xem chi tiết
- Tìm ảnh của một đường tròn qua phép vị tự cực hay Xem chi tiết
Cách tìm ảnh của 1 đường thẳng qua phép tịnh tiến
A. Phương pháp giải
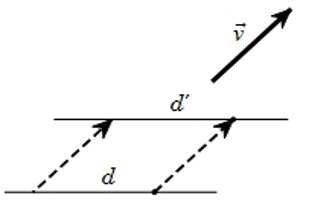
+) Sử dụng tính chất: d' là ảnh của d qua phép 
thì d' song song hoặc trùng với d
Nếu: d: Ax + By + C = 0; d'//d ⇒ d': Ax + By + C' = 0 (C' ≠ C)
+) Sử dụng biểu thức tọa độ
+) Chú ý: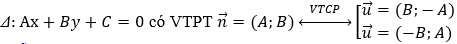 
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho 
= (1;-3) và đường thẳng d có phương trình 2x - 3y + 5 = 0. Viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến .
Hướng dẫn giải:
Cách 1. Sử dụng biểu thức tọa độ của phép tịnh tiến.
Lấy điểm M(x;y) tùy ý thuộc d, ta có 2x - 3y + 5 = 0 (*)
Cách 2. Sử dụng tính chất của phép tịnh tiến
Do d' = (d) nên d' song song hoặc trùng với d, vì vậy phương trình đường thẳng d' có dạng 2x - 3y + c = 0.(**)
Lấy điểm M(-1;1) ∈ d. Khi đó M' = (M) = (-1 + 1;1 - 3) = (0;-2).
Do M' ∈ d' ⇒ 2.0 - 3.(-2) + c = 0 ⇔ c = -6
Vậy ảnh của d là đường thẳng d': 2x - 3y - 6 = 0.
Cách 3. Để viết phương trình d' ta lấy hai điểm phân biệt M,N thuộc d, tìm tọa độ các ảnh M', N' tương ứng của chúng qua . Khi đó d' đi qua hai điểm M' và N'.
Cụ thể: Lấy M(-1;1), N(2;3) thuộc d, khi đó tọa độ các ảnh tương ứng là M'(0;-2), N'(3;0). Do d' đi qua hai điểm M', N' nên có phương trình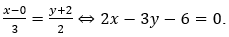 
Ví dụ 2: Tìm PT đt d qua phép tịnh tiến theo : d biến thành d’, biết: d’: 2x + 3y – 1 = 0 với = (-2;-1)
Hướng dẫn giải:
* Cách 1: Gọi (d) = d'. Khi đó d // d’ nên PT đt d có dạng: 2x + 3y + C = 0
Chọn A’(2;-1) ∈ d’. Khi đó: (A) = A' ⇒ A(4; 0) ∈ d nên 8 + 0 + C = 0 ⇔ C = -8
Vậy: d: 2x + 3y – 8 = 0
* Cách 2: Chọn A’(2; -1) ∈ d’, (A) = A' ⇒ A(4; 0) ∈ d và chọn B’(-1;1) ∈ d’, (B) = B' ⇒ B(1;2) ∈ d
Đt d đi qua 2 điểm A, B nên PT đt d là:
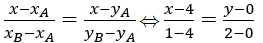
⇔ 2x – 8 = -3y
⇔ 2x + 3y – 8 = 0
* Cách 3: Gọi M’(x’;y’) ∈ d’, (M) = M'
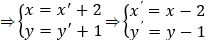
Ta có: M’ ∈ d’
⇔ 2x’ + 3y’ – 1 = 0
⇔ 2x – 4 + 3y – 3 – 1 = 0
⇔ 2x + 3y – 8 = 0
⇔ M ∈ d: 2x + 3y – 8 = 0
Ví dụ 3: Tìm tọa độ vectơ sao cho (d) = d' với d: 3x – y + 1 = 0 và d’: 3x – y – 7 = 0
Hướng dẫn giải:
d' là ảnh của d qua phép thì d' song song hoặc trùng với d
Nhận thấy d//d’ nên với mỗi điểm A ∈ d; B ∈ d' ta có:
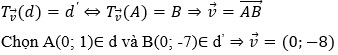
Ví dụ 4: Phép tịnh tiến theo vectơ = (3;m). Tìm m để đt d: 4x + 6y – 1 = 0 biến thành chính nó qua phép tịnh tiến theo vectơ
Hướng dẫn giải:
Tìm ảnh của một đường thẳng qua phép đối xứng trục
A. Phương pháp giải
Cách 1. Sử dụng tính chất của phép đối xứng trục
Cách 2. Sử dụng biểu thức tọa độ đối với phép đối xứng qua trục Ox hoặc Oy
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x + y - 3 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng trục Ox.
Hướng dẫn giải:
Trục Ox có phương trình y = 0.
• Tọa độ giao điểm A của d và Ox là nghiệm của hệ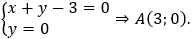 
• Vì A ∈ Ox nên qua phép đối xứng trục Ox biến thành chính nó, tức A'≡A(3;0).
Chọn điểm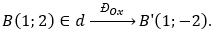 
• Gọi đường thẳng d' là ảnh của d qua phép đối xứng trục Ox khi đó d’ đi qua hai điểm A'(3;0) và B'(1;-2)
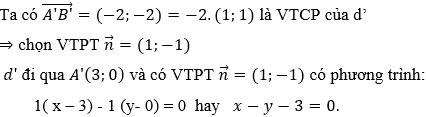
Ví dụ 2: Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ có phương trình 7x + y - 3 = 0. Tìm ảnh của Δ qua phép đối xứng trục Oy.
Hướng dẫn giải:
(Sử dụng biểu thức tọa độ)
Biểu thức tọa độ qua phép đối xứng trục tung là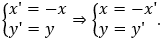 
Thay vào Δ, ta được 7(-x') + y' - 3 = 0 hay 7x' - y' + 3 = 0.
Vậy ảnh của Δlà: Δ': 7x - y + 3 = 0
Ví dụ 3: Cho đường thẳng (d) có phương trình x + y-7 = 0 và đường thẳng (Δ) có phương trình 2x - y - 2 = 0. Phương trình đường thẳng (d') là ảnh của đường thẳng (d) qua phép đối xứng trục (Δ) là
Hướng dẫn giải:
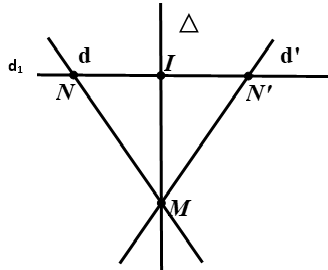
• Gọi M = (d)∩(Δ) khi đó tọa độ của M là nghiệm của hệ: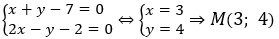 
Lấy N(1;6) ∈ (d).
• Gọi (d1) là đường thẳng qua N và vuông góc với (Δ), khi đó: (d1): x + 2y + c = 0
N(1;6) ∈ (d1) ⇒ 1 + 2.6 + c = 0 ⇒ c = -13 ⇒ (d1): x + 2y - 13 = 0
• Gọi I = (d1)∩(Δ) khi đó tọa độ của I là nghiệm của hệ: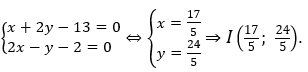 
• Gọi N' là ảnh của N qua phép đối xứng trục (Δ) ⇒ I là trung điểm của NN' nên suy ra: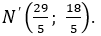 
• (d') là ảnh của đường thẳng (d) qua phép đối xứng trục (Δ)
Tìm ảnh của một đường thẳng qua phép đối xứng tâm
A. Phương pháp giải
[Cách 1]. Sử dụng tính chất:
Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
[Cách 2]. Sử dụng biểu thức tọa độ (phương pháp quỹ tích)
Trong hệ tọa độ Oxy
● Nếu tâm đối xứng là O(0;0), với mỗi M(x;y) gọi M' = DO(M) = (x';y') thì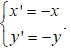 
● Nếu tâm đối xứng I(a;b) bất kì, với mỗi M(x;y) gọi M' = DI(M) = (x';y') thì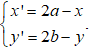 
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng Oxy cho đường thẳng d có phương trình: x + y + 2 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng tâm I(1;0)
Hướng dẫn giải:
d:x + y + 2 = 0 lấy 2 điểm A(0,-2), B(-2,0) thuộc d.
Gọi A’, B’ là ảnh của A,B qua phép đối xứng tâm I. Khi đó ta có:
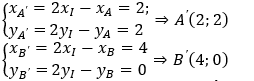
Gọi d’ là ảnh của d qua phép đối xứng tâm I. Khi đó d’ đi qua 2 điểm A’B’ nên có phương trình d': x + y- 4 = 0
Vậy ảnh của d là d': x + y- 4 = 0
Ví dụ 2: Trong mặt phẳng Oxy cho đường thẳng d có phương trình: 2x + y + 1 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng tâm I(1;0)
Hướng dẫn giải:
• d: 2x + y + 1 = 0 lấy 2 điểm A(0,-1), B (-1,1) thuộc d. Gọi A’, B’ là ảnh của A, B qua phép đối xứng tâm I. Khi đó ta có:
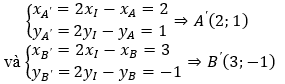
• Gọi d’ là ảnh của d qua phép đối đối xứng tâm I. Khi đó, d’ đi qua 2 điểm A’ và B’ nên có phương trình d’: đi qua A’( 2;1),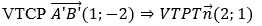 
Phương trình d’: 2(x - 2) + 1(y - 1) = 0 hay 2x + y - 5 = 0
Vậy ảnh của d là d': 2x + y - 5 = 0
Ví dụ 3: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 6y + 5 = 0, điểm I(2;-4). Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng tâm I
Hướng dẫn giải:
Lấy M(x;y) thuộc d, phép đối xứng tâm I(x0,y0) biến M(x;y) thành M'(x',y') thì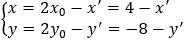 
. Thay vào phương trình d ta được
2(4 - x') - 6(-8 - y') + 5 = 0 ⇔ 2x' - 6y' - 61 = 0 hay 2x - 6y - 61 = 0.
Dạng bài tập về phép quay 90 độ
A. Phương pháp giải
[1]. Biểu thức tọa độ của phép quay 90° và -90°
Trong hệ trục tọa Oxy:
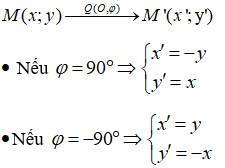
[2]. Bài toán xác định vị trí của điểm, hình khi thực hiện phép quay cho trước
Bước 1. Xác định tâm quay và góc quay theo yêu cầu bài toán.
Bước 2. Áp dụng các kiến thức sau:
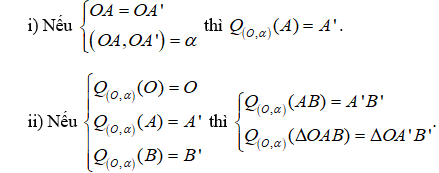
Bước 3. Kết luận.
B. Ví dụ minh họa
Ví dụ 1: Cho tam giác ABC, trọng tâm G ( thứ tự các điểm như hình vẽ)
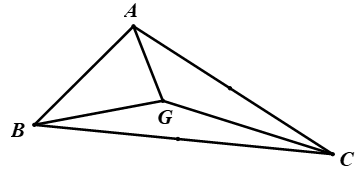
a) Tìm ảnh của điểm B qua phép quay tâm A góc quay 90°
b) Tìm ảnh của đường thẳng BC qua phép quay tâm A góc quay 90°
c) Tìm ảnh của tam giác ABC qua phép quay tâm G góc quay 90°
Hướng dẫn giải:
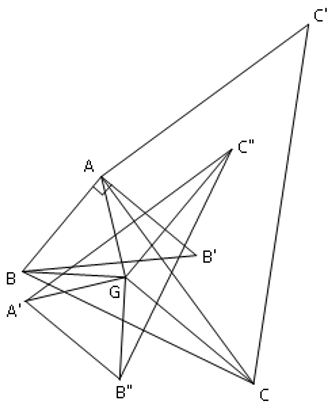
a)
Dựng đoạn thẳng AB’ bằng đoạn thẳng AB sao cho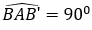 
(Vị trí B’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)
• Khi đó: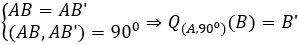 
• Vậy B’ à ảnh của điểm B qua phép quay tâm A, góc quay 90°
b)
• Dựng đoạn thẳng AC’ bằng đoạn thẳng AC sao cho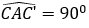 
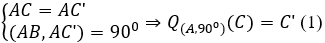
(Vị trí C’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)
• 
Mặt khác, Q(A,90°)(B) = B' (theo câu a) (2)
• Từ (1) và (2) suy ra: Q(A,90°)(BC) = B'C'
c)
• Dựng đoạn thẳng GA’ bằng đoạn thẳng GA sao cho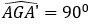 
(Vị trí A’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)
• Dựng đoạn thẳng GB’’ bằng đoạn thẳng GB sao cho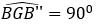 
(Vị trí B’’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)
• Dựng đoạn thẳng GC’’ bằng đoạn thẳng GC sao cho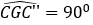 
(Vị trí C’’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)
• Khi đó:
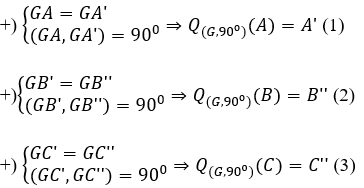
Từ (1),(2),(3) suy ra: Q(G,90°)(ΔABB) = ΔAB''C''
Ví dụ 2: Cho hình vuông ABCD tâm O ( thứ tự các điểm như hình vẽ)
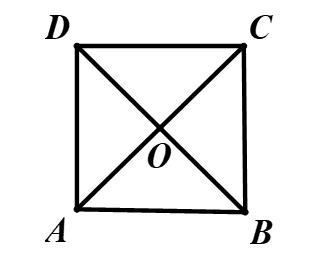
a) Tìm ảnh của điểm C qua phép quay tâm A, góc quay 90°
b) Tìm ảnh của đường thẳng BC qua phép quay tâm O, góc quay 90°
Hướng dẫn giải:
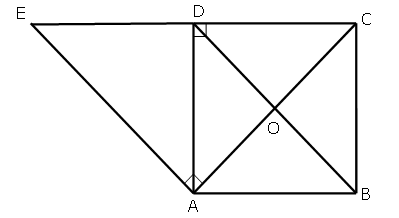
a) Gọi E là điểm đối xứng của C qua D.
Khi đó: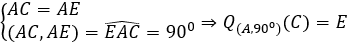 
Vậy E là ảnh của C qua phéo quay tâm A, góc quay 90°
b) Vì ABCD là hình vuông nên
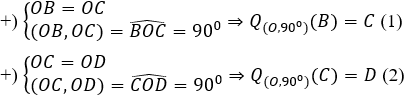
Từ (1) và (2) suy ra: Q(O,90°)(BC) = CD
Vậy CD là ảnh của BC qua phép quay tâm O góc quay 90°
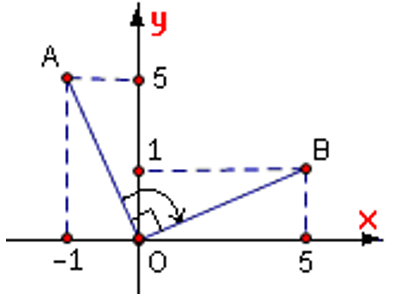
Ví dụ 3: Trong mặt phẳng tọa độ Oxy cho điểm A(-1;5); đường thẳng d: 3x - y + 2 = 0 và đường tròn (C): (x + 4)2 + (y - 1)2 = 16
a) Tìm tọa độ điểm B là ảnh của điểm A qua phép quay tâm O(0;0) góc quay -90°.
b) Viết phương trình đường thẳng d' là ảnh của d qua phép quay tâm O góc quay -90°.
c) Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay -90°
Hướng dẫn giải:
a)
Cách 1:
+) Do Q(O,90°)(A) = B nên dựa vào vẽ bên ta suy ra: B(5;1).
Cách 2:
+) Do Q(O,90°)(A) = B nên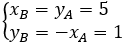 
.
Vậy B(5;1).
b) Qua phép quay tâm O góc quay -90° đường thẳng d biến thành đường thẳng d' vuông góc với d.
Phương trình đường thẳng d' có dạng: x + 3y + m = 0.
Lấy A(0;2) ∈ d. Qua phép quay tâm O góc quay -90°, điểm A(0;2) biến thành điểm B(2;0) ∈ d'. Khi đó m = -2.
Vậy phương trình đường d' là x + 3y - 2 = 0.
c) Từ (C), ta có tâm I(-4; 1) và bán kính R = 4.
Khi đó: Q(O,90°)(I) = I'(1;4) và bán kính R' = R = 4.
Vậy: Q(O,90°)(C) = (C'): (x - 1)2 + (y - 4)2 = 16
C. Bài tập trắc nghiệm
Câu 1. Cho hình vuông ABCD tâm O, M là trung điểm của AB, N là trung điểm của OA ( thứ tự các điểm A,B,C,D như hình vẽ)
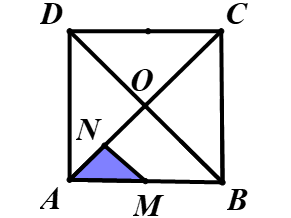
Tìm ảnh của ΔAMN qua phép quay tâm O, góc quay 90°.
A. ΔDM’N’, M’, N’ lần lượt là là trung điểm OC, OB
B. ΔDM’N’, M’, N’ lần lượt là là trung điểm OA, OB
C. ΔAM’N’, M’, N’ lần lượt là là trung điểm OC, OD
D. ΔAM’N’ với M’, N’ lần lượt là là trung điểm BC, OB
Lời giải:
.
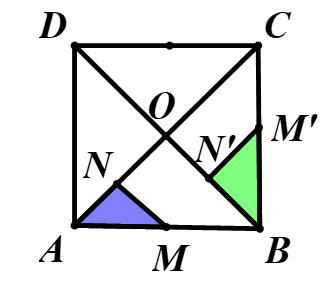
Chọn D.
Câu 2. Cho hai hình vuông vuông ABCD và BEFG (như hình vẽ). Tìm ảnh của ΔABG trong phép quay tâm B, góc quay -90°.
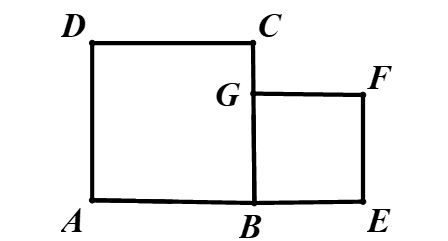
A. ΔCBE
B. ΔCBF
C. ΔCBG
D. ΔCBD
Lời giải:
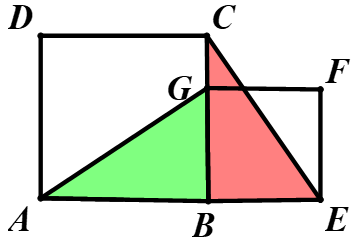
Chọn A.
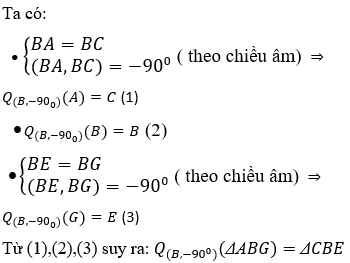
Câu 3. Cho hình vuông ABCD có tâm là O,. Gọi M,N,P,Q theo thứ tự là trung điểm các cạnh AD, DC, CB, BA ( xem hình vẽ)
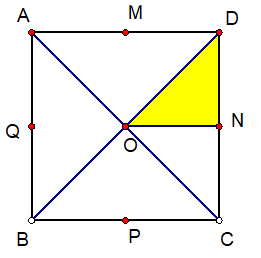
Tìm ảnh của tam giác ODN qua phép quay tâm O góc quay -90°.
A. ΔOCP
B. ΔOCM
C. ΔMCP
D. ΔNCP
Lời giải:
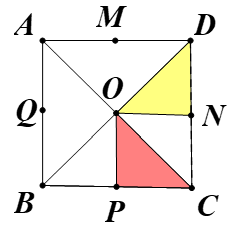
Chọn A
+) Ta có:
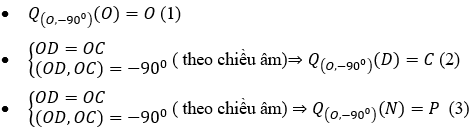
+) Từ (1), (2), (3) suy ra: Q(O,-90°)(ΔODN) = ΔOCP.
Câu 4. Trong mặt phẳng Oxy, ảnh của điểm M(-6;1) qua phép quay Q(O,90°)là:
A. M(1;6).
B. M(-1;-6).
C. M(-6;-1).
D. M(6;1).
Lời giải:
Chọn B
Cho điểm M(x;y). Khi đó Q(O,90°)(M) = M'(-y;x).
Do đó, với điểm M(-6;1) thì Q(O,90°)(M) = M'(-1;-6).
Câu 5. Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm M(2;0) và điểm N(0;2). Phép quay tâm O biến điểm M thành điển N, khi đó góc quay của nó là
A. φ = 30°.
B. φ = 45°.
C. φ = 90°.
D. φ = 270°.
Lời giải:
Chọn C
+ Q(O;φ): M(x;y) ↦ N(x';y'). Khi đó: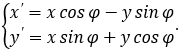 
Thử đáp án ta nhận φ = 90°.
+ Hoặc biểu diễn trên hệ trục tọa độ ta cũng được đáp án tương tự
Câu 6. Trong mặt phẳng Oxy, cho điểm B(-3;6). Tìm toạ độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay(-90°).
A. E(6;3).
B. E(-3;-6).
C. E(-6;-3).
D. E(3;6).
Lời giải:
Chọn C.
Điểm E(-6;-3).
Câu 7. Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng Δ: x + 2y - 6 = 0. Viết phương trình đường thẳng Δ' là ảnh của đường thẳng Δ qua phép quay tâm O góc 90°?
A. 2x - y + 6 = 0.
B. 2x - y-6 = 0.
C. 2x + y + 6 = 0.
D. 2x + y-6 = 0.
Lời giải:
Chọn A
Ta có Δ' ⊥ Δ ⇒ Δ': 2x - y+c = 0.
Lấy M(0;3) ∈ Δ, phép quay Q(O,90°) biến điểm M(0;3) thành điểm M'(-3;0).
Thế tọa độ điểm M'(-3;0) vào phương trình đường Δ': 2x - y + c = 0 ta được c = 6.
Vậy phương trình đường Δ': 2x - y + 6 = 0.
Câu 8. Trong mặt phẳng Oxy, cho đường tròn (C): (x - 2)2 + y2 = 8. Viết phương trình đường tròn (C1) sao cho (C) là ảnh của đường tròn (C1) qua phép quay tâm O, góc quay 90°.
A. x2 + (y + 2)2 = 8.
B. x2 + (y + 2)2 = 4.
A. (x - 2)2 + y2 = 8.
C. x2 + (y - 2)2 = 8.
Lời giải:
Chọn A
