20 dạng bài Dãy số, Cấp số cộng và cấp số nhân chọn lọc - Toán lớp 11

20 dạng bài Dãy số, Cấp số cộng và cấp số nhân chọn lọc

Với 20 dạng bài Dãy số, Cấp số cộng và cấp số nhân chọn lọc Toán lớp 11 tổng hợp các dạng bài tập, 200 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Dãy số, Cấp số cộng và cấp số nhân từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

20 dạng bài Dãy số, Cấp số cộng và cấp số nhân chọn lọc

Tổng hợp lý thuyết chương Dãy số - Cấp số cộng và cấp số nhân

Các dạng bài tập chương Dãy số - Cấp số cộng, cấp số nhân

Phương pháp quy nạp toán học

Dãy số

Cấp số cộng

Cấp số nhân

Cách tìm số hạng thứ n của dãy số

A. Phương pháp giải

Cho dãy số bởi công thức của số hạng tổng quát: u_n = f(n). Khi đó số hạng đứng thứ k của dãy số là: u_k = f(k).

B. Ví dụ minh họa

Ví dụ 1: Cho dãy số (u_n) với u_n = 2n+ 1. Mệnh đề nào sau đây là sai?

A. u₃ là số nguyên tố. B. u₅ không chia hết cho 5

C. u₇ = 15 D. u₈ = 18

Hướng dẫn giải:

Ta xét các phương án:

+ Ta có: u₃ = 2 . 3 + 1 = 7 là số nguyên tố

=> A đúng

+ u₅ = 2 . 5 + 1 = 11 là số không chia hết cho 5.

=> B đúng

+ u₇ = 2 . 7 + 1 = 15 nên C đúng .

+ u₈ = 2 . 8 + 1 = 17 nên D sai

Chọn D.

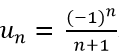
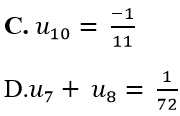
Ví dụ 2: Cho dãy số (u_n) với Cách tìm số hạng thứ n của dãy số cực hay có lời giải .Khẳng định nào sau đây là đúng?

Hướng dẫn giải:

Ta xét các phương án:

+ Ba số hạng đầu tiên của dãy số là: 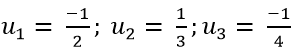Cách tìm số hạng thứ n của dãy số cực hay có lời giải => A sai.

+ Tổng hai số hạng đầu tiến là: 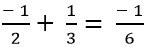Cách tìm số hạng thứ n của dãy số cực hay có lời giải => B đúng

+ Số hạng thứ 10 là 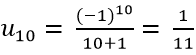Cách tìm số hạng thứ n của dãy số cực hay có lời giải => C sai.

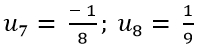
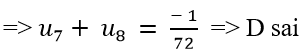
+ ta có: Cách tìm số hạng thứ n của dãy số cực hay có lời giải

Chọn B.

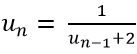
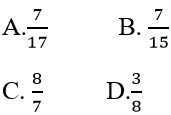
Ví dụ 3: Cho dãy số (un ) được xác định bởi u₁ = 1 và Cách tìm số hạng thứ n của dãy số cực hay có lời giải với mọi n ≥ 2. Tìm số hạng thứ 4 của dãy số.

Hướng dẫn giải:

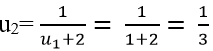
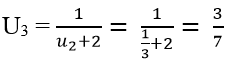
Ta có: Cách tìm số hạng thứ n của dãy số cực hay có lời giải

Và 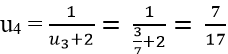Cách tìm số hạng thứ n của dãy số cực hay có lời giải

Chọn A.

Cách chứng minh một dãy số là cấp số cộng

A. Phương pháp giải

* Để chứng minh dãy số (u_n) là một cấp số cộng, ta xét A = u_n+1 − u_n

Nếu A là hằng số thì (u_n) là một cấp số cộng với công sai d = A.

Nếu A phụ thuộc vào n thì (u_n) không là cấp số cộng.

* Ngoài ra; để chứng minh dãy số (u_n) không là cấp số cộng ta có thể chỉ ra: tồn tại số nguyên dương k sao cho: u_k+1 − u_k ≠ u_k − u_k−1

B. Ví dụ minh họa

Ví dụ 1: Chứng minh dãy số (u_n) với u_n = 17n + 2 là cấp số cộng

Hướng dẫn giải:

Ta có: u_n+1 = 17(n + 1) + 2 = 17n + 19

=> Hiệu: u_n+1 – u_n = (17n + 19) − (17n + 2) = 17

Suy ra: (u_n) là cấp số cộng với công sai d = 17.

Ví dụ 2: Chứng minh dãy số (u_n) với u_n = 10 − 5n là cấp số cộng.

Hướng dẫn giải:

Ta có: u_n+1 = 10 − 5(n+1)= 5 − 5n.

Xét hiệu: u_n+1 − u_n = (5 − 5n) − (10 − 5n) = −5

=> (u_n) là một cấp số cộng với công sai d = −5.

Ví dụ 3: Cho dãy số (u_n) với u_n = 2n + 3. Chứng minh rằng dãy số (u_n) không phải là cấp số cộng .

Hướng dẫn giải:

Ta có: u_n+1 = 2ⁿ⁺¹ + 3

Xét hiệu: u_n+1 − u_n = (2ⁿ⁺¹ + 3) − (2ⁿ + 1)= 2ⁿ⁺¹ − 2ⁿ

=> (u_n+1 − u_n) không phải là hằng số; còn phụ thuộc vào n. Nên dãy số (u_n) không là cấp số cộng.

Điều kiện để dãy số là cấp số cộng, cấp số nhân

A. Phương pháp giải & Ví dụ

Ba số hạng u_k, u_k+1, u_k+2 là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi

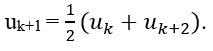
Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án

Ba số hạng u_k, u_k+1, u_k+2 là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi

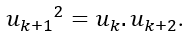
Ví dụ minh họa

Bài 1: Cho hai số -3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành cấp số cộng có công sai d = 2 Tìm n.

Lời giải:

Khi xen vào giữa hai số -3 và 23 n số hạng thì ta được một CSC với công sai d = 2. Nên suy ra CSC trên có n + 2 số hạng và 23 là số hạng thứ n + 2.

Khi đó ta có: 23 = -3 + (n + 1)2 ⇒ n = 12.

Bài 2: Cho các số -4, 1, 6, x theo thứ tự lập thành một cấp số cộng. Tìm x?

Lời giải:

Vì dãy số -4, 1, 6, x theo thứ tự lập thành một CSC nên ta có: (x+1)/2=6 ⇔ x=11.

Bài 3: Với giá trị x nào dưới đấy thì các số -4, x, -9 theo thứ tự đó lập thành một cấp số nhân?

Lời giải:

Vì dãy số -4, x, -9 theo thứ tự đó lập thành một cấp số nhân nên ta có:

x²=36 ⇔ x = ±6.

Xem thêm các dạng bài tập Toán lớp 11 chọn lọc, có đáp án hay khác:

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 11

20 dạng bài Dãy số, Cấp số cộng và cấp số nhân chọn lọc - Toán lớp 11