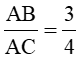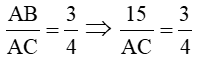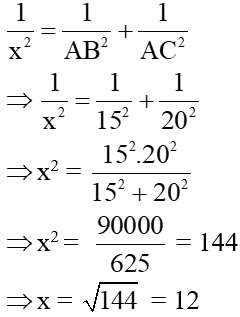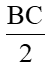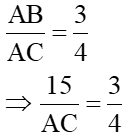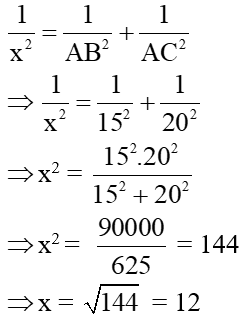Giáo án Toán lớp 9 Hình học mới nhất
Haylamdo biên soạn và sưu tầm Với mục đích giúp các Thầy / Cô giảng dạy môn Toán dễ dàng biên soạn Giáo án Toán lớp 9, VietJack biên soạn Tuyển chọn bộ Giáo án Toán lớp 9 Hình học phương pháp mới theo hướng phát triển năng lực bám sát mẫu Giáo án môn Toán chuẩn của Bộ Giáo dục. Hi vọng tài liệu Giáo án Toán 9 này sẽ được Thầy/Cô đón nhận và đóng góp những ý kiến quí báu.
Mục lục Giáo án Toán lớp 9 Hình học
Giáo án Toán 9 Chương 1: Hệ thức lượng trong tam giác vuông
- Giáo án Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Giáo án Toán 9 Luyện tập trang 69-70
- Giáo án Toán 9 Bài 2: Tỉ số lượng giác của góc nhọn
- Giáo án Toán 9 Luyện tập trang 77
- Giáo án Toán 9 Luyện tập trang 84
- Giáo án Toán 9 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
- Giáo án Toán 9 Luyện tập trang 89
- Giáo án Toán 9 Ôn tập chương 1 Hình học
Giáo án Toán 9 Chương 2: Đường tròn
- Giáo án Toán 9 Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Giáo án Toán 9 Luyện tập trang 100-101
- Giáo án Toán 9 Bài 2: Đường kính và dây của đường tròn
- Giáo án Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Giáo án Toán 9 Luyện tập trang 106
- Giáo án Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
- Giáo án Toán 9 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn.
- Giáo án Toán 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
- Giáo án Toán 9 Luyện tập trang 116
- Giáo án Toán 9 Bài 7: Vị trí tương đối của hai đường tròn
- Giáo án Toán 9 Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)
- Giáo án Toán 9 Luyện tập trang 123
- Giáo án Toán 9 Ôn tập chương 2 Hình học
Giáo án Toán 9 Chương 3: Góc với đường tròn
- Giáo án Toán 9 Bài 1: Góc ở tâm. Số đo cung
- Giáo án Toán 9 Luyện tập trang 69-70 (Tập 2)
- Giáo án Toán 9 Bài 2: Liên hệ giữa cung và dây
- Giáo án Toán 9 Bài 3: Góc nội tiếp
- Giáo án Toán 9 Luyện tập trang 75-76
- Giáo án Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
- Giáo án Toán 9 Luyện tập trang 79-80
- Giáo án Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn
- Giáo án Toán 9 Luyện tập trang 83
- Giáo án Toán 9 Bài 6: Cung chứa góc
- Giáo án Toán 9 Luyện tập trang 87
- Giáo án Toán 9 Bài 7: Tứ giác nội tiếp
- Giáo án Toán 9 Luyện tập trang 89-90
- Giáo án Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Giáo án Toán 9 Bài 9: Độ dài đường tròn, cung tròn
- Giáo án Toán 9 Luyện tập trang 95-96
- Giáo án Toán 9 Bài 10: Diện tích hình tròn, hình quạt tròn
- Giáo án Toán 9 Luyện tập trang 99-100
- Giáo án Toán 9 Ôn tập chương 3 Hình học
Giáo án Toán 9 Chương 4: Hình trụ - Hình nón - Hình cầu
- Giáo án Toán 9 Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ
- Giáo án Toán 9 Luyện tập trang 111-112-113
- Giáo án Toán 9 Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Giáo án Toán 9 Luyện tập trang 119-120
- Giáo án Toán 9 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu
- Giáo án Toán 9 Luyện tập trang 126
- Giáo án Toán 9 Ôn tập chương 4 Hình học
- Giáo án Toán 9 Bài tập ôn cuối năm
Giáo án Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
I. Mục tiêu:
Qua bài này giúp HS:
1. Kiến thức
-.Nhận biết cặp tam giác đồng dạng trong chứng minh hệ thức lượng
- Thiết lập được các hệ thức về cạnh và đường cao trong tam giác vuông và củng cố định lý Pitago.
- Vận dụng được kiến thức làm bài tập.
2. Kỹ năng
- Bước đầu vận dụng được kiến thức giải một số bài tập liên quan.
- Liên hệ được với thực tế.
3. Thái độ
- Nghiêm túc và hứng thú học tập, chú ý lắng nghe.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán, năng lực giải quyết vấn đề, năng lực hợp tác, năng lực ngôn ngữ, năng lực giao tiếp, năng lực tự học.
Phẩm chất: Tự tin, tự chủ.
II. Chuẩn bị:
- Gv : Phấn mầu, bảng phụ, thước thẳng, êke.
- Hs: Đồ dùng học tập, đọc trước bài.
III. Tiến trình dạy học:
1. Ổn định :(1 phút)
2.Kiểm tra bài cũ : (Thông qua).
3.Bài mới :
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
A – Hoạt động khởi động – 2p |
||
GV giới thiệu về chương trình hình học 9, các yêu cầu đối với môn học và các quy định khác. Trong tam giác vuông, nếu biết hai cạnh hoặc một cạnh và một góc nhọn thì có thể tính được các góc và các cạnh còn lại của tam giác đó hay không? Tiết học hôm nay chúng ta sẽ nghiên cứu vấn đề đó |
||
B – Hoạt động hình thành kiến thức |
||
|
1: Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền(12 phút) *Giao nhiệm vụ: nắm được các định lý, viết GT,KL cho các định lý, làm được các ví dụ *Hình thức hoạt động: Hđ cá nhân, cặp đôi và hoạt động nhóm *Mục tiêu: Hs nắm được quan hệ giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền GV giới thiệu các ký hiệu đồng bộ trong toàn bài học. |
||
|
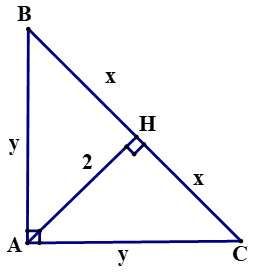
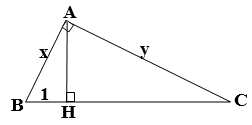
* NV1: Tìm các cặp tam giác vuông đồng dạng trong hình trên? * NV2: Nêu nội dung của định lý 1, chứng minh định lý - GV hướng dẫn HS chứng minh định lý 1 bằng “phân tích đi lên” để tìm ra điều cần chứng minh: ΔAHC ∼ ΔBAC và ΔAHB ∼ ΔCAB * NV 3: Mấu chốt của việc cm hai hệ thức trên là gì Áp dụng làm bài tập 2 tr 68 (Đưa đề bài và hình vẽ lên bảng phụ). GV: Từ kết quả định lý 1 có thể vận dụng c/m định lý Pitago Em nào chứng minh hệ thức a2 = b2 + c2. *NV4: Làm bài 2/68 |
HS vẽ hình, ghi lại các kí hiệu trên hình vẽ để sử dụng trong toàn bài học HS tìm tất cả các cặp tam giác vuông đồng dạng có trên hình vẽ. HS đọc định lý 1 và nêu GT, KL của định lý
- HS chú ý trả lời các câu hỏi để đi đến cách chứng minh định lý 1. - HS trả lời miệng, gv ghi bảng - Từ b2=ab’ và c2=ac’ cộng vế theo vế ta được điều phải chứnh minh. HS tính BC = 5 Từ đó áp dụng tính được x và y |
1. Quan hệ giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền Định lý 1: Học SGK/65 CM: Xét và có:
Hay c2=a.c’ Tương tự ta có: b2=a.b’ Bài 2/68
KQ: x = √5; y = 2√5 |
|
2. Một số hệ thức liên quan tới đường cao (15p) - Mục tiêu: HS nêu được nội dung định lí, chứng minh được định lí, vận dụng định lí làm ví dụ 2. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp, trực quan. |
||
- GV giới thiệu nội dung của định lý 2, cho một số HS nhắc lại nội dung * NV1: Chứng minh định lý - Hướng dẫn HS bắt đầu từ kết luận, dùng phân tích đi lên để xác định cần chứng minh hai tam giác vuông đồng dạng ΔAHB và ΔCHA . *NV2: làm ?1 *NV3: nghiên cứu VD 2 (Đưa đề bài và hình vẽ lên bảng phụ ) ? Đề bài yêu cầu ta tính gì? ? Trong tam giác vuông ADC ta đã biết những gì? ?Cần tính đoạn nào? Cách tính? - GV đánh giá việc thực hiện nhiệm vụ của hs. * Gv: VD 2 cho ta một cách đo gián tiếp chiều cao AC chỉ với một dụng cụ đơn giản là chiếc êke (hoặc một góc vuông quyển sách), cách đo này không dễ dàng vì người đo phải chọn một vị trí đứng thích hợp. Một cách xđ chiều cao mà người quan sát có thể đứng ở vị trí bất kìdddược nêu trong bài “Thực hành ngoài trời” ở bài 5. . |
HS nhắc lại nội dung của định lý 2 HS làm ?1 vào vở của mình, dưới sự hướng dẫn của GV. HS nghiên cứu ví dụ 2, quan sát bảng phụ và trả lời các câu hỏi của gv 1 hs lên bảng HS nhận xét bài làm trên bảng |
Định lý 2: SGK/65
CM: ?1. Xét và có:
=> ΔAHB ∼ ΔCHA
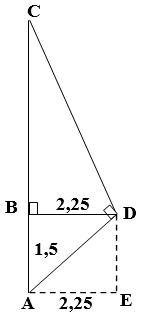
=> AH2=HB.HC Hay h2=b’.c’ Ví dụ 2: Xem SGK/66
Tính đoạn BC: Áp dụng định lý 2 ta có: BD2=AB.BC Hay 2,252=1,5.BC => BC= 2,252/1,5 = 3,375 (m) Vậy chiều cao của cây là : AC = AB + BC = 1,5+3,375 = 4,875 (m) |
C- Hoạt động luyện tập – 8 p |
||
|
*Mục tiêu: Củng cố định lí 1 và định lí 2 *Giao nhiệm vụ: Làm bài tập 1(SGK) *Cách thức hoạt động: +Giao nhiệm vụ: hoạt động cá nhân +Thực hiện nhiệm vụ: 2 Hs lên bảng trình bày Bài 1/68: a) Ta có (x+y) = √62 + 82(Đ/L Pitago) => x +y = 10 Mà 62 = 10 . x (Đ/L 1) => x = 3,6; y = 10 – 3,6 = 6,4 b) 122 = 20 . x (Đ/L 1) => x = 122 : 20 = 7,2 y = 20 – 7,2 = 12,8+Gv gọi Hs khác nhận xét bài làm của bạn rồi chốt lại vđ |
||
D - Hoạt động vận dụng - 6 Mục tiêu: HS vận dụng kiến thức đã học vào giải toán |
||
|
*Mục tiêu: Hs biết vận dụng kiến thức về quan hệ giữa cạnh và đường cao trong tam giác vuông vào làm bài tập tính toán các yếu tố của tam giác vuông *Giao nhiệm vụ: Làm bài tập : Cho tam giác vuông ABC vuông tại A, đường cao AH.Biết AB=12cm, BH = 6cm. Tính AC,BC,AH,CH *Cách thức hoạt động: +Giao nhiệm vụ: hoạt động nhóm +Thực hiện nhiệm vụ: Áp dụng định lí 1, ta có: AB2 = BH.BC => BC = Áp dụng định lý 2, ta có: AH2 = BH.CH = 6.18 => AH = √108 Áp dụng định lý Pi ta go ta có: AC = √432 +Gv yêu cầu các nhóm nhận xét kq lẫn nhau rồi chốt lại vấn đề |
||
|
E - Hoạt động hướng dẫn về nhà – 2p Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. |
||
+ Học thuộc hai định lý 1 và 2. + Làm bài tập 2 trong SGK,1,2 SBT /T 89. |
||
Giáo án Toán 9 Luyện tập trang 69-70
I. Mục tiêu:
Qua bài này giúp HS:
1. Kiến thức
- Nhắc lại được các hệ thức về cạnh và đường cao trong tam giác vuông
-Nhận biết được bài toán từ đó sử dụng kiến thức phù hợp
- Vận dụng được các hệ thức trên vào giải bài tập cơ bản.
2. Kỹ năng
- Bước đầu vận dụng được kiến thức giải một số bài tập liên quan.
- Phân tích được đề bài, nhận biết yêu cầu đề và trình bày logic, chính xác.
- Liên hệ được với thực tế.
3. Thái độ
- Nghiêm túc và hứng thú học tập, chú ý lắng nghe.
- Có thái độ tích cực, chủ động làm bài tập.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán, năng lực giải quyết vấn đề, năng lực hợp tác, năng lực ngôn ngữ, năng lực giao tiếp, năng lực tự học.
Phẩm chất: Tự tin, tự chủ
II. Chuẩn bị:
- Gv : Phấn mầu, bảng phụ, thước thẳng, êke.
- Hs: Đồ dùng học tập, học bài
III. Tiến trình dạy học:
1. Ổn định (1 phút)
2. Nội dung
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
|
Hoạt động 1: Khởi động + Chữa bài tập – 10p - Mục tiêu: HS vận dụng được kiến thức đã học vào các bài toán có hình vẽ sẵn., các bài toán định lượng. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp, trực quan. |
||
GV nêu y/c kiểm tra: + HS1 phát biểu đlý 1, 2 và chữa bài tập 3a SBT + HS 2: phát biểu đlý 3, 4 và chữa bài tập 4a SBT GV nx, cho điểm |
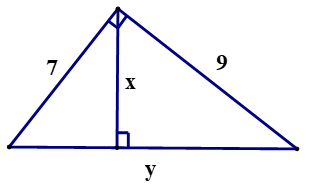
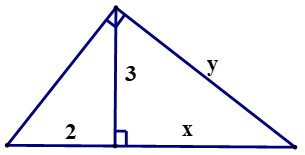
2 HS lên bảng kiểm tra + HS1 phát biểu đlý 1, 2 và chữa bài tập 3a SBT Ta có: + y2 = 72 + 92 = 130 ( Đ/l Pitago) => y = √130 + x.y = 7.9 (đ/l 3) => x = + HS 2: phát biểu đlý 3, 4 và chữa bài tập 4a SBT Ta có: +) 32 = 2.x ( Đlý 2) => x = +) y2 = x(x + 2)(Đlý 1) => y2 = 4,5(4,5 + 2) => y2 = 4,5. 6,5 => y2 = => y = HS lớp nx, chữa bài |
1. Bài 3a(SBT):
Ta có: + y2 = 72 + 92 = 130 ( Đ/l Pitago) => y = √130 + x.y = 7.9 (đ/l 3) => x = 2. Bài 4a(SBT) :
Ta có: +) 32 = 2.x ( Đlý 2) => x = +) y2 = x(x + 2)(Đlý 1) => y2 = 4,5(4,5 + 2) => y2 = 4,5. 6,5 => y2 = => y = |
|
Hoạt động 2: Luyện tập – 32p - Mục tiêu: HS phân tích đề bài, vận dụng kiến thức đã học vào các bài toán định lượng, lưu ý các bài toán bổ sung thêm hình vẽ bằng nhiều cách khác nhau. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp, trực quan, hoạt động nhóm. |
||
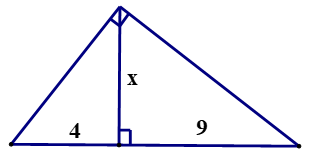
| GV y/c HS làm bài 8 (SGK – tr70) GV: Trong câu a, x là độ dài đường cao t/ư với cạnh huyền. Còn 4, 9 là độ dài 2 hình chiếu của 2 cgv trên cạnh huyền. ? Để tìm x ta áp dụng hệ thức nào? GV: Vận dụng hệ thức này hãy tìm x? GV: (điền tên các đỉnh lên hình vẽ). Trong câu b các em có nx gì về tam giác vuông này? ? Vậy khi đó đường cao sẽ có tính chất gì? Và x = ? GV: nêu cách tìm y? c. GV điền các đỉnh của tam giác ? Để tìnm x ta làm ntn? GV: Nêu cách tìm y? GV: ta có thể tìm y bằng cách nào khác? GV y/c HS làm bài 4b SBT GV: Từ hình vẽ bài toán đã cho biết những gì? GV: Với GT như vậy ta có thể tìm được cạnh nào? GV: Như vậy vABC đã biết độ dài của 2 cạnh góc vuông. Vậy ta có thể tìm y được không? Bằng kiến thức nào? GV: ta có thể tìm x bằng những cách nào? GV nx bài làm của HS GV y/c HS làm bài 5a SBT ? Hãy tính AB? GV: ta có thể tính được độ dài của cạnh nào? GV: Tính được BC ta sẽ suy ra được độ dài của đoạn nào? GV: Hãy tính AC GV nx bài làm của HS và nhấn mạnh lại các định lý và hệ thức |
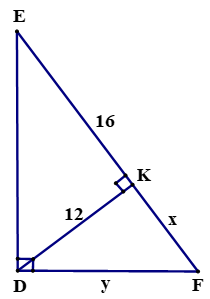
HS làm bài 8 (SGK – tr70) HS: Ta áp dụng hệ thức của đlý 2: h2 = b’.c’ HS: x2 = 4.9 (Đ/lý 22) => x2 = 36 => x = √36 = 6 HS: Tam giác vuông này có 2 cạnh góc vuông = nhau nên là tam giác vuông cân HS: AH = BH = CH = => x = 2 HS1: Áp dụng định lý Pytago ta có: AB2 = AH2 + BH2 => y2 = 22 + 22 = 4 + 4 => y2 = 8 => y = √8 = 2√2 HS 2: Áp dụng đlý 1 ta có: AB2 = BC.BH => y2 = (2 + 2). 2 = 8 => y2 = 8 => y = √8 = 2√2 HS: + Trong ∆v DEF có DK ⊥ EF => DK2 = KE.KF (Đlý 2) => 122 = 16.x => x = 144 : 16 = 9 HS1: DF2 = DK2 + KF2 (Định lý Pytago) y2 = 122 + 92 = 144 + 81 = 225 => y = √225 = 15 HS2: Ta có: DF2 = EF.KF (đlý 1) => y2 = (16 + 9).9 = 25.9 => y2 = 225 => y = √225 = 15 HS lớp nx, chữa bài HS suy nghĩ làm bài 4b SBT HS: AB = 15 và HS: Ta có thể tính được AC
=> 3AC = 15.4 = 60 => AC = 20 HS: Áp dụng đlý Pytago ta có: BC2 = AB2 + AC2 => y2 = 152 + 202 => y2 = 225 + 400 = 625 => y = √625 = 25 HS: + Áp dụng đlý 3 ta có: x.y = 15.20 <=> x.25 = 300 <=> x = 300 : 25 = 12 Hoặc Áp dụng đlý 4 ta có:
HS lớp nx, chữa bài HS suy nghĩ làm bài 5a SBT HS: Áp dụng định lý Pytago trong ∆v AHB ta có: AB2 = AH2 + BH2 => AB2 = 162 + 252 = 256 + 625 = 881 => AB = √881 HS: Ta có thể tính được BC dựa vào đlý 1 AB2 = BC.BH => 881 = BC. 25 => BC = 881 : 25 = 35,24 HS:=> CH = BC – BH => CH = 35,24 – 25 => CH = 10,24 HS: ta có: AB2 + AC2 = BC2 => AC2 = 35,242 – 881 => AC2 = 360,8576 => AC ≈ 18,99 HS hoàn thành bài tập vào vở |
3. Bài 8 (SGK – tr70) a.
Ta có: x2 = 4.9 (Đ/lý 22) => x2 = 36 => x = √36 = 6 b.
+ Xét ∆ ABC có: AB = AC => ∆ ABC vuông cân tại A Lại có: AH ⊥ BC tại H => AH đồng thời là đường trung tuyến ứng với cạnh huyền BC => AH = BH = CH = => x = 2 + Trong ∆v AHB có AB2 = AH2 + BH2 (Đlý Pytago) => y2 = 22 + 22 = 4 + 4 => y2 = 8 => y = √8 = 2√2 * Cách 2: Áp dụng đlý 1 ta có: AB2 = BC.BH => y2 = (2 + 2). 2 = 8 => y2 = 8 => y = √8 = 2√2 c.
+ Trong ∆v DEF có DK ⊥ EF => DK2 = KE.KF (Đlý 2) => 122 = 16.x => x = 144 : 16 = 9 + Lại có: DF2 = DK2 + KF2 (Định lý Pytago) => y2 = 122 + 92 = 144 + 81 = 225 => y = √225 = 15 * Cách 2: Ta có: DF2 = EF.KF (đlý 1) => y2 = (16 + 9).9 = 25.9 => y2 = 225 => y = √225 = 15 4. Bài 4b(SBT)
+ Ta có:
=> 3AC = 15.4 = 60 => AC = 20 + Áp dụng đlý Pytago ta có: BC2 = AB2 + AC2 => y2 = 152 + 202 => y2 = 225 + 400 = 625 => y = √625 = 25 + Áp dụng đlý 3 ta có: x.y = 15.20 => x.25 = 300 => x = 300 : 25 = 12 * Cách 2: Áp dụng đlý 4 ta có:
5. Bài 5a (SBT): Áp dụng định lý Pytago trong ∆v AHB ta có: AB2 = AH2 + BH2 => AB2 = 162 + 252 = 256 + 625 = 881 => AB = √881 + Ta có: AB2 = BC.BH (đlý 1) => 881 = BC. 25 => BC = 881 : 25 = 35,24 => CH = BC – BH => CH = 35,24 – 25 => CH = 10,24 + Ta có: AB2 + AC2 = BC2 => AC2 = 35,242 – 881 => AC2 = 360,8576 => AC ≈ 18,99 |
|
Hoạt động 3: Tìm tòi, mở rộng – 2p - Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Kĩ thuật sử dụng: Kĩ thuật viết tích cực, |
||
|
- Nắm vững các hệ thức đã học - BTVN: 5b,c; 8; 9; 10; 12; 15; 16; 17; 18; 19; 20 (SBT) - Tiết sau tiếp tục LT |
||

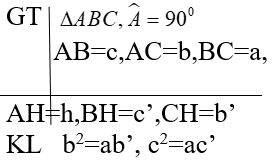
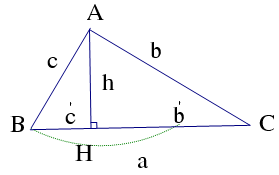
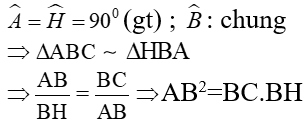
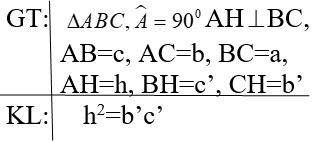
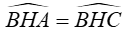 = 900 (gt)
= 900 (gt)
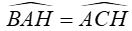 ( cùng phụ với góc ABH )
( cùng phụ với góc ABH )
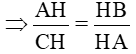
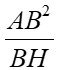 = 24 => CH = BC - BH = 18
= 24 => CH = BC - BH = 18
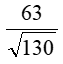
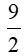 = 4,5
= 4,5
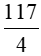
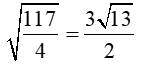
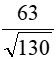
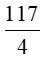
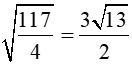
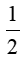 BC
BC