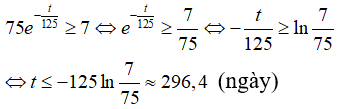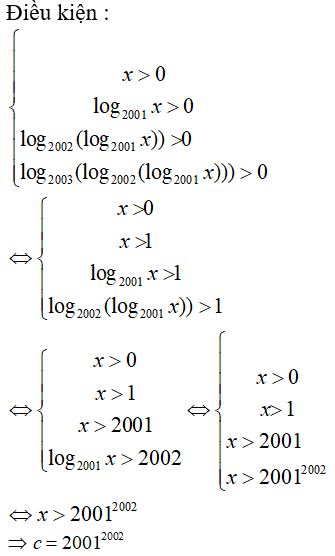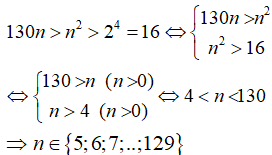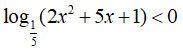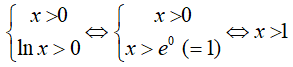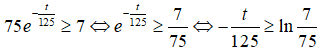Trắc nghiệm Bất phương trình mũ và bất phương trình lôgarit có đáp án năm 2023 (phần 2)

---

Trắc nghiệm Bất phương trình mũ và bất phương trình lôgarit có đáp án năm 2023 (phần 2)

Với bộ Trắc nghiệm Bất phương trình mũ và bất phương trình lôgarit có đáp án năm 2023 (phần 2) sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.

Câu 1: Giải bất phương trình

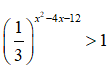
A. x < -6 hoặc x > 2    C. x < -2 hoặc x > 6

B. -6 < x < 2    D. -2 < x < 6

Hiển thị đáp án

(1/3)^{x2 - 4x + 12} > 1 ⇔ x² - 2x - 12 < 0 (vì (1/3) < 1) ⇔ -2 < x < 6

Câu 2: Giải bất phương trình 2.4^{x + 1} < 16^2x

A. x > 1    B. x < 1    C. x > 1/2    D. x < 1/2

Hiển thị đáp án

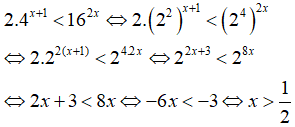
Câu 3: Giải bất phương trình 2^x.3^x ≤ 36

A. x ≤ 2    B. x ≤ 3    C. x ≤ 6    D. x ≤ 4

Hiển thị đáp án

2^x.3^x ≤ 36 ⇔ 6^x ≤ 6² ⇔ x ≤ 2

Câu 4: Giải bất phương trình 7.3^{x + 1} + 5^{x + 3} ≤ 3^{x + 4} + 5^{x + 2}

A. x ≤ -1   B. x ≥ -1    C. x ≤ 0    D. x ≥ 0

Hiển thị đáp án

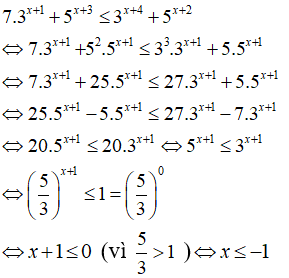
Câu 5: Tìm tập nghiệm của bất phương trình

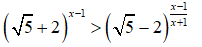
A. (-1; 1)   C. (-∞; -1) ∪ (-1; 1)

B. (-1; -1) ∪ (1; +∞)    D. (-∞; -2) ∪ (1; +∞)

Hiển thị đáp án

Nhận thấy (√5 + 2)(√5 - 2) = 1 hay √5 - 2 = (√5 + 2)^-1 nên bất phương trình đã cho tương đương với

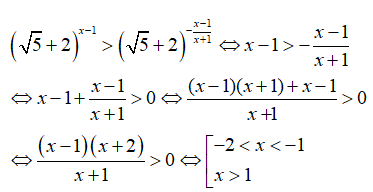
Tập nghiệm là (-2; -1) ∪ (1; +∞)

Câu 6: Tìm tập nghiệm của bất phương trình

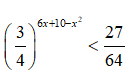
A. (-∞; -1) ∪ (7; +∞)   C. (7; +∞)

B. (-1; 7)   D. (-7; 1)

Hiển thị đáp án

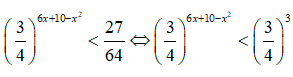
⇔ 6x + 10 - x² > 3 ⇔ x² - 6x - 7 < 0 ⇔ -1 < x < 7.

Chọn đáp án C

Câu 7: Giải bất phương trình

Hiển thị đáp án

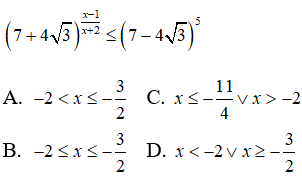
Nhận xét rằng (7 + 4√3)(7 - 4√3) = 1 hay 7 - 4√3 = (7 + 4√3)^-1

Do đó bất phương trình đã cho tương đương với

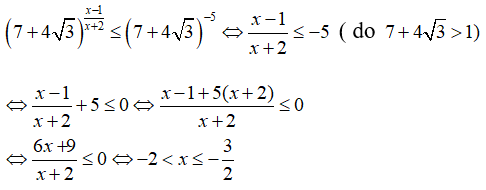
Chọn đáp án A.

Câu 8: Giải bất phương trình 3^{2x - 1} < 11^{3 - x}

Hiển thị đáp án

Lấy lôgarit theo cơ số 3 hai vế của bất phương trình , ta được :

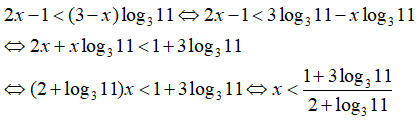
Chọn đáp án D.

Câu 9: Giải bất phương trình 2016^x + 2016^{1 - x} ≤ 2017

A. 1 ≤ x ≤ 2016    C. x ≤ 1 hoặc x ≥ 2016

B. 0 ≤ x ≤ 1     D. x ≤ 0 hoặc x ≥ 1

Hiển thị đáp án

Ta có:

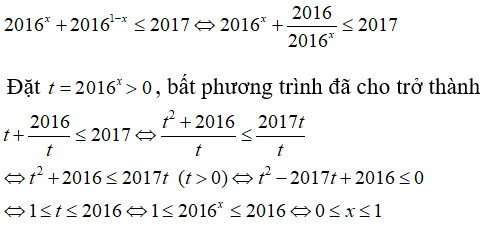
Chọn đáp án B

Câu 10: Tìm tập nghiệm của bất phương trình log_1/5(x² + 4x) ≥ -1

A. ∅    C. (-∞; -5] ∪ [1; +∞)

B. [-5; 1]   D. [-5; -4) ∪ (0; 1]

Hiển thị đáp án

Bất phương trình đã cho tương đương với

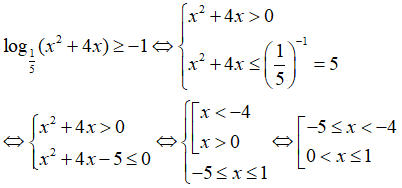
Chọn đáp án D.

Câu 11: Tìm tập nghiệm của bất phương trình log(x - 21) < 2 - logx

A. (-4; 25)     B. (0; 25)    C. (21; 25)    D. (25; +∞)

Hiển thị đáp án

Điều kiện x > 21. Khi đó:

log(x - 21) < 2 - logx ⇔ log(x - 21) + logx < 2

⇒ log[x(x - 21)] < 2 ⇒ x(x - 21) < 10²

⇔ x² - 21x - 100 < 0

⇔ -4 < x < 25

Kết hợp điều kiện x > 21, ta được 21 < x < 25.

Chọn đáp án C.

Nhận xét. Nhiều bài toán quen thuộc như tìm miền xác định của hàm số, xét tính đơn điệu, cực trị,… có thể dẫn đến việc phải giải các bất phương trình mũ, lôgarit. Dưới đây là một số ví dụ.

Câu 12: Tìm miền xác định của hàm số

Hiển thị đáp án

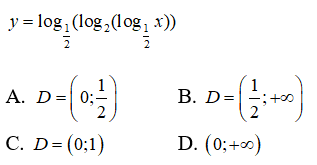
Hàm số xác định khi

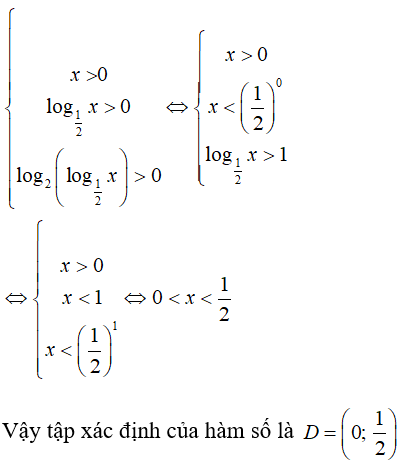
Chọn đáp án A.

Câu 13: Tìm các khoảng đồng biến của hàm số y = x²lnx

Hiển thị đáp án

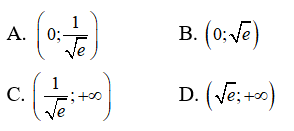
Tập xác định: D = (0; +∞)

y' = 2xlnx + x².1/x = x(2lns + 1).

Ta thấy:

y' > 0 ⇔ x(2lnx + 1) > 0 ⇔ 2lnx + 1 > 0 (vì x > 0)

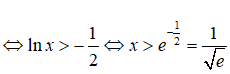
Từ đó khoảng đồng biến của hàm số là

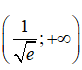
Chọn đáp án C.

Câu 14: Một tàu vũ trụ được cung cấp bởi một nguồn điện đồng vị phóng xạ plutoni-238. Công suất đầu ra của nguồn điện này được ước lượng bởi

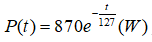
trong đó t là số năm kể từ khi con tàu hoạt động. Biết rằng để các thiết bị trên tàu hoạt động bình thường, nguồn cần cung cấp công suất tối thiểu là 600W. Hỏi con tàu đủ điện để các thiết bị hoạt động bình thường trong thời gian bao lâu ?

A. 45 năm    B. 47 năm   C. 48 năm   D. 50 năm

Hiển thị đáp án

Con tàu hoạt động bình thường khi

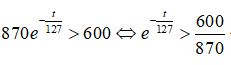
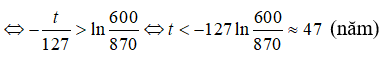
Chọn đáp án B

Câu 15: Dân số Việt Nam năm 2015 là 91,71 triệu người. Giả sử trong 5 năm tỉ lệ tăng dân số là không đổi. Hỏi tỉ lệ này có thể nhận giá trị tối đa là bao nhiêu để dân số Việt Nam năm 2020 không vượt quá 96,5 triệu người (làm tròn kết quả đến phần chục nghìn) ?

A. 1,08%    B. 0,91%   C. 1,06%   D. 1,02%

Hiển thị đáp án

Giả sử tỉ lệ tăng dân số trong 5 năm đó từ 2015 đến 2020 là k không đổi. Điều kiện của đầu bài là :

91,71.e^5k ≤ 96,5

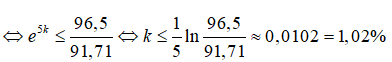
Vậy tỉ lệ tăng dân số tối đa là 1,02%.

Chọn đáp án D.

Câu 16: Giá trị của một chiếc xe ô tô sau t năm được ước lượng bằng công thức G(t) = 600e^-0,12t (triệu đồng). Để bán lại xe với giá trừ 200 triệu đến 300 triệu đồng, người chủ phải bán trong khoảng thời gian nào kể từ khi mua (làm tròn kết quả đến hàng phần mười của năm)?

A. Từ 2,5 đến 4,0 năm   C. Từ 4,0 đến 6,2 năm

B. Từ 4,0 đến 9,2 năm   D. Từ 5,8 đến 9,2 năm

Hiển thị đáp án

Yêu cầu đề bài : 200 ≤ 600e^-0,12t ≤ 300

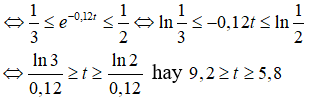
Câu 17: Giải bất phương trình

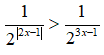
A. x < 0   B. x > 0   C. x < 2/5   D. x > 2/5

Hiển thị đáp án

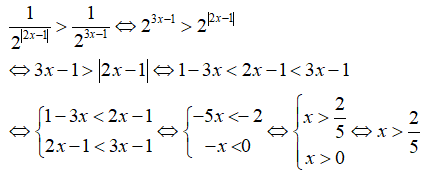
Câu 18: Tìm tập nghiệm của bất phương trình

Hiển thị đáp án

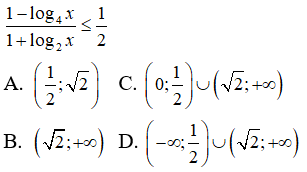
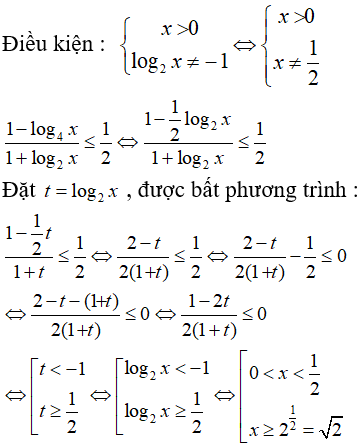
Câu 19: Miền xác định của hàm số y = log₂₀₀₄(log₂₀₀₃(log₂₀₀₂(log₂₀₀₁x))) là khoảng (c; +∞) . Xác định giá trị của c.

A. 2001²⁰⁰²   B. 2002²⁰⁰³    C. 2003²⁰⁰⁴    D. 2001^20022003

Hiển thị đáp án

Câu 20: Có bao nhiêu số nguyên dương n thỏa mãn điều kiện (130n)⁵⁰ > n¹⁰⁰ > 2²⁰⁰ ?

A. 7   B. 12   C. 65   D. 125

Hiển thị đáp án

Lấy căn bậc 50 mỗi vế của bất phương trình ta nhận được

Từ đó có 125 số nguyên dương n thỏa mãn điều kiện đã cho

Câu 21: Giải bất phương trình 5^{4x - 6} > 3^{3x - 4}

Hiển thị đáp án

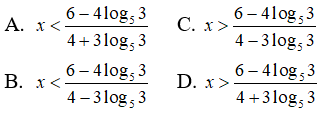
Lấy lôgarit theo cơ số 5 hai vế của bất phương trình, ta được :

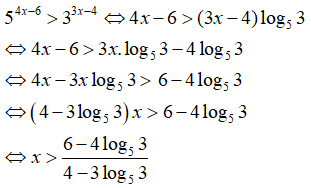
Câu 22: Trong các số dương x thỏa mãn logx ≥ log2 + (1/2)logx

A. Số có giá trị lớn nhất là 1    C. số có giá trị lớn nhất là 4

B. Số có giá trị nhỏ nhất là 1    D. số có giá trị nhỏ nhất là 4

Hiển thị đáp án

Ta có

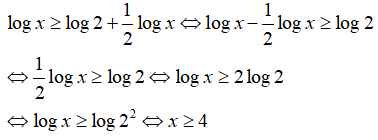
Số x nhỏ nhất là 4

Câu 23: Giải bất phương trình log₅(2x - 4) < log₅(x + 3)

A. 2 < x < 7    B. -3 < x < 7    C. -3 < x < 2    D. x < 7

Hiển thị đáp án

log₅(2x - 4) < log₅(x + 3)

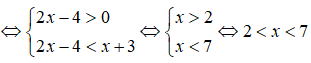
Câu 24: Giải bất phương trình ln(x^x - 2x - 2) < 0

A. -1 ≥ x ≥ 3    C. x ∞[-1; 1 - √3) ∪ (1 + √3)

B. -1 - √3 < x < 1 + √3     D. x ∞ (1 + √3), 3]

Hiển thị đáp án

Điều kiện

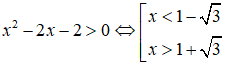
Khi đó BPT ⇔ x² - 2x - 2 ≤ e⁰ = 1 ⇔ x² - 2x - 3 ≤ 0 ⇔ -1 ≤ x ≤ 3

Kết hợp được tập nghiệm: (1 + √3; 3)

Câu 25: Giải bất phương trình

Hiển thị đáp án

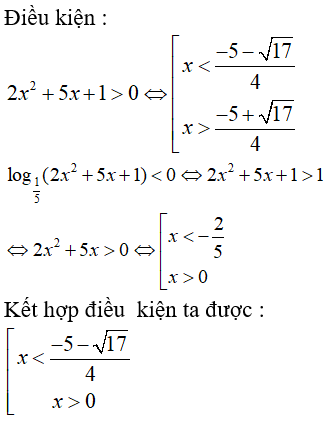
Câu 26: Giải bất phương trình logx + log(x + 9) > 11

A. 0 < x < 3   C. x < 1 hoặc x > 2

B. x < 0 hoặc x > 3   D. 0 < x < 1 hoặc 2 < x < 3

Hiển thị đáp án

Điều kiện x > 0. Khi đó bất phương trình đã cho tương đương với

log[x(x + 9)] > 1 ⇔ x(x + 9) > 10 ⇔ x² + 9x - 10 > 0

⇔ x < -10 hoặc x > 1 ⇔ x > 1 (do x > 0)

Câu 27: Giải bất phương trình 3^{log₂(x2 - 3x + 2)} > 3

A. 0 < x < 3    C. x < 1 hoặc x > 2

B. x < 0 hoặc x > 3    D. 0 < x < 1 hoặc 2 < x < 3

Hiển thị đáp án

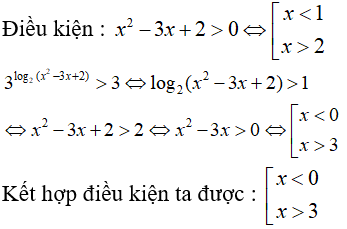
Câu 28: Tìm miền xác định của hàm số y = ln(lnx)

A. D = (e; +∞)    B. D = [e; ∞)   C. D = (0; +∞)    D. D = (1; +∞)

Hiển thị đáp án

Điều kiện

Câu 29: Tìm khoảng đồng biến của hàm số y = xlnx

A. (0; 1/e)    B. (0; e)   C. (1/e; +∞)   D. (e; +∞)

Hiển thị đáp án

Tập xác định: (0; +∞).

Câu 30: Một vệ tinh cần một nguồn điện có công suất 7W (oát) để hoạt động hết công năng. Nó được cung cấp bởi một nguồn điện đồng vị phóng xạ có công suất đầu ra P xác định bởi công thức

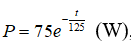
trong đó t là thời gian tính bằng ngày. Hỏi vệ tinh đó hoạt động hết công năng trong khoảng thời gian bao lâu kể từ ngày bắt đầu vận hành?

A. 128,7 ngày   B. 250 ngày   C. 296,4 ngày    D. 365,5 ngày

Hiển thị đáp án

Vệ tinh hoạt động hết công năng khi