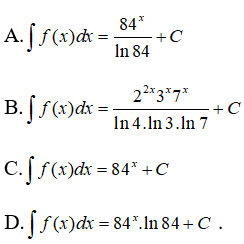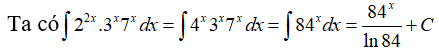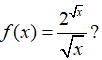Trắc nghiệm Nguyên hàm có đáp án năm 2023 (phần 2)
Trắc nghiệm Nguyên hàm có đáp án năm 2023 (phần 2)
Với bộ Trắc nghiệm Nguyên hàm có đáp án năm 2023 (phần 2) sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.
Trắc nghiệm Giải tích 12 Bài 1 (có đáp án): Nguyên hàm (phần 1)
Câu 1:
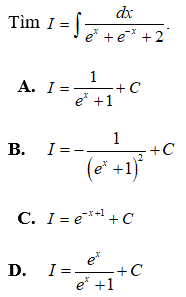
Đặt u = ex + 1 ⇒ u' = ex. Ta có
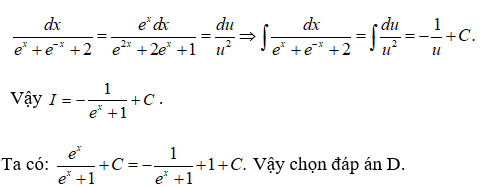
Câu 2: Trong các hàm số sau hàm số nào không phải là một nguyên hàm của f(x) = cosxsinx ?
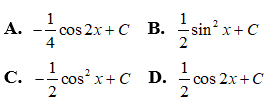
Cách 1.
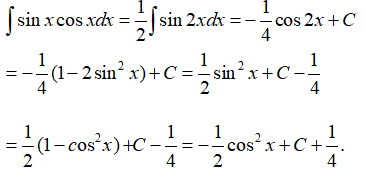
Cách 2. Sử dụng phương pháp biến đổi số ta có:
Đặt u = cosx thì u’ = -sinx và ∫sinxcosxdx = -∫u.u'dx = -∫udu
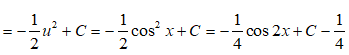
Vậy chọn đáp án D.
Câu 3: Tìm I=∫(3x2 - x + 1)exdx
A. I = (3x2 - 7x +8)ex + C B. I = (3x2 - 7x)ex + C
C. I = (3x2 - 7x +8) + ex + C D. I = (3x2 - 7x + 3)ex + C
Sử dụng phương pháp tính nguyên hàm từng phần ta có:
Đặt u = 3x2 - x + 1 và dv = exdx ta có du = (6x - 1)dx và v = ex . Do đó:
∫(3x2 - x + 1)exdx = (3x2 - x + 1)ex - ∫(6x - 1)exdx
Đặt u1 = 6x - 1; dv1 = exdx Ta có: du1 = 6dx và v1 = ex .
Do đó ∫(6x - 1)exdx = (6x - 1)ex - 6∫exdx = (6x - 1)ex - 6ex + C
Từ đó suy ra
∫(3x2 - x + 1)exdx = (3x2 - x + 1)ex - (6x - 7)ex + C = (3x2 - 7x + 8)ex + C
Vậy chọn đáp án A.
Câu 4:
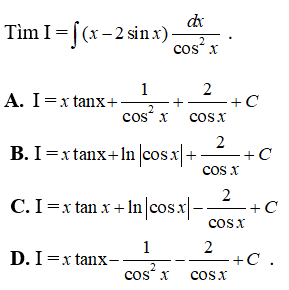
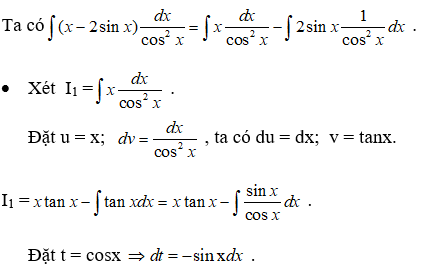
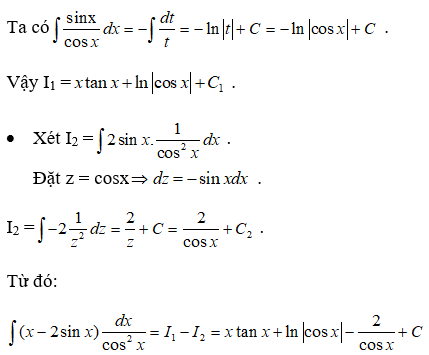
Vậy chọn đáp án C.
Câu 5: Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc
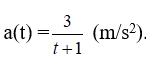
Vận tốc ban đầu của vật là 6m/s. Vận tốc của vật sau 10 giây xấp xỉ bằng
A. 10m/s B. 11m/s C. 12m/s D. 13m/s.
Vận tốc của vật bằng
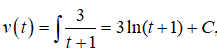
với t = 0 ta có v(0)= C = 6 nên phương trình vận tốc của chuyển động là :
v(t) = 3ln(t + 1) + 6 (m/s)
khi đó v(10) = 3ln11 + 6 ≈ 13 (m/s) .
Vậy chọn đáp án D.
Câu 6: Tìm I = ∫cos(4x + 3)dx .
A. I = sin(4x + 2) + C B. I = - sin(4x + 3) + C
C. I = (1/4).sin(4x + 3) + C D. I = 4sin(4x + 3) + C
Đặt u = 4x + 3
⇒ du = 4dx ⇒ dx = 1/4 du và cos(4x+3)dx được viết thành
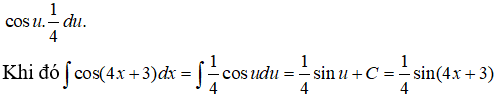
Câu 7: Trong các mệnh đề sau mệnh đề nào nhận giá trị đúng?
A. Hàm số y = 1/x có nguyên hàm trên (-∞; +∞).
B. 3x2 là một số nguyên hàm của x3 trên (-∞; +∞).
C. Hàm số y = |x| có nguyên hàm trên (-∞;+∞).
D. 1/x + C là họ nguyên hàm của lnx trên (0;+∞).
Dựa vào định lí: Mọi hàm số liên tục trên K đều có nguyên
hàm trên K. Vì y = |x| liên tục trên R nên có nguyên hàm trên R .
Phương án A sai vì y=1/x không xác định tại x=0 ∈ (-∞;+∞).
Phương án B sai vì 3x2 là đạo hàm của x3.
Phương án D sai vì 1/x là đạo hàm của lnx trên (0; +∞).
Vậy chọn đáp án C.
Câu 8: Hàm số nào dưới đây không phải là một nguyên hàm của f(x)=2x-sin2x ?
x2 + (1/2).cos2x B. x2 + cos2 x C. x2 - sin2x D. x2 + cos2x .
Ta có
∫(2x-sin2x)dx=2∫xdx-∫sin2xdx
D không phải là nguyên hàm của f(x). Vậy chọn đáp án D.
Câu 9: Tìm nguyên hàm của
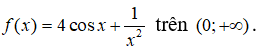
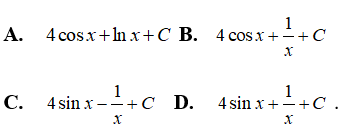
Với x ∈ (0; +∞) ta có
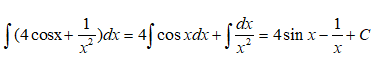
Vậy chọn đáp án C.
Câu 10:
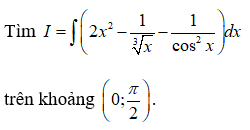
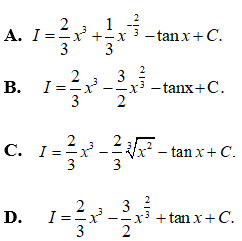
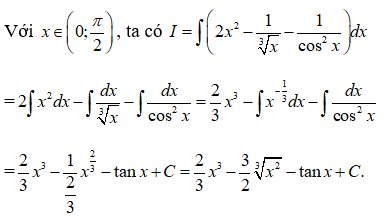
Vậy chọn đáp án B.
Ghi chú. Yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.
Câu 11: Tìm I = ∫x.e3xdx
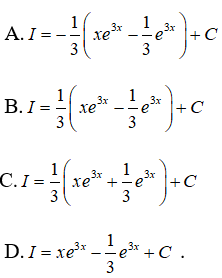
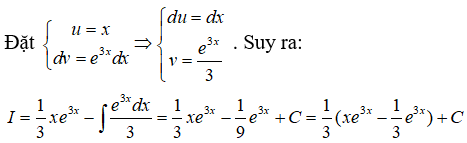
Câu 12: Hàm số nào sau đây không phải là một nguyên hàm của:
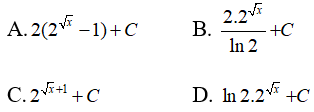
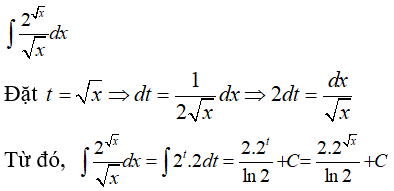
Câu 13: Họ nguyên hàm của hàm số
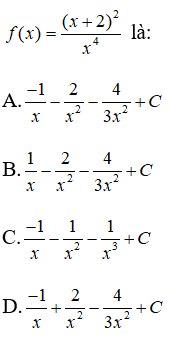
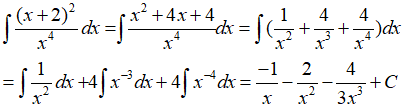
Câu 14: Họ nguyên hàm của hàm số
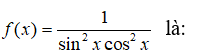
A. cot2x + C B. -2cot2x + C C. 2cot2x + C D. -cot2x + C .
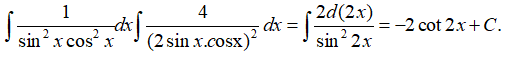
Câu 15: Hàm số nào dưới đây không là nguyên hàm của
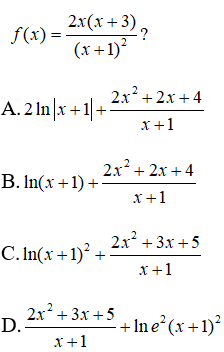
Câu 16: Họ nguyên hàm của hàm số f(x) = (2 tanx + cotx)2 là:
A. 2tanx - cotx - x + C B. 4tanx + cotx - x + C
C. 4tanx - cotx + x + C D. 4tanx - cotx - x + C
∫(2tanx + cotx)2dx = ∫(4tan2x + 2tanx.cotx + cot2x)dx
= ∫ [4(tan2x + 1) + (cot2x + 1) - 1]dx
= 4tanx = cotx - x + C
Câu 17: Biết rằng: f'(x) = ax + b/x2, f(-1) = 2, f(1) = 4, f'(1) = 0
Giá trị biểu thức ab bằng :
A.0 B.1 C.-1 D. 1/2 .
Ta có:
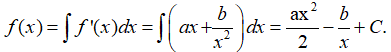
Từ điều kiện đã cho ta có phương trình sau:
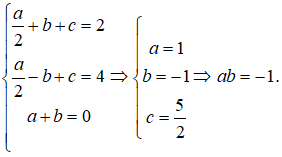
Câu 18: Cho các hàm số:
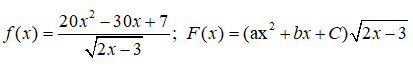
với x > 3/2. Để F(x) là một nguyên hàm của f(x) thì giá trị của a,b,c lần lượt là:
A. a = 4; b = 2; c= 1 B. a = 4; b = -2; c = -1
C. a = 4; b = -2; c = 1 D. a = 4; b = 2; c = -1 .
Ta có:
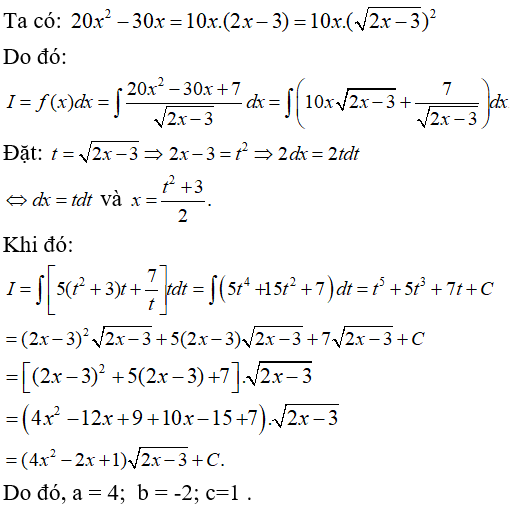
Câu 19: Một đám vi khuẩn tại ngày thứ t có số lượng là N(t). Biết rằng
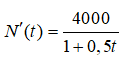
và lúc đầu đám vi khuẩn có 250000 con. Sau 10 ngày số lượng vi khuẩn xấp xỉ bằng:
A. 264334 B. 263334 C.264254 D.254334.
Số lượng vi khuẩn tại ngày thứ t bằng
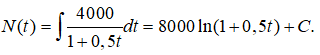
Với t = 0 ta có: N(0) = 250000,
Vậy N(t) = 8000.ln(1 + 0,5t) + 250000
khi đó N(10) ≈ 264334.
Câu 20: Tìm I = ∫sin5xcosxdx .
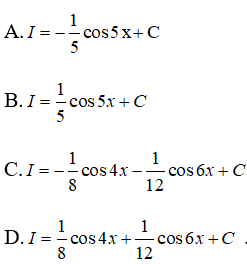
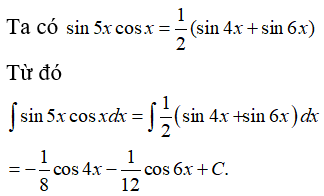
Câu 21:
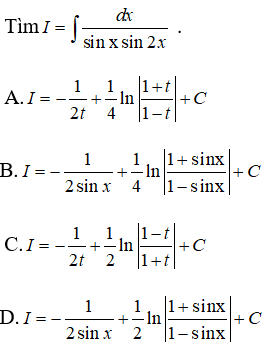
Ta biến đổi để thu được:
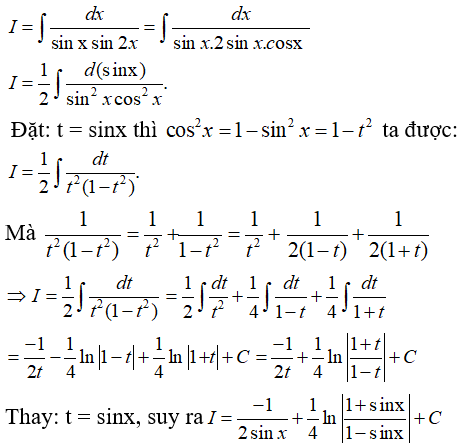
Câu 22: Tìm nguyên hàm của hàm số f(x) = 22x.3x.7x .
