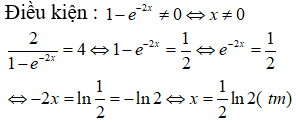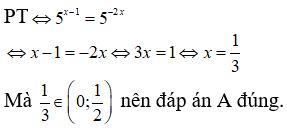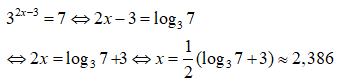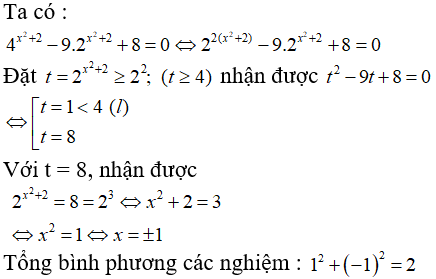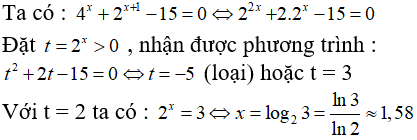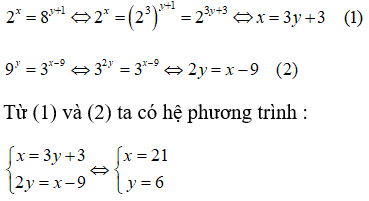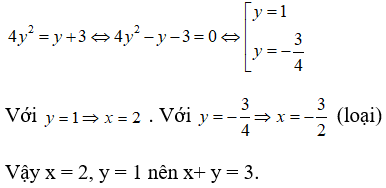Trắc nghiệm Phương trình mũ và phương trình lôgarit có đáp án năm 2023 (phần 2)

---

Trắc nghiệm Phương trình mũ và phương trình lôgarit có đáp án năm 2023 (phần 2)

Với bộ Trắc nghiệm Phương trình mũ và phương trình lôgarit có đáp án năm 2023 (phần 2) sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.

Câu 1: Giải phương trình 10^x = 0,00001

A. x = -log4    B. x = -log5    C. x = -4    D. x = -5

Hiển thị đáp án

10^x = 0,00001 ⇔ 10^x = 10^-5 ⇔ x = -5

Câu 2: Giải phương trình

Hiển thị đáp án

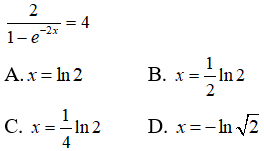
Câu 3: Cho phương trình

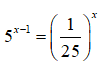
Nghiệm của phương trình này nằm trong khoảng nào dưới đây ?

Hiển thị đáp án

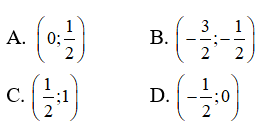
Câu 4: Giải phương trình 3^{2x - 3} = 7 . Viết nghiệm dưới dạng thập phân, làm tròn đến hàng phần nghìn.

A. x ≈ 2,38   B. x ≈ 2,386    C. x ≈ 2,384   D. x ≈ 1,782

Hiển thị đáp án

Câu 5: Tính tổng bình phương các nghiệm của phương trình 4^{x2 + 2} - 9.2^{x2 + 2} + 8 = 0

A. 2   B. 4   C. 17   D. 65

Hiển thị đáp án

Câu 6: Giải phương trình 4^x + 2^{x + 1} - 15 = 0. Viết nghiệm tìm được dưới dạng thập phân, làm tròn đến hàng phần trăm

A. x ≈ 0,43     B. x ≈ 0,63    C. x ≈ 1,58    D. x ≈ 2,32

Hiển thị đáp án

Câu 7: Giả sử x là nghiệm của phương trình

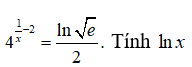
A. 0   B. ln3    C. –ln3    D. 1/ln3

Hiển thị đáp án

Để ý rằng

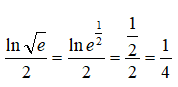
nên phương trình đã cho tương đương với

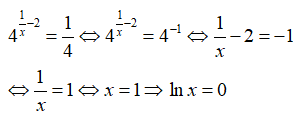
Chọn đáp án A.

Câu 8: Tính tích tất cả các nghiệm của phương trình 3^{2x2 + 2x + 1} - 28.3^{x2 + x} + 9 = 0

A. -4    B. -2    C. 2    D. 4

Hiển thị đáp án

Ta có: 3^{2x2 + 2x + 1} -28.3^{x2 + x} + 9 = 0 ⇔ 3.3^{2(x2 + x)} - 28.3^{x2 + x} + 9 = 0

Đặt t = 3^x2 + x > 0 nhận được phương trình

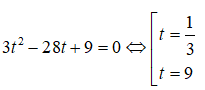
Với t = 1/3 = 3^-1 được 3^{x2 + x} = 3^-1 ⇔ x² + x + 1 = 0(vô nghiệm)

Với t = 9 được phương trình 3^{x2 + x} = 9 = 3² ⇔ x² + x = 2

x² + x - 2 = 0 ⇔ x -2 hoặc x = 1

Tích của hai nghiệm này bằng -2.

Chọn đáp án B

Câu 9: Tìm nghiệm của phương trình 2^{x - 1} = 3^{1 - 2x}

Hiển thị đáp án

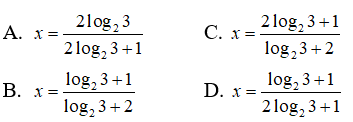
Có nhiều cách biến đổi phương trình này. Tuy nhiên, nhận thấy các biểu thức trong các phương án đều chứa log₂3 , nên ta lấy lôgarit cơ số 2 hai vế của phương trình để nhận được:

(x - 1) = (1 - 2x)log₂3

⇔ x - 1 = log₂3 - 2xlog₂3

⇔ x + 2xlog₂3 = log₂3 + 1

⇔ x(2log₂3 + 1) = log₂3 + 1

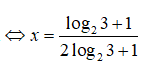
Chọn đáp án D

Câu 10: Giải phương trình (x² - 2x)lnx = lnx³

A. x = 1, x = 3    B. x = -1, x = 3     C. x = ±1, x = 3    D. x = 3

Hiển thị đáp án

Điều kiện x > 0. Khi đó phương trình đã cho tương đương với

(x² -2x)lnx = 3lnx ⇔ (x² - 2x + 3)lnx = 0

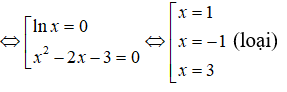
Vậy phương trình có hai nghiệm là x = 1, x = 3 .

Chọn đáp án A.

Chú ý. Sai lầm thường gặp là quên điều kiện dẫn đến không loại được nghiệm x = -1 và chọn phương án nhiễu C.

Thậm chí, có thể học sinh biến đổi (x² - 2x)lnx = 3lnx ⇔ x² -2x = 3(giản ước cho lnx) dẫn đến mất nghiệm x = 1 và chọn phương án nhiễu D.

Câu 11: Nếu log₇(log₃(log₂x)) = 0 thì x^-1/2 bằng :

Hiển thị đáp án

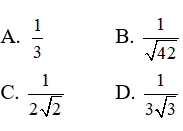
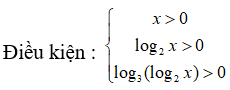
log₇(log₃(log₂x)) = 0 ⇔ log₃(log₂x) = 7⁰ = 1

⇔ log₂x = 3^t ⇔ x = 2³ = 8

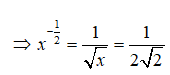
Chọn đáp án C

Câu 12: Giải phương trình logx = log(x + 3) - log(x - 1)

A. x = 1   B. x = 3   C. x = 4    D. x = -1, x = 3

Hiển thị đáp án

Điều kiện x > 1. Khi đó phương trình tương đương với

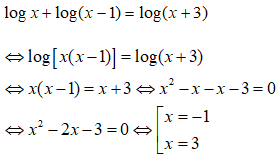
Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.

Chọn đáp án B.

Chú ý: Cũng như ở ví dụ 5, sai lầm học sinh dễ gặp bài này là do chủ quan muốn tiết kiệm thời gian mà quên đặt điều kiện, dẫn tới không loại được nghiệm x = -1 và chọn phương án nhiễu D.

Câu 13: Giải phương trình log_√2(x + 1) = log₂(x² + 2) - 1

A. x = 1   B. x = 0   C. x = 0, x = -4   D. x = 0, x = 1

Hiển thị đáp án

Điều kiện x > -1. Khi đó phương trình tương đương với

2log₂(x + 1) = log₂(x² + 2)

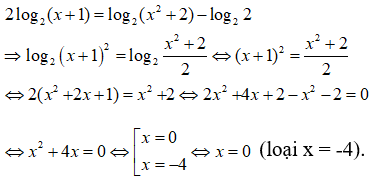
Chọn đáp án B

Câu 14: Cho biết log_b²x + log_x²b = 1, b > 0, b ≠ 1, x ≠ 1. Khi đó x bằng:

A. b    B. √b    C. 1/b     D. 1/b²

Hiển thị đáp án

Điều kiện: x > 0

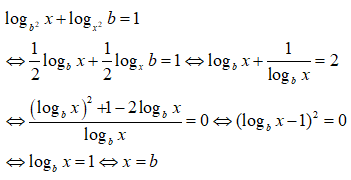
Chọn đáp án A.

Chú ý. Khác với các ví dụ trên, các biến đổi trong ví dụ này không làm mở rộng miền xác định của phương trình (x > 0). Do đó ta đã không nhất thiết phải đặt điều kiện x > 0. Trong nhiều trường hợp việc bỏ qua đặt điều kiện sẽ làm đơn giản hơn và tiết kiệm thời gian.

Câu 15: Cho biết 2^x = 8^{y + 1} và 9^y = 3^{x - 9} . Tính giá trị của x + y

A. 21     B. 18   C. 24    D. 27

Hiển thị đáp án

Vậy x + y =27.

Chọn đáp án D.

Câu 16: Giả sử x, y là hai số thực thỏa mãn đồng thời 3^{x2 - 2xy} = 1 và 2log₃x = log₃(y + 3). Tính x + y

A. 9/4     B. 3/2    C. 3   D. 9

Hiển thị đáp án

Điều kiện x > 0, y > -3.

Ta có: 3^{x2 - 2xy} = 1 = 3⁰ ⇔ x² - 2xy = 0

⇔ x(x - 2y) = 0 ⇔ x - 2y = 0 (x > 0) ⇔ x = 2y (1)

2log₃x = log₃( y + 3) ⇔ log₃x² = log₃(y + 3) ⇔ x² = y + 3 (2)

Thế (1) vào (2) ta được:

Câu 17: Giả sử α và β là hai nghiệm của phương trình 3 + 2log₂x = log₂(14x - 3). Khẳng định nào sau đây là đúng ?

A. α = -4    B. log₂α = -2    C. α = 3/2    D. α3/14

Hiển thị đáp án

Trước hết, ta giải phương trình 3 + 2log₂x = log₂(14x - 3) (1)

Điều kiện x > 3/14. Khi đó (1) <=7gt; log₂8 + log₂x² = log₂(14x - 3)

⇔ 8x² = 14x - 3 ⇔ = 8x² - 14x + 3 = 0

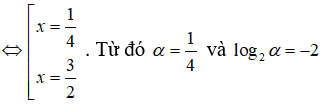
Câu 18: Tính tích các nghiệm của phương trình log_x4 + log₄x = 17/4

A. 1    B. 16    C. 4∜4   D. 256√2

Hiển thị đáp án

Điều kiện : x > 0 ; x ≠ 1

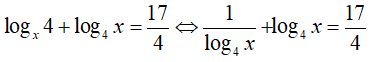
Đặt t = log₄x, nhận được phương trình:

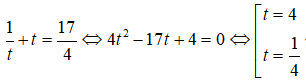
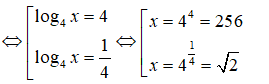
Tích hai nghiệm : 256.√2

Câu 19: Tìm hai số x và y đồng thời thỏa mãn 3^{x + y} = 81 và 81^{x - y} = 3

Hiển thị đáp án

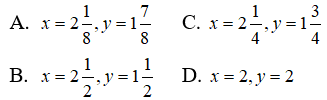
Câu 20: Một quần thể vi khuẩn bắt đầu từ 100 cá thể và cứ sau 3 giờ thì số cá thể lại tăng gấp đôi. Bởi vậy, số cá thể vi khuẩn được biểu thị theo thời gian t (tính bằng giờ) bằng công thức

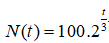
Hỏi sau bao lâu thì quần thể này đạt đến 50000 cá thể (làm tròn kết quả đến hàng phần mười) ?

A. 36,8 giờ   B. 30,2 giờ    C. 26,9 giờ    D. 18,6 giờ

Hiển thị đáp án

Sau t giờ thì số cá thể vi khuẩn có được là :

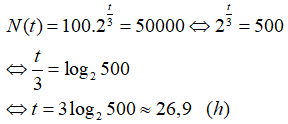
Câu 21: Khi đèn flash của một máy ảnh tắt thì ngay lập tức nguồn điện từ pin sẽ xạc cho tụ điện của nó. Lượng điện tích trong tụ xác định bởi công thức

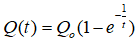
trong đó Q₀ là điện tích tối đa mà tụ có thể tích được, thời gian t tính bằng giây. Hỏi sau bao lâu thì tụ tích được 90% điện tích tối đa ?

A. 3,2 giây   B. 4,6 giây    C. 4,8 giây    D. 9,2 giây

Hiển thị đáp án

Để tụ tích được 90% điện tích tối đa thì Q(t) = 90%Q₀

Ta có: Q₀(1 - e^-1/2) = 0,9Q₀ ⇔ e^-1/2 = 0,1 ⇔ t = -2ln0,1 ≈ 4,6 (giây)

Câu 22: Chiều dài (tính bằng xentimet) của một loài cá bơn ở Thái Bình Dương theo tuổi của nó (kí hiệu là t, tính bằng năm) được ước lượng bởi công thức f(t) = 200(1 - 0,956e^-0,18t). Một con cá bơn thuộc loài này có chiều dài 140cm. Hãy ước lượng tuổi của nó.

A. 2,79 năm   B. 6,44 năm    C. 7,24 năm    D. 12,54 năm

Hiển thị đáp án

Con cá bơn có chiều dài là 140cm nên:

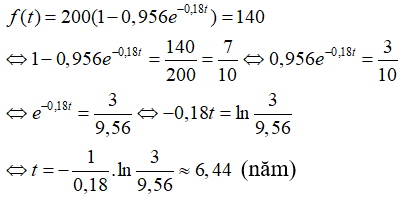
Câu 23: Có một dịch cúm trong một khu vực quân đội và số người lính ở đó mắc bệnh cúm sau t ngày (kể từ ngày dịch cúm bùng phát) được ước lượng bằng công thức

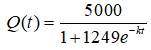
trong đó k là một hằng số. Biết rằng có 40 người lính mắc bệnh cúm sau 7 ngày. Tìm giá trị của hằng số k.

A. 0,33   B. 2,31    C. 1,31    D. -2,31

Hiển thị đáp án

Ta có:

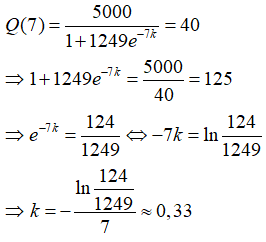
Câu 24: Nếu log(log(log(logx))) = 0 thì x = 10^k . Tìm giá trị của k

A. 10    B. 100    C. 10³    D. 10¹⁰

Hiển thị đáp án

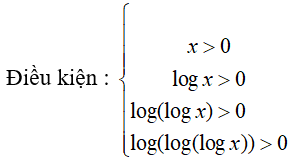
log(log(log(logx))) = 0 ⇔ log(log(logx)) = 1 ⇔ log(logx) = 10

⇔ logx = 10¹⁰ ⇔ x = 10¹⁰¹⁰ (thỏa mãn điều kiện)

⇒ k = 10¹⁰

Câu 25: Giải phương trình log₃x = (-2 + log₂100)(log₃√2)

A. x = 5    B. x = 3√2   C. x = 2⁴    D. x = 50

Hiển thị đáp án

Điều kiện : x > 0

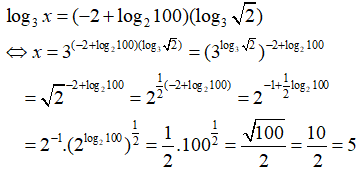
Câu 26: Tìm tập hợp các nghiệm của phương trình

Hiển thị đáp án

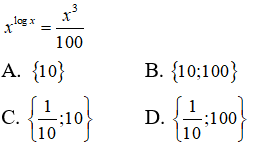
Lấy lôgarit cơ số 10 hai vế phương trình ta được

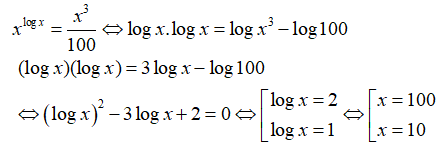
Kết hợp điều kiện, phương trình có 2 nghiệm là x= 100 và x= 10

Câu 27: Giả sử x₁, x₂ là hai nghiệm của phương trình 7^x + 2.7^{1 - x} - 9 = 0.

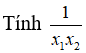
A. log₂7 + 1   B. log₇2 + 1    C. log₇2    D. log₂7

Hiển thị đáp án

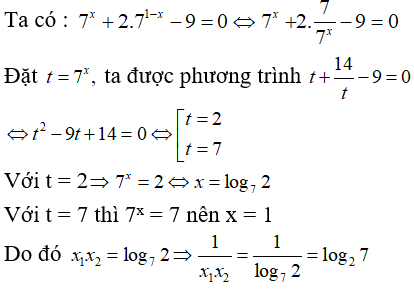
Câu 28: Tìm nghiệm của phương trình 4^{1 - x} = 3^{2x + 1}

Hiển thị đáp án

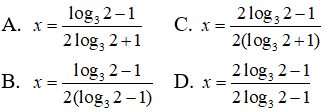
4^{1 - x} = 3^{2x + 1} ⇔ 2^{2 - 2x} = 3^{2x + 1}

Lấy lôgarit cơ số 3 hai vế ta được :

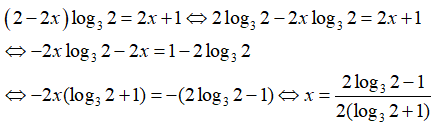
Câu 29: Giải phương trình log₅(x + 4) = 3

A. x = 11    B. x = 121    C. x = 239    D. x = 129

Hiển thị đáp án

Điều kiện : x + 4 > 0 ⇔ x > -4

PT ⇔ x + 4 = 5³ = 125 ⇔ x = 121 ( thỏa mãn điều kiện).

Vậy nghiệm cuả phương trình đã cho là 121.

Câu 30: Tìm các số thực a thỏa mãn log₁₀(a² - 15a) = 2

Hiển thị đáp án

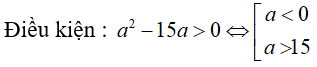
log₁₀(a² - 15a) = 2 ⇔ a² - 15a = 10² = 100 ⇔ a² - 15a - 100 = 0

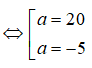
Câu 31: Giải phương trình x²lnx = lnx⁹

A. x = 3   B. x = ±3    C. x = 1, x = 3    D. x = 1, x = ±3

Hiển thị đáp án

Điều kiện x > 0.

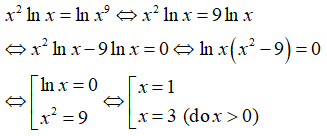
Câu 32: Giải phương trình log₄(log₃(log₂x)) = 0

A. x = 2    B. x = 8    C. x = ∛2    D. x = 4³²

Hiển thị đáp án

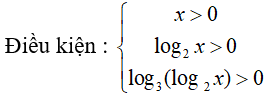
log₄(log₃(log₂x)) = 0 ⇔ log₃(log₂x) = 1 ⇔ log₂x = 3 ⇔ x = 2³ = 8 (thỏa mãn điều kiện).

Câu 33: Giải phương trình lnx + ln(x - 1) = ln2

A. x = 3/2    B. x = -1, x = 2    C. x = 2    D. x = 1, x = 3/2

Hiển thị đáp án

Điều kiện x > 1

Ta có: lnx + ln(x - 1) = ln2

⇔ x(x - 1) = 2 ⇔ x² - x - 2 = 0

⇔ x = -1 (loại) hoặc x = 2